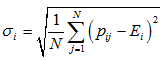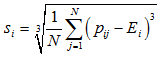数据挖掘实战——基于水色图像的水质评价

挖掘目的

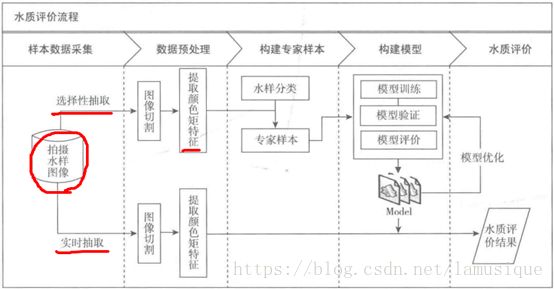
用数字图像处理部分来作为数据挖掘分析的数据源，按水色判断水质分类的数据以及用数码相机按照标准进行水色采集的图像数据，利用图像处理技术，通过水色图像实现水质的自动评价。

分析方法

水样图像维度过大，不易分析需要从中提取图像特征，提取反映图像本质的一些关键指标，这点在数据预处理中本质上是属性规约。属性一定程度上的关键直接影响识别效果和分类的好坏。

图像特征主要包括颜色特征、纹理特征、形状特征和空间关系特征等。与几何关系相比，颜色特征具有更好的区分度，表现为对周围环境以及物体的大小梯度均不敏感，鲁棒性高。到本次试验中，水色样本的颜色特征稳定性更好，所以主要关注颜色特征。博主对于图像是个小白，还是老老实实的去解释什么是颜色特征的吧？

颜色特征是一种全局特征，描述了图像或图像区域的表面性质，就是基于像素点的特征，图像呈现出来的色彩，每一个像素点都有各自的贡献。这种方法如今很成熟，处理识别分类有很多研究成果，主要采用颜色直方图和颜色矩方法。

颜色直方图——反映图像颜色的组成分布，即不同色彩在整幅图像的颜色出现概率，特别适用于描述那些难以自动分割的图像和要考虑物体空间位置的图像，缺点就是无法描述图像中颜色的局部分布及每种色彩的空间位置，即无法描述图像中的某一具体的对象或物体。

颜色矩——图像中的分布都可以用他的矩表示，根据概率论的理论，随机变量的概率分布可以由其各阶矩唯一的表示。一幅图像的色彩分布可认为是一种概率分布，那么图像可以由其各阶矩来描述。颜色矩包含各个颜色通道的一阶距、二阶距、三阶距，对于一个RGB颜色空间的图像，具有R G B三个颜色通道，则有9个分量。

1)     一阶颜色距

一阶颜色矩采用一阶原点矩，反映图像的整体明暗程度

                                              

其中，是在第i个颜色通道的一阶颜色矩，对于RGB颜色空间的图像，i=1,2,3，是第j个像素的第i个颜色通道的颜色值。

2)     二阶颜色距

二阶颜色矩采用的是二阶中心距的平方根，反映图像颜色的分布范围

                                                       

其中是在第i个颜色通道的二阶颜色矩，是在第i个颜色通道的一阶颜色矩

3)     三阶颜色距

三阶颜色矩采用的是三阶中心距的立方根，反映图像颜色分布的对称性

                                                       

其中是在第i个颜色通道的二阶颜色矩，是在第i个颜色通道的一阶颜色矩

本文考虑到颜色矩的特征分量相对于颜色直方图的特征量较少，遂采用基于颜色矩的方法。即建立水样图像与反映该图像特征的数据信息关系，同时由有经验的专家对水样图像根据经验分类，建立水样数据信息和水质类别的专家样本库，进而构建分类模型，得到水样图像与水质类别的映射关系，并经过不断调整系数优化模型，最后利用训练好的模型，自动判别出该水样的水质类别。

数据预处理

1.图像切割

为了提取水的特征，需要提取水样图像中央部分(101*101)具有代表意义的图像。[中心点左右距离50，上下距离50的矩阵块]

2.特征提取

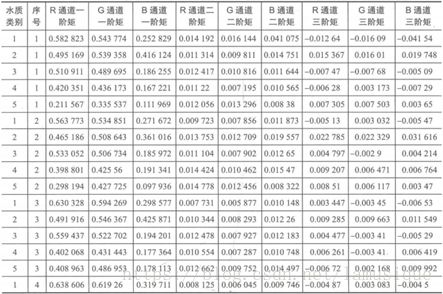
根据所提的颜色矩：一阶距二阶距三阶距。得到图像颜色特征如下所示：

3.模型构建

原样本随机抽样，以划分成80%训练样本和20%测试样本。本案例采用支持向量机作为水质评价分类模型。SVM模型python里面有相关的库支持，具体原理百度即可。

其中，1~9为输入的特征，我们发现特征的取值范围都在0~1之间，也就是说，如果直接输入SVM模型，彼此间的区分度会比较小。这时我们的常用处理方法——乘以1个k值，把数据间拉开，但是呢，k过大导致模型在训练样本中过拟合(如k=1000，在训练样本中准确率为100%，在测试样本中准确率不到20%)，k过小呢，又会导致区分度低，模型精确度差。因此只能根据测试准确率来选择k的最优值。

经过反复测试，本次建模中k的最优值大约为30.将特征值统一乘以30，然后建立支持向量机模型。

代码如下：

#构造特征和标签
x_train=data_train[:,2:]*30#放大特征
y_train=data_train[:,0].astype(int)#设置成int型
x_test=data_train[:,2:]*30#放大特征
y_test=data_train[:,0].astype(int)

#导入模型相关的函数，建立并训练模型
from sklearn import svm
model=snm.SVC()
model.fit(x_train,y_train)

import pickle
pickle.dump(model,open('../tmp/svm.model','wb'))
#最后一句保存模型，以后可以通过下面语句重新加载模型：
#model=pickle.load(open('../tmp/svm.model','rb'))

#导入输出相关的库，生成混淆矩阵
from sklearn import metrics
cm_train=metrics.confusion_matrix(y_train,model.predict(x_train))#训练样本的混淆矩阵
cm_test=metrics.confusion_matrix(y_test,model.predict(x_test))#测试样本的混淆矩阵

#保存结果
pd.DataFrame(cm_train,index=range(1,6),columns=range(1,6)).to_excel(outputfile1)
pd.DataFrame(cm_test,index=range(1,6),columns=range(1,6)).to_excel(outputfile2)

4.训练结果分析

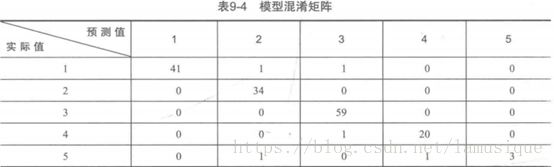
建立模型后，利用训练样本进行回判，得到的混淆矩阵如下（中间的表示预测与实际正确），分类结果为96.91%。

5.水质评价

针对测试样本我们进行评价，代入已构建好的支持向量机模型，得到的测试样本的混淆矩阵如下。准确率达95.12%，说明水质分析的还不错，方法可靠。

总结：最大的收获就是明白了图像的颜色特征——颜色矩，并构造。简明实用。

至于其他书上是这么说的。