数据结构与算法学习笔记——动态规划的入门与编程实现

本文的内容部分引自：
http://hawstein.com/posts/dp-novice-to-advanced.html

前言

我们遇到的问题中，有很大一部分可以用动态规划(简称DP)来解。 解决这类问题可以很大地提升你的能力与技巧，我会试着帮助你理解如何使用DP来解题。 这篇文章是基于实例展开来讲的，因为干巴巴的理论实在不好理解。

简介

动态规划算法通常基于一个递推公式及一个或多个初始状态。 当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度， 因此它比回溯法、暴力法等要快许多。
现在让我们通过一个例子来了解一下DP的基本原理。
首先，我们要找到某个状态的最优解，然后在它的帮助下，找到下一个状态的最优解
即大问题转化成小问题，而小问题与大问题同质

实例1

如果我们有面值为1元、3元和5元的硬币若干枚，如何用最少的硬币凑够11元？ (表面上这道题可以用贪心算法，但贪心算法无法保证可以求出解，比如1元换成2元的时候)

好了，让我们从最小的i开始吧。
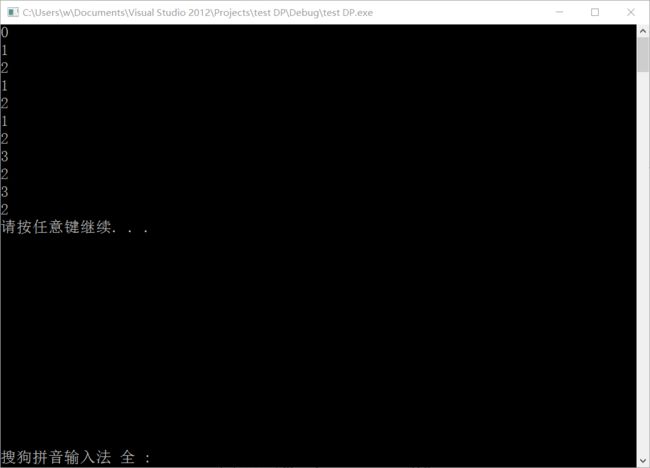
当 i=0 ，即我们需要多少个硬币来凑够0元。 由于1，3，5都大于0，即没有比0小的币值，因此凑够0元我们最少需要0个硬币。 (这个分析很傻是不是？别着急，这个思路有利于我们理清动态规划究竟在做些什么。) 这时候我们发现用一个标记来表示这句“凑够0元我们最少需要0个硬币。”会比较方便， 如果一直用纯文字来表述，不出一会儿你就会觉得很绕了。那么， 我们用 d(i)=j 来表示凑够i元最少需要j个硬币。于是我们已经得到了 d(0)=0 ， 表示凑够0元最小需要0个硬币。
当 i=1 时，只有面值为1元的硬币可用， 因此我们拿起一个面值为1的硬币，接下来只需要凑够0元即可，而这个是已经知道答案的， 即 d(0)=0 。所以，

d(1)=d(1−1)+1=d(0)+1=0+1=1

当 i=2 时， 仍然只有面值为1的硬币可用，于是我拿起一个面值为1的硬币， 接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量)，而这个答案也已经知道了。 所以

d(2)=d(2−1)+1=d(1)+1=1+1=2

一直到这里，你都可能会觉得，好无聊， 感觉像做小学生的题目似的。因为我们一直都只能操作面值为1的硬币！耐心点， 让我们看看i=3时的情况。

当 i=3 时，我们能用的硬币就有两种了：1元的和3元的( 5元的仍然没用，因为你需要凑的数目是3元！5元太多了亲)。 既然能用的硬币有两种，我就有两种方案。如果我拿了一个1元的硬币，我的目标就变为了： 凑够3-1=2元需要的最少硬币数量。即

d(3)=d(3−1)+1=d(2)+1=2+1=3

这个方案说的是，我拿3个1元的硬币；第二种方案是我拿起一个3元的硬币， 我的目标就变成：凑够3-3=0元需要的最少硬币数量。即

d(3)=d(3−3)+1=d(0)+1=0+1=1

这个方案说的是，我拿1个3元的硬币。好了，这两种方案哪种更优呢？ 记得我们可是要用最少的硬币数量来凑够3元的。所以， 选择 d(3)=1 ，怎么来的呢？

具体是这样得到的：

d(3)=min{d(3−1)+1,d(3−3)+1}

所以得到的状态转移方程是：

d(i)=min{d(i−vj)+1}

其中 i−vj>=0 ， vj 表示第 j 个硬币的面值；

实例1程序实现与结果

#include
#include
#include

using namespace std;

int _tmain(int argc, _TCHAR* argv[])
{
    vector<int> num;
    num.push_back(0);
    int v[3]={1,3,5};
    for(int i=1;i<11;i++)
    {
        vector<int> num2;
        for(int j=0;j<3;j++)
        {
            if(i-v[j]>=0)
            {
                num2.push_back(num[i-v[j]]+1);
            }
        }
           sort(num2.begin(),num2.end());
           num.push_back(num2[0]);

    }
    for(int i=0;icout<"pause");
    return 0;
}

与数学分析结果的对比：

上面讨论了一个非常简单的例子。现在让我们来看看对于更复杂的问题， 如何找到状态之间的转移方式(即找到状态转移方程)。 为此我们要引入一个新词叫递推关系来将状态联系起来(说的还是状态转移方程)
OK，上例子，看看它是如何工作的。

实例2

一个序列有N个数： A[1],A[2],…,A[N] ，求出最长非降子序列的长度。
为了方便理解我们是如何找到状态转移方程的，我先把下面的例子提到前面来讲。 如果我们要求的这N个数的序列是：

5，3，4，8，6，7

根据上面找到的状态，我们可以得到：（下文的最长非降子序列都用LIS表示）
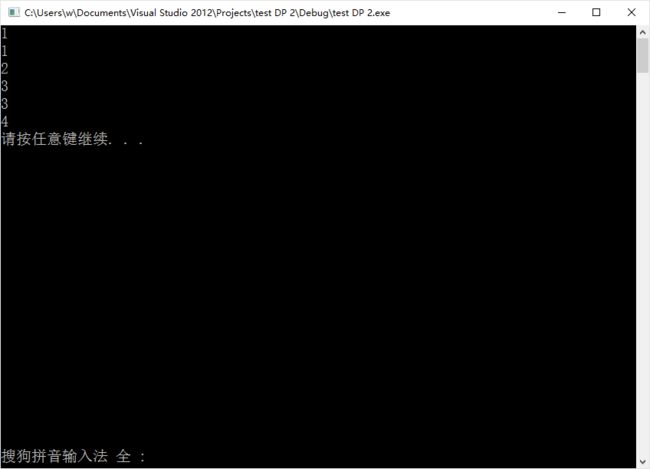
•前1个数的LIS长度 d(1)=1 (序列：5)
•前2个数的LIS长度 d(2)=1 (序列：3；3前面没有比3小的)
•前3个数的LIS长度 d(3)=2 (序列：3，4；4前面有个比它小的3，所以d(3)=d(2)+1)
•前4个数的LIS长度 d(4)=3 (序列：3，4，8；8前面比它小的有3个数，所以 d(4)=max{d(1),d(2),d(3)}+1=3

OK，分析到这，我觉得状态转移方程已经很明显了，如果我们已经求出了d(1)到d(i-1)， 那么d(i)可以用下面的状态转移方程得到：

d(i)=max{1,d(j)+1},其中j<i,A[j]<=A[i]

用大白话解释就是，想要求d(i)，就把i前面的各个子序列中， 最后一个数不大于A[i]的序列长度加1，然后取出最大的长度即为d(i)。 当然了，有可能i前面的各个子序列中最后一个数都大于A[i]，那么d(i)=1， 即它自身成为一个长度为1的子序列。

实例2程序实现与结果

#include "stdafx.h"
#include
#include
#include

using namespace std;

int _tmain(int argc, _TCHAR* argv[])
{
    int seq[6]={5,3,4,8,6,7};
    vector<int> num;
    //num.push_back(1);
    for(int i=0;i<6;i++)
    {
        vector<int> num2;
        num2.push_back(1);
        for(int j=0;jif(seq[j]<=seq[i])
                num2.push_back(num[j]+1);
        }
        sort(num2.begin(),num2.end());
        num.push_back(num2[num2.size()-1]);
    }
    for(int j=0;jcout<"pause");
    return 0;
}

与数学分析结果的对比：

由于博主的学识有限，难免会出现错误，欢迎大家在评论区批评，指正，交流，也欢迎大家对博文的内容上的继续补充