递归算法中的超时问题解决方法

一、前言

数据结构里边，在经典的树的前中后序遍历、斐波那契数列问题中，我们使用递归实现，简单明了。然而前者使用了大量的栈内存，后者包含大量的重复计算，因此效率极低。这种思想，应用到算法问题解决中，会不可避免地出现超时现象。

如何保证简洁明了的同时，提高效率呢？

二、解决方法

下面以经典的斐波那契数列为例，给出各类通用的解决方案，使用算法主流语言 Python 实现：

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368…

def fib1(n: int):
    if n <= 2:
        return 1
    return fib1(n - 1) + fib1(n - 2)

结果：当 n = 40 时，时间 10s 过去了，结果还没计算出来（超时）
原因：太多重复计算

1.记忆化搜索

改进1：使用一个数组，存放曾经计算过的结果，下次遇到同样的计算，直接获取结果。

def fib2(n: int):
    if n <= 2:
        return 1
    memo = [-1] * n
    memo[0] = memo[1] = 1
    for i in range(2, n):
        memo[i] = memo[i - 1] + memo[i - 2]
    return memo[n - 1]

结果1：去除了常规递归写法的重复计算，没有超时，但占用O(n)的内存空间。

2.缓存

改进2：缓存每次新计算的结果，不要一上来，就申请O(n)的空间。

from functools import lru_cache
@lru_cache(10 ** 8)
def fib3(n: int):
    if n <= 2:
        return 1
    return fib3(n - 1) + fib3(n - 2)

结果2：效果和1中的差不多，但思路和常规递归一样清晰，空间占用稍少。

这里使用了 Python 语言，一个注解就解决了问题，简直开了挂。
但自己实现也不难，Python 可以使用一个字典来缓存计算结果，Java可有使用一个 HashMap 来缓存计算结果，都可以达到同样的效果。

3.递推

改进3：使用两个变量，存储计算的结果即可，一直往后递推

def fib4(n: int):
    if n <= 2:
        return 1
    a, b = 1, 1
    for _ in range(2, n):
        a, b = b, a + b
    return b

结果3：省内存、省时间，但是不是那么通用。

三、实战

下面以一道清华大学计算机考研复试上机题为例 —— 递推数列 ，演示秒杀绝技 ~

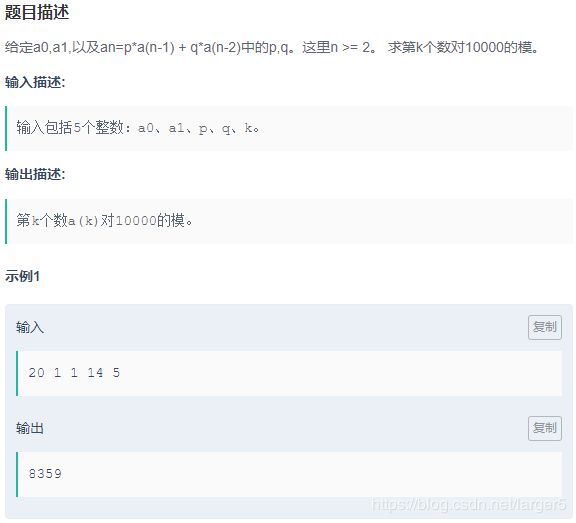
a0, a1, p, q, k = map(int, input().split())

from functools import lru_cache


@lru_cache(10 ** 8)  # 没有加上，为上图结果，加上，为下图结果
def get(n: int):
    if n == 0:
        return a0
    if n == 1:
        return a1
    return p * get(n - 1) % 10000 + q * get(n - 2) % 10000


print(get(k) % 10000)

很多网友都使用记忆化搜索来解决，思路错综复杂，代码凌乱不堪 ~

四、小结

生活问题解决上，推荐使用注解式缓存的解决方法，因其他算法，需要再常规思路的基础上，做小规模的修改，而注解式缓存，只是在常规递归的基础上，加一个注解（或者自行hash）就完事了，且为通法。

至于项目中，则要具体情况，考虑时间复杂度、空间复杂度的最优解。