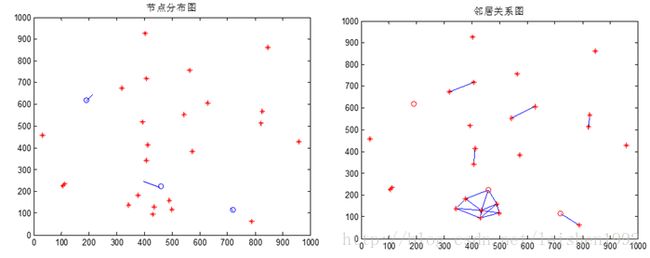
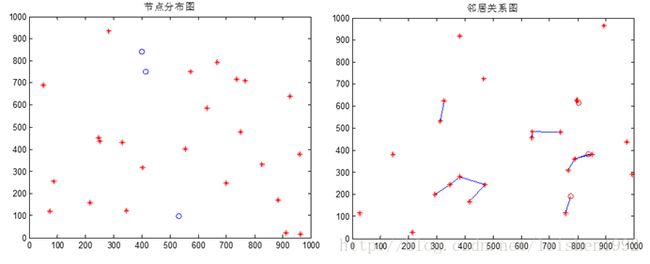
欢迎使用CSDN-markdown编辑器

列车高速定位系统的测试与仿真

---

1.引言

伴随着国民经济的飞速发展，人们对于轨道交通便利和安全的需求程度变得越来越高。轨道交通作为陆地的高密度载客交通工具，在我国的长距离运输体系中占据了无比重要的地位。但是随着列车的速度越来越快，种类越来越多，对于列车的安全监控技术就显得尤为重要。其中，定位技术作为一种重要的列车状态监控手段，也越来越受学术界的关注。由于列车行驶途径上环境的复杂性，获取列车的定位参数的准确性和实时性存在一定的难度。GPS作为一种低成本、易维护的定位技术手段，可以很好的满足列车在多种环境下的定位。
为了测试GPS技术对于列车定位的效果，本文首先介绍了几种传统的列车定位手段，综合比较了他们的优劣势，确定了GPS定位技术的优越之处。进而对GPS定位的信号构成、定位系统组成、定位原理以及在列车定位系统上的应用都做出了简介。基于此，将GPS系统等价为数个无线传感网络，并结合APIT定位算法和RAPIT定位算法，使用Matlab对其定位效果进行了仿真，仿真结果显示了使用RAPIT定位算法模拟GPS定位具有更好的准确性。
此外，为了估算信号传输过程的损耗，使列车的移动定位系统更加精准，本文采用了传统的Hata信道损耗估计算法和最小二乘法对列车的信号传输损耗状态进行了评估。在分析了Hata算法和最小二乘法的基础上，使用Matlab对这两种算法在城市环境下评估列车的信道损耗模拟进行了对比，仿真结果显示了最小二乘法在评估列车信道损耗的过程比起Hata算法更具优越性。

2.GPS列车定位的仿真

在现实世界中，我们通常使用的GPS体系是由围绕地球运转的24个卫星构成的，在算法上可以被模拟为24个接收节点来处理。也就是说，可以将整个GPS定位体系模拟成由24个信号节点构成的无线传感系统来进行模拟仿真。这里我们应用RAPIT这种结合了APIT和RSSI这两种经典的区域无线网络定位算法来进行GPS定位模拟。
## APIT算法与RSSI算法概述 ##

2.1. APIT
作为一种传统的传感网咯的定位算法，APIT算法在无线传感器网络定位体系中占据了非常重要的地位。APIT算法是一种使用三角形逼近的一种拟合式算法，在它的计算过程之中，不需要距离参数，而需要通信节点的区域参数来进行被测通信节点的位置参数。 ，其实现方法相对简单，定位所需的成本消耗也比较的低，此外由于它在定位计算法过程之中不需要距离参数，所以对于测量设备的功耗以及计算精度的需求相对较低，因而被广泛地运用在WIFI、ZigBee、Bluetooth等无线传感网络体系组建的的定位设备之中。其基本思想是利用众多的通信节点中的三个具有收法信号功能的通信节点组成一个三角形，进而通过区域测量的方法来区别被测的通信节点的位置是在这个三角形之内还是在三角形所覆盖区域的外面。如果在三角形内，则将其标记，依次 测量用通信节点进行 ，最终通过多次这样的区域逼近拟合算法来得到一个最小的三角形区域，再通过计算这个三角形的重心所在位置以作为被测通信节点的位置坐标参数。算法原理见图1。该算法的基本理论依据是最佳三角形内点测试法(PIT)，如图4.1所示：

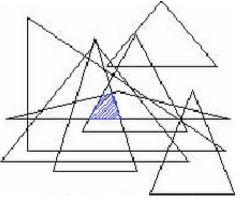
图4.1 APIT算法原理
APIT算法在进行定位之前，首先要明确未知节点M是否处于已知的三个锚节点所连成的三角形内。因此，对于随机分布在某区域内的无线传感器网络，在需要确定位置信息的未知节点M的无线射程范围内随机选取三个（或三个以上，这里以三个定位节点做说明)已知位置信息的定位节点： ，确定未知位置M是否在几个定位节点围成的图形之内（这里是 )。将M点向任意一个方向移动，如果节点M至少与定位节点A、B、C任何一个接近或者原理，则表明点M处于 之内，如图4.2(a)所示；反之，如果M点在进行位移的时候与另外三个定位节点的距离同时出现了拉远或者靠近的状况，则表明M目前处于 所涵盖的范围之外，如图4.2(b)所示：

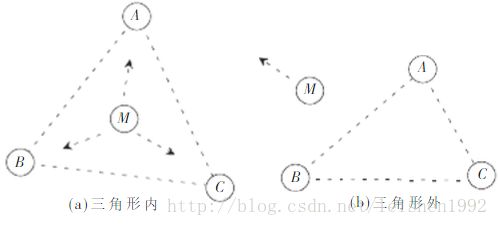
图4.2 APIT计算过程原理
现在假定在一片通信状况理想的区域之内有n个用于定位的通信传感器节点 ，其位置坐标分别为 。未知点M的估计坐标为 。设每个定位节点到未知位置点M的信号强度分别为 。则通过APIT算法可以得到定位节点 对节点M的限定距离为：
(2.6)
得到节点M一定在以 为圆心， 为半径的圆形区域之内，也一定在 以其限定距离为半径的圆的重叠区域之内。
但是在随机布置的传感器网络中,可能有一些节点(比如M节点)侦听到的锚节点个数小于3，则这些节点无法进行APIT测试，也就无法判断其位置,为第一类误差情况。另外，可能有一些节点(比如M节点)因为位置原因,尽管接收到的定位节点个数大于等于三个，但是却仍然无法判断其位置，为第二类误差情况.如图4.3所示：

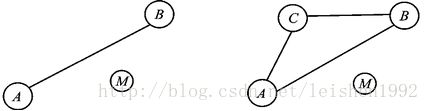
图4.3 APIT的两种误差情况

2.2. RSSI
所谓RSSI算法就是普遍所说的质心定位算法，它是基于多传感器网络的一种几何上的定位方法。在RSSI ，根据实际应用状况的不同，有着许多的衍生和变形算法，其中，质心定位的方法与APIT的三角形拟合算法比较的相似，同时在软件上相对易于实现，但是由于RSSI算法本身是通过圆形进行重心计算法的一种定位方法，所以在同等条件下进行未知通信节点的位置坐标定位的时候，这种质心定位算法的定位效果相较于区域拟合的APIT算法就相形见绌了。基于RSSI的质心定位算法的核心思想如下所示：在各个传感器节点的通信范围内，待定 至少三个信标节点发送的带有自身位置信息和RSSI值的通信信号；未知的通信节点利用RSSI值来确定它与对应的测量用通信设备之间的实际家怒江，在通过一系列的计算就可以得到三个距离数据。接下来分别以这三个测量用的通信设备作为圆心，以及上述方法测得的距离作为半径画三个圆，由于设备本身存在的固定误差和测量过程中的自然因素和非自然因素的影响，这三个圆必定不能交于一点，如图4.4所示：

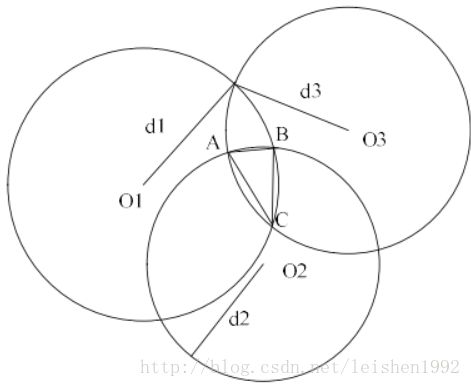
图2.4 基于RSSI的质心定位算法
求出三个相交的点的坐标，再求出三角形ABC的质心，也就是被测的通信点的一个估计坐标。设上述三个圆的圆心坐标分别为 ，他们的半径分别为 ，则圆的方程组如式4.1所示：
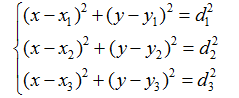(4.1)

## APIT算法与RSSI仿真 ##

仿真结果：

部分代码：

%hata 模型函数
function pathloss= hata(distance, frequency, hte, hre, type)

% pathloss= hata(distance, frequency, hte, hre, type) 

% 参数解释
% pathloss     : 路径损耗值，一维矩阵，对应不同距离抽样

% distance  : 发射机与接受机之间的距离，以一维矩阵表示，包含多个测量距离抽样值

% frequency : 载波频率，范围[150,1500] MHz


if type == 1
  pathloss= hata_urban1(distance, frequency, hte, hre);
elseif type == 2
  pathloss= hata_urban2(distance, frequency, hte, hre);
elseif type == 3
  pathloss= hata_suburban(distance, frequency, hte, hre);
else
  pathloss= hata_rural(distance, frequency, hte, hre);
end

% 仿真程序
% 使用m文件 :hata.m
% function pathloss= hata(distance, frequency, hte, hre, type)

% 参数解释
% pathloss     :路径损耗值，一维矩阵，对应不同距离抽样

% distance  :  发射机与接受机之间的距离(m)，以一维矩阵表示，包含多个测量距离抽样值

% frequency :  载波频率，范围[150,1500] MHz

% hte :        发射天线有效高度，范围[30, 200] (m)

% hre        : 接受天线有效天线，范围 [1, 10] (m)

% type       : 地理类型
%              1 - 中小城市
%              2 - 大城市
%              3 - 郊区
%              4 - 农村地区.
clc;clear;
hold off;
d=10:10:1000;  % 距离0~1000m之间抽样  步长10m
dkm=d/1000;     % 换算成千米
para=[900 100 2;  900 200 2;  600 100 2]; %函数参数，分三组数据如下
                                          %第一组： fc=900MHz,hte=100m,hre=2m
                                          %第二组： fc=900MHz,hte=200m,hre=2m
                                          %第三组： fc=600MHz,hte=100m,hre=2m
style=['-b' '--y' '-.'];
 for i=1:1          % 三组数据
         pl=hata(dkm,para(i,1),para(i,2),para(i,3),2);   % 第t种地理类型 第i组数据得到的路径损耗值    
        %pl=hata(dkm,900,100,2,t);   % 第t种地理类型 第i组数据得到的路径损耗值    

         %semilogy(d,pl);
         plot(d,pl);

 end
 xlswrite('hatadata.xls',pl);
 % 计算不同地理类型下的路径损耗值并绘图
  for t=1:4              % 4种地理类型
     for i=1:1          % 三组数据
          pl=hata(dkm,para(i,1),para(i,2),para(i,3),t);   % 第t种地理类型 第i组数据得到的路径损耗值    
         %pl=hata(dkm,900,100,2,t);   % 第t种地理类型 第i组数据得到的路径损耗值    

          %semilogy(d,pl);
          plot(d,pl);
          hold  on;
      end
          % end
  end