一些基本数字图像处理算法
一些基本数字图像处理算法
版权声明:本文为原创文章,未经博主允许不得用于商业用途。
所有的图像算法都在DIPAlgorithm类中,并且所有算法都为抽象成员函数。我已经按照java注释规范为所有方法添加使用说明注释,具体实现可见于DIPAlgorithm.java,这里只做算法说明。
1 图像扭曲

模仿PS的扭曲功能,通过建立一个三角形映射网格实现对图像的扭曲。
如上图,一共设置了45个控制点围成74个三角形网格
扭曲即形变处理其实是寻找一个函数,以所有网格顶点原始坐标为输入,扭曲后所有网格顶点坐标为输出。为了简化计算任务,采用控制栅格插值方法,对每个三角网格独立计算映射关系,如下图:
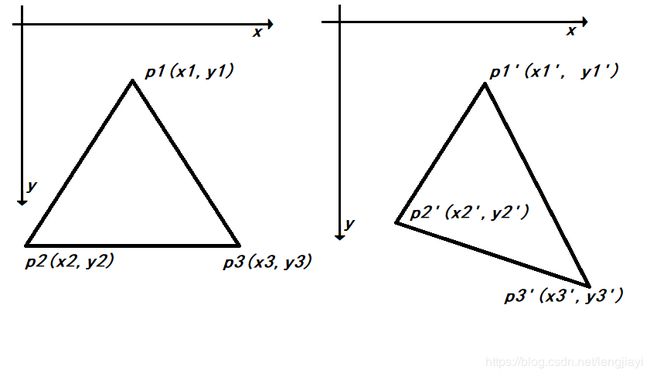
即求解矩阵 M M M满足 M A = B MA = B MA=B,其中 A A A为原顶点的齐次矩阵:
A = [ x 1 y 1 1 x 2 y 2 1 x 3 y 3 1 ] A = \begin{bmatrix} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \\ \end{bmatrix} A=⎣⎡x1x2x3y1y2y3111⎦⎤
B为形变后顶点的其次矩阵:
B = [ x 1 ′ x 2 ′ x 3 ′ y 1 ′ y 2 ′ y 3 ′ ] B = \lbrack\begin{matrix} x_{1}^{'} & x_{2}^{'} & x_{3}^{'} \\ y_{1}^{'} & y_{2}^{'} & y_{3}^{'} \\ \end{matrix}\rbrack B=[x1′y1′x2′y2′x3′y3′]
M即为 2 × 3 2 \times 3 2×3的映射矩阵,且由于三角形三点不共线,因此A为可逆阵,
M = B A − 1 M = BA^{- 1} M=BA−1
对于三角形中的点 p ( x , y ) p\left( x,\ y \right) p(x, y),其映射后坐标 p ′ = M [ x y 1 ] p^{'} = M\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} p′=M⎣⎡xy1⎦⎤
2 直方图计算
直方图计算实际上即求图像的概率密度函数PDF,只需遍历一次所有像素点即可获得。
3 直方图均衡化算法
对于连续图像直方图均衡化其实是种点运算f,
对不同灰度值做映射,使得所有像素频率相等。
对于点运算f,有如下性质:
D B = f ( D A ) , H B ( D B ) Δ D B = H A ( D A ) Δ D A D_{B} = f\left( D_{A} \right),\ H_{B}\left( D_{B} \right)\Delta D_{B} = H_{A}\left( D_{A} \right)\Delta D_{A} DB=f(DA), HB(DB)ΔDB=HA(DA)ΔDA
其中D为灰度值,H即为灰度值在图像中的频数,整理可得
H B ( D B ) = H A ( D A ) Δ D A Δ D B = H A ( D A ) Δ D B Δ D A = H A ( D A ) d D B d D A H_{B}\left( D_{B} \right) = \frac{H_{A}\left( D_{A} \right)\Delta D_{A}}{\Delta D_{B}} = \frac{H_{A}\left( D_{A} \right)}{\frac{\Delta D_{B}}{\Delta D_{A}}} = \frac{H_{A}\left( D_{A} \right)}{\frac{dD_{B}}{dD_{A}}} HB(DB)=ΔDBHA(DA)ΔDA=ΔDAΔDBHA(DA)=dDAdDBHA(DA)
= H A ( D A ) f ′ ( D A ) = H A ( f − 1 ( D B ) ) f ′ ( f − 1 ( D B ) ) = \frac{H_{A}\left( D_{A} \right)}{f'(D_{A})} = \frac{H_{A}\left( f^{- 1}\left( D_{B} \right) \right)}{f'(f^{- 1}(D_{B}))} =f′(DA)HA(DA)=f′(f−1(DB))HA(f−1(DB))
即:
寻找函数f使得 H B ( D ) H_{B}(D) HB(D)为常数 A 0 D m , A 0 , D m \frac{A_{0}}{D_{m}},A_{0},D_{m} DmA0,A0,Dm。
由(1)可知,KaTeX parse error: Expected 'EOF', got '\ ' at position 58: …\right)}{f'(D)}\̲ ̲\Rightarrow f^{…
即 f ( D ) = D m C D F ( D ) f\left( D \right) = D_{m}CDF(D) f(D)=DmCDF(D),CDF即累积分布函数
因此只需求得直方图的前序和即可获得映射关系。
4 图像灰度化
目前比较符合人眼的灰度化权重为0.299、0.578和0.114,为了加速计算使用近似公式 D = ( 3 r + g + 6 b ) / 10 D = (3r + g + 6b)/10 D=(3r+g+6b)/10
5 图像二值化
我使用的二值化算法为OSTU大律二值化算法。二值化操作即利用分割阈值u,将图片分为前景后景两部分。OSTU大律法认为使得前景像素和背景像素灰度方差g最大的阈值即为最佳分割阈值。
g = w 0 w 1 ( u 0 − u 1 ) 2 g = w_{0}w_{1}\left( u_{0} - u_{1} \right)^{2} g=w0w1(u0−u1)2
其中 w 0 , w 1 w_{0},\ w_{1} w0, w1为前景、后景在图像中的比例,KaTeX parse error: Expected 'EOF', got '\ ' at position 7: u_{0},\̲ ̲u_{1}为前景、后景的平均灰度。
在实现时,只需遍历所有灰度,利用CDF求出每种灰度的方差,取最大者作为阈值即可。
6 前景分离
目前主流的前景分离为深度学习算法。这里只使用了最基本的阈值分离法,分别为RGB三个通道设置不同阈值,将小于阈值的像素作为背景,大于阈值的作为前景。
7 滤波
我使用的滤波方法是高斯滤波和中值滤波,高斯滤波即使用二维高斯函数作为滤波函数,中值滤波即使用邻域的中位数作为滤波函数。
高斯滤波器为线性滤波器,可以有效消除高斯噪声。由于高斯函数离中值越近权重越大,因此相对于均值滤波器更加柔和,对边缘的保留效果更好。这里我使用的是如下矩阵做卷积:
[ 1 2 3 2 1 2 4 6 4 2 3 6 7 6 3 2 4 6 4 2 1 2 3 2 1 ] \begin{bmatrix} 1 & 2 & 3 & 2 & 1 \\ 2 & 4 & 6 & 4 & 2 \\ 3 & 6 & 7 & 6 & 3 \\ 2 & 4 & 6 & 4 & 2 \\ 1 & 2 & 3 & 2 & 1 \\ \end{bmatrix} ⎣⎢⎢⎢⎢⎡1232124642367632464212321⎦⎥⎥⎥⎥⎤
中值滤波器为非线性滤波器,可以有效的去除椒盐噪声和斑点噪声并且不会使图像变模糊。
8 形态学扩张和腐蚀
形态学腐蚀可记为 AΘB \text{AΘB} AΘB,其中A为输入图像,B为结构单元。对于二值图像,当且仅当当前像素点满足腐结构单元时才会被保留。对于灰度图像,则可类比为最小值,即
f Θ b ( x , y ) = m i n { f ( x − x ′ , y − y ′ ) − b ( x ′ , y ′ ) ∣ ( x ′ , y ′ ∈ D b ) } f\Theta b\left( x,y \right) = min\{ f\left( x - x^{'},\ y - y^{'} \right) - b(x^{'},y')|(x^{'},y^{'} \in D_{b})\} fΘb(x,y)=min{f(x−x′, y−y′)−b(x′,y′)∣(x′,y′∈Db)}
形态学扩张可看作腐蚀的逆操作,记作 A ⨁ B A\bigoplus B A⨁B,对于二值图像,将每个有效像素点的邻域结构单元置1,对于灰度图像则取最大值,即
f ⨁ b ( x , y ) = m a x { f ( x − x ′ , y − y ′ ) − b ( x ′ , y ′ ) ∣ ( x ′ , y ′ ∈ D b ) } f\bigoplus b\left( x,y \right) = max\{ f\left( x - x^{'},\ y - y^{'} \right) - b(x^{'},y')|(x^{'},y^{'} \in D_{b})\} f⨁b(x,y)=max{f(x−x′, y−y′)−b(x′,y′)∣(x′,y′∈Db)}
本程序将结构单元b统一设定为5*5矩形。
通过扩张和腐蚀的结合可实现结构开运算( A o B = ( AΘB ) ⨁ B AoB = \left( \text{AΘB} \right)\bigoplus B AoB=(AΘB)⨁B)和结构闭运算( A o B = ( A ⨁ B ) ΘB AoB = \left( A\bigoplus B \right)\text{ΘB} AoB=(A⨁B)ΘB)对图像进行粗化、细化、滤波等处理
9 傅里叶变换和滤波
变换公式
傅里叶变换可以将信号从时域转换到频域,因此可以看出许多时域中不明显的特征。二维傅里叶变换(CFT)公式如下:
F ( u , v ) = ∬ f ( x , y ) e − 2 π j → ( u x + v y ) dxdy F\left( u,v \right) = \iint_{}^{}{f\left( x,y \right)e^{- 2\pi\overrightarrow{j}(ux + vy)}}\text{dxdy} F(u,v)=∬f(x,y)e−2πj(ux+vy)dxdy
其中 j → 2 = − 1 , f , F {\overrightarrow{j}}^{2} = - 1,f,F j2=−1,f,F,同样二维傅里叶逆变换公式如下:
f ( x , y ) = ∬ F ( u , v ) e 2 π j → ( u x + v y ) dudv f\left( x,y \right) = \iint_{}^{}{F\left( u,v \right)e^{2\pi\overrightarrow{j}(ux + vy)}}\text{dudv} f(x,y)=∬F(u,v)e2πj(ux+vy)dudv
对于离散函数,可以定义离散二维傅里叶变换(DFT)和逆变换:
G ( m , n ) = 1 MN ∑ 0 ≤ i ≤ M − 1 0 < k < N − 1 g ( i , k ) e − 2 π j → ( im M + jn N ) G\left( m,n \right) = \frac{1}{\sqrt{\text{MN}}}\sum_{\begin{matrix} 0 \leq \ i\ \leq \ M - 1 \\ 0 < k < N - 1\ \\ \end{matrix}}^{}{g\left( i,k \right)e^{- 2\pi\overrightarrow{j}(\frac{\text{im}}{M} + \frac{\text{jn}}{N})}} G(m,n)=MN10≤ i ≤ M−10<k<N−1 ∑g(i,k)e−2πj(Mim+Njn)
g ( i , k ) = 1 MN ∑ 0 ≤ m ≤ M − 1 0 < n < N − 1 g ( m , n ) e 2 π j → ( im M + jn N ) g\left( i,k \right) = \frac{1}{\sqrt{\text{MN}}}\sum_{\begin{matrix} 0 \leq \ m\ \leq \ M - 1 \\ 0 < n < N - 1\ \\ \end{matrix}}^{}{g\left( m,n \right)e^{2\pi\overrightarrow{j}(\frac{\text{im}}{M} + \frac{\text{jn}}{N})}} g(i,k)=MN10≤ m ≤ M−10<n<N−1 ∑g(m,n)e2πj(Mim+Njn)
DFT可以理解为对连续二维信号进行了频率为M,
N的采样,之后通过计算其和频域空间M*N个基向量的相关性(在该方向投影)将时域信号映射到频域。iDFT可以理解为通过M*N个基向量合成原始时域信号。
矩阵表示
傅里叶变换实际上是一种线性变换,因此在实际计算中常常将 g g g扩充为 N ∗ N N*N N∗N方阵,此时DFT可以通过矩阵表示: G = W − 1 g W , W ik = 1 N e 2 π j → ik N G = \mathcal{W}^{- 1}g\mathcal{W},\mathcal{W}_{\text{ik}} = \frac{1}{N}e^{2\pi\overrightarrow{j}\frac{\text{ik}}{N}} G=W−1gW,Wik=N1e2πjNik。
易知 W ik = W ki \mathcal{W}_{\text{ik}} = \mathcal{W}_{\text{ki}} Wik=Wki,且为正交矩阵,因此 W \mathcal{W} W为酉矩阵,即 W − 1 = ( W ∗ ) T = W ∗ \mathcal{W}^{- 1} = \left( \mathcal{W}^{*} \right)^{T} = \mathcal{W}^{*} W−1=(W∗)T=W∗, G = W ∗ g W G = \mathcal{W}^{*}g\mathcal{W} G=W∗gW,其中 F ∗ F F^{*}F F∗F。
由于傅里叶变换为酉变换,即 W t = W − 1 \mathcal{W}^{t} = \mathcal{W}^{- 1} Wt=W−1
图像的傅里叶变换
对于二维图片可以看作二维矩阵,因此可以进行DFT。二维图片经过DFT后获得的复矩阵的模矩阵可以表示每个频率信号的强度(也可看作先做自相关后再进行傅里叶变换),经过适当处理即可转化为灰度能量谱图片。
线性噪声在频域中通常为点或线,因此可以通过傅里叶变换后进行滤波再通过逆变换复原图片。
算法实现
在实际实现时,根据欧拉公式, e − j → t = c o s t − j → sint , e j → t = c o s t + j → sint e^{- \overrightarrow{j}t} = cost - \overrightarrow{j}\text{sint},\ e^{\overrightarrow{j}t} = cost + \overrightarrow{j}\text{sint} e−jt=cost−jsint, ejt=cost+jsint,因此傅里叶变换的核矩阵可以表示为 W ik = cos ( 2 π i k ) − j → sin ( 2 π i k ) N \mathcal{W}_{\text{ik}} = \frac{\cos\left( 2\pi ik \right) - \overrightarrow{j}\sin\left( 2\pi ik \right)}{N} Wik=Ncos(2πik)−jsin(2πik),为方便运算将 W \mathcal{W} W分解为虚部系数 W lm \mathcal{W}_{\text{lm}} Wlm和实部系数 W re \mathcal{W}_{\text{re}} Wre,其中则 W = W re + j → W lm \mathcal{W} = \mathcal{W}_{\text{re}} + \overrightarrow{j}\mathcal{W}_{\text{lm}} W=Wre+jWlm。变换结果同样分解为 G = G re + j → G lm G = G_{\text{re}} + \overrightarrow{j}G_{\text{lm}} G=Gre+jGlm,则DFT可以表示为:
G = W ∗ g W = ( W re − j → W lm ) g ( W re + j → W lm ) = W re g W re + W lm g W lm − j → ( W lm g W re + W re g W lm ) G = \mathcal{W}^{*}g\mathcal{W =}\left( \mathcal{W}_{\text{re}} - \overrightarrow{j}\mathcal{W}_{\text{lm}} \right)g\left( \mathcal{W}_{\text{re}} + \overrightarrow{j}\mathcal{W}_{\text{lm}} \right) = \mathcal{W}_{\text{re}}g\mathcal{W}_{\text{re}} + \mathcal{W}_{\text{lm}}g\mathcal{W}_{\text{lm}} - \overrightarrow{j}\left( \mathcal{W}_{\text{lm}}g\mathcal{W}_{\text{re}} + \mathcal{W}_{\text{re}}g\mathcal{W}_{\text{lm}} \right) G=W∗gW=(Wre−jWlm)g(Wre+jWlm)=WregWre+WlmgWlm−j(WlmgWre+WregWlm)
{ G re = W re g W re + W lm g W lm G lm = − W lm g W re − W re g W lm \left\{ \begin{matrix} G_{\text{re}} = \mathcal{W}_{\text{re}}g\mathcal{W}_{\text{re}} + \mathcal{W}_{\text{lm}}g\mathcal{W}_{\text{lm}} \\ G_{\text{lm}} = - \mathcal{W}_{\text{lm}}g\mathcal{W}_{\text{re}} - \mathcal{W}_{\text{re}}g\mathcal{W}_{\text{lm}} \\ \end{matrix} \right.\ {Gre=WregWre+WlmgWlmGlm=−WlmgWre−WregWlm
同理,iDFT可以表示为:
g = ( W re + j → W lm ) ( G re + j → G lm ) ( W re − j → W lm ) g = \left( \mathcal{W}_{\text{re}} + \overrightarrow{j}\mathcal{W}_{\text{lm}} \right)(G_{\text{re}} + {\overrightarrow{j}G}_{\text{lm}})\left( \mathcal{W}_{\text{re}} - \overrightarrow{j}\mathcal{W}_{\text{lm}} \right) g=(Wre+jWlm)(Gre+jGlm)(Wre−jWlm)
其中,为了将能量谱转化为可见的灰度图,为能量谱取对数值进行归一化。且由于在频域中两个维度频率都为0时(即 W 00 \mathcal{W}_{00} W00处)为图像能量的总和,因此通过 l o g ( e + 1 ) ∗ 256 log ( W 00 + 1 ) log(e + 1)*\frac{256}{\log\left( \mathcal{W}_{00} + 1 \right)} log(e+1)∗log(W00+1)256可以做进一步归一化。