高斯混合模型（GMM）和EM算法

EM算法

EM算法是一种迭代算法，用于含有隐变量的概率模型参数的极大似然估计。每一次迭代由两步组成：E步，求期望（expectation）；M步，求极大（maximazation）。不断循环直到算法收敛，最后得出参数的估计。

之所以要搞得这么麻烦，就是因为有隐变量（latent variable）这个东西的存在，隐变量是无法观测的，这就造成了我们的观测值和想要预测的参数值之间的差距。如果所有的变量都是可观测的，我们使用极大似然法就可以得出对参数的估计了。

一般地，我们用Y表示观测随机变量的数据，Z表示隐随机变量的数据，Y和Z连在一起称为完全数据。假设给定观测数据Y，其概率分布是 P(Y|θ) ， θ 为要估计的参数，那么Y的对数似然函数为 L(θ)=logP(Y|θ) 。Y和Z的联合概率分布是 P(Y,Z|θ) ，它的对数似然函数为 logP(Y,Z|θ) 。

下面介绍EM算法的步骤：
输入：观测变量数据Y，隐变量数据Z， 联合分布 P(Y,Z|θ) ，条件分布 P(Z|Y,θ) （这里的两个分布应该指的是形式）
输出：模型参数

（1）选择参数的初始值 θ(0)
（2）E步： θ(i) 为第 i 步迭代的参数的估计值，在第 i+1 步，计算

Q(θ,θ(i))=EZ[logP(Y,Z|θ)|Y,θ(i)]=∑ZlogP(Y,Z|θ)P(Z|Y,θ(i))

（3）M步：求使得 Q(θ,θ(i)) 最大化的 θ ，作为第 i+1 次迭代的参数的估计值

θ(i+1)=argmaxθQ(θ,θ(i))

（4）重复第（2）（3）步，直到参数值收敛。

注意几个分布之间是有关系的，其实就是条件概率公式，只是多了个 θ

P(Y,Z|θ)=P(Y|θ)P(Z|Y,θ)=P(Z|θ)P(Y|Z,θ)

另外 EM算法对于初值的选取是敏感的，所以在实际中需要多选几个初始值多试几次。

上面的算法有些难以理解，因为我没有写推导过程，感兴趣的可以看看李航老师的《统计学习方法》P158“EM算法的导出”。总的来说就是我们本来要极大化的是观测数据的对数似然函数，即：

L(θ)=logP(Y|θ)=log∑ZP(Y,Z|θ)=log(∑ZP(Y|Z,θ)P(Z|θ))

这个似然函数对于简单的问题是可以处理的（可以参看《统计学习方法》9.1的三硬币模型作为参考），只是在EM算法中又进行了处理，它找出了似然函数的一个下界 B(θ,θ(i)) 即有 L(θ)≥B(θ,θ(i)) ，然后再M步中有

θ(i+1)=argmaxθB(θ,θ(i))=argmaxθQ(θ,θ(i))

所以EM算法我们不断求 θ 让Q函数值增加，从而让 B(θ,θ(i)) 不断增加，从而托着 L(θ) 不断增加，但是可以预料的是EM算法不能找到全局最优值，因为最后即使 θ 使得 B(θ,θ(i)) 达到了全局最优，但 B(θ,θ(i)) 只是 L(θ) 的下界，不能够保证 L(θ) 达到全局最优（也就是最大），所以在我看来，能够直接优化 L(θ) 的话就别这么麻烦了。

只看上面的算法不容易理解，下面介绍高斯混合模型，高斯混合模型的求解就利用了EM算法。

高斯混合模型（GMM）

高斯混合模型是采用概率模型来表达聚类原型的，他是假设整个数据集由k个高斯模型生成的，然后我们由EM算法求出模型参数以及每个数据点最有可能由哪个高斯模型生成，最后由同一个高斯模型生成的数据点划分成一类。
首先，下面是多元高斯分布的概率密度函数

p(x)=1(2π)n/2|Σ|2e−12(x−μ)TΣ−1(x−μ)

其中 μ 为均值向量。 Σ 为 n×n 的协方差矩阵，并且是对称的。这里的 μ,Σ 即为上面说过的模型参数 θ ，所以高斯分布的概率密度函数也记为 p(x|μ,Σ) 。

然后高斯混合分布可记为

pM(x)=∑i=1kαi⋅p(x|μi,Σi)

其中 αi 称为混合系数，满足条件 ∑ki=1αi=1 。
如果一个数据集由上面的模型生成，那么首先是按照 αi 挑选出相应的高斯模型，然后再从这个模型里面生成数据。回忆高斯模型的参数估计，我们用极大似然法就行了，但是在这里显然不行，因为我们不知道 αi 的取值，这里就用到了EM算法。所以下面讲一下高斯混合分布的过程。

令随机变量 zj∈{1,2,⋯,k} 表示样本 xj 属于哪一个高斯混合分布，其取值是不知道的，那么 zj 的先验概率 P(zj=j) （也就是随便一个样本是第 i 类的概率）其实就是 αi 。根据贝叶斯公式，有

pM(zj=i|xj)=P(zj=i)pM(xj|zj=i)pM(xj)=αi⋅p(xj|μi,Σi)∑kl=1αl⋅p(xj|μl,Σl)=γji

上式即为样本 xj 由第 i 个高斯分布生成的概率，相当于EM算法中的E步。显然这个值也是求不出来的，但是这个值可以用来估计其他参数。
这时我们再采用极大似然估计来估计模型参数，那么对数似然函数为

LL(D)=ln(∏j=1mpM(xj))=∑j=1mln(∑i=1kαi⋅p(xj|μi,Σi))

然后对这个对数似然函数相对参数 αi,μi,Σi 求导，令其为零，再求解，其实就是对这些参数进行更新，这就相当于是M步。注意这里涉及了向量和矩阵的求导，比较麻烦，我建议就是直接查公式，下面的结果来自《The Matrix Cookbook》

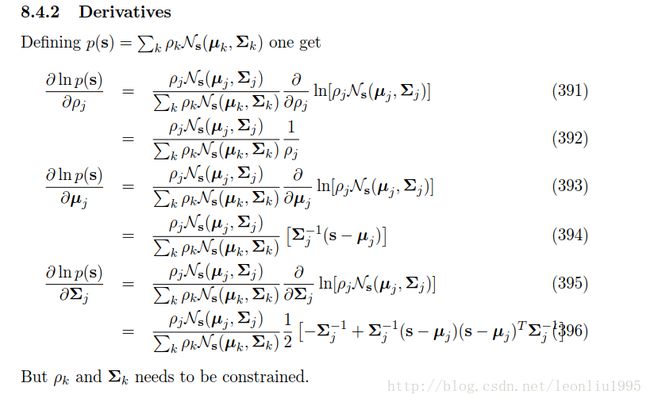
注意以上结果只是对于一个数据点而言的。
令 ∂LL(D)∂μi=0 ，在假设 γji 已知的情况下，可得

μi=∑mj=1γji⋅xj∑mj=1γji

同理令 ∂LL(D)∂Σi=0 可得

Σi=∑mj=1γji(xj−μi)(xj−μi)T∑mj=1γji

对于 αi 情况要复杂一些，因为有 ∑ii=1αi=1 的限制条件，所以利用拉格朗日乘子法，有拉格朗日函数：

LL(D)+λ(∑i=1kαi−1)

再对上式求 αi 的导数，并令其为0，可得

∑j=1mp(xj|μi,Σi)∑kl=1αl⋅p(xj|μl,Σl)+λ=0

对式子两边同时乘以 αi 并对所有的混合成分求和（就是所有的i），然和可以得到 λ=−m ，
那么再代回上式可得

αi=1m∑j=1mγji

经过以上几步计算，可以看到，我们在假设知道 γji 的情况下，又更新了 αi,μi,Σi ，而这几个参数又可以反过来更新参数 γji ，这是一个反复迭代的过程。可以证明这个过程是一定可以收敛的，但是不一定是最优值，所以要选择多个初始值进行多次计算。假设最后 γji 已经收敛了，那么每个样本的簇标记由下面的式子确定

λj=argmaxi∈{1,2,⋯,k}γji

即概率最大的标记。

回顾整个过程，我们的基本假设是数据集是由多个多维高斯分布的和组成，然后数据点就相当于是上面EM算法的推导中的输出 y ，混合系数 αi 是隐变量，因为是无法直接观测的。但是整个过程和上面所说的EM算法的流程还是有一点差别，首先我们优化的是输出 y 的对数似然函数，而不是上面算法中的Q函数，另外在E步中我们求的是后验概率，也不是期望。所以我认为EM算法的关键是这种在隐变量存在的情况下，通过一个中间变量不断迭代求出最后结果的思想

一个scikit-learn 中的简单例子

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from sklearn import mixture

n_samples = 300
np.random.seed(0)
shifted_gaussian = np.random.randn(n_samples, 2)+ np.array([20,20])
#这是个平移过的高斯分布
C = np.array([[0,-0.7],[3.5,.7]])
stretched_gaussian = np.dot(np.random.randn(n_samples, 2),C)
#这个高斯分布经过了伸缩，就是乘以矩阵C得来的，注意这里的np.dot函数，对于矩阵和向量
#就是普通的矩阵乘法和向量的点乘，但是对于这里的情况，结果是矩阵C分别右乘randn生成的(300,2)的矩阵的每一行，所以相当于是对生成的高斯分布的每个点都进行了伸缩。
X_train = np.vstack([shifted_gaussian, stretched_gaussian])
clf = mixture.GaussianMixture(n_components = 2, covariance_type = 'full')
#GMM的分类器，n_components 代表有几个高斯分量，covariance_type 代表协方差矩阵的类型，'full'代表每个高斯分量都有自己的协方差矩阵，另外比如还有'tied',代表每个分量的协方差矩阵都是相同的
clf.fit(X_train)
x = np.linspace(-20.0, 30.)
y = np.linspace(-20., 40.)
X, Y = np.meshgrid(x,y)
XX = np.array([X.ravel(), Y.ravel()]).T
Z=  -clf.score_samples(XX)
#score_samples ：Compute the weighted log probabilities for each sample
#我的理解就是一个样本属于某一分量的概率，也就是假如某个点被划分到某个分量，但它的这个值比较小，那么我们就可以猜测这个点很有可能不是属于这个类的
Z = Z.reshape(X.shape)

CS = plt.contour(X,Y,Z, norm = LogNorm(vmin = 1.0, vmax = 1000.0),  levels = np.logspace(0,3,10))
CB = plt.colorbar(CS, shrink = 0.8, extend = 'both')
plt.scatter(X_train[:,0], X_train[:,1], .8)

plt.title('Negative log-likelihood predicted by a GMM')
plt.axis('tight')
plt.show()

下面是结果

综上，本文大致讲了下高斯混合模型和EM算法，但我觉得二者都是思想更重要，两种方法的应用都不止在这里，比如高斯混合模型我知道在视频的运动前景提取中就有利用它来提取前景的。