Tarjan算法_LCA

首先我们要知道什么是LCA、深度优先生成树以及并查集

在计算LCA的算法中我们有离线算法以及在线算法两种，我们这里使用的Tarjan算法是使用的是离线算法，即将所有的问题一次性输入，然后再一次性输出答案

本人感觉这个算法的写法和Tarjan写法还是有很大差距的，相同的地方大部分是在思想上

我们首先来举个例子，模拟一下这个算法的实现过程

假设这是我们要计算的树，我们要计算7--8，5--6，5--2，4--6，它们四个的LCA。首先我们要从根节点1向下遍历，首先遍历到2，然后遍历2的叶子节点，继续遍历到节点7，我们发现节点7没有叶子节点了，那么我们就把vis[7] = true，然后我们要在问题中寻找是否有和7相关的，我们发现7-8中包含7，但是vis[8] = false，所以先不管，接着向上回溯,然后我们就将per[7] = 4，per数组就是并查集中不断向上传递的数组。到达4，我们发现4的所有叶子节点也已经全部遍历完了，然后更新vis[4] = true,然后再从问题中找含有4的问题，发现4--6包含4，但是vis[6] = false,所以什么都不能做，继续回溯到节点2,节点4已经完成了，更新per[4] =2；

我们据需从节点2遍历，然后进入节点5，之后进入节点8，但是在节点8处,vis[8] = true;我们在找包含8的问题，我们发现7--8，这是vis[7]=true,所以这是这个问题的答案就是Find(7)，Find函数表示并查集中寻找最终父亲节点的函数，这是Find(7) = 2，所以7和8的LCA = 2；继续回溯到5，然后接着更新per[8] = 5,vis[5] = true;和上面类似，没有问题可以求解回溯更新per[5] = 2。

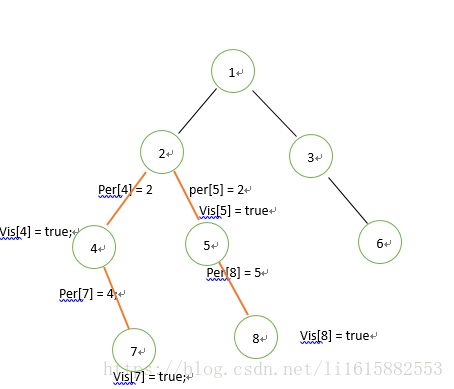
走到2时，2已经没有叶子节点没有遍历了，所以vis[2] = true;然后再问题中找寻和2相关的问题，发现2--5中包含，并且vis[5] = true，所以2和5的LCA就是Find(5) = 2，然后接着回溯，更新per[2] = 1；

剩余的就不再接着向下说了，步骤都是类似的，并且程序写起来十分容易懂。

//不怕别人比你聪明，就怕别人比你聪明还比你努力
#include
#include
#include
#include
#include
#include
#include 
#include 
#include 

在计算LCA的算法中Tarjan离线算法还是比较简单的，后面我会写一下他的在线算法.....

参考博客

深度优先生成树：https://www.cnblogs.com/llhthinker/p/4954082.html

并查集：https://segmentfault.com/a/1190000004023326