AVL树，红黑树，B树与B+树

总体对比：
https://blog.csdn.net/whoamiyang/article/details/51926985

AVL树

https://www.cnblogs.com/skywang12345/p/3576969.html

最先发明的自平衡二叉查找树，也被称为高度平衡树。相比于”二叉查找树”，它的特点是：AVL树中任何节点的两个子树的高度最大差别为1。
AVL树的查找、插入和删除在平均和最坏情况下都是O(logn)。

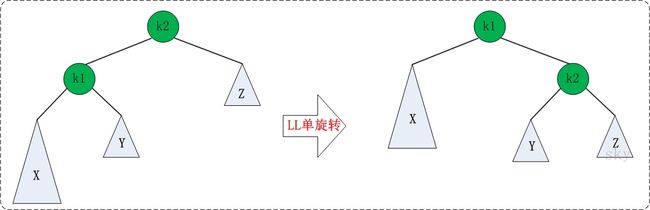
在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)和RL(右左)。下面给出它们的示意图：

LL：左子树的左子树导致的失衡，其余依次类推。

LL的旋转：

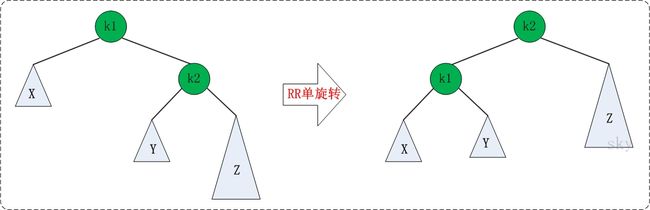
RR的旋转

LR的旋转

RL的旋转

总结：发生问题的那个节点要成为根节点才能解决问题。不管我们是执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而旋转是非常耗时的,由此我们可以知道AVL树适合用于插入删除次数比较少，但查找多的情况。

红黑树

https://www.cnblogs.com/skywang12345/p/3245399.html

红黑树只追求近似平衡，所以在插入与删除节点时，翻转次数远远少于平衡树，因此在需要较多插入删除操作的场景中，使用红黑树更好。同样也因为近似平衡，所以在查询时，红黑树查询的深度可能会大于平衡二叉树，所以在需要较多查询的场景中，使用平衡二叉树更好。

红黑树近似平衡：深度最大的节点的深度<= 2 * 深度最小的节点的深度。

先说这个颜色，晚上一大票博文都是上来就给你五条性质，为什么要红色黑色也不说下，根本看不懂！！！

为什么要有颜色，因为要满足近似平衡。

再来看五条性质：

性质1 . 节点是红色或黑色。

性质2 . 根节点是黑色。

性质3 . 每个叶节点（NIL节点，空节点）是黑色的。

性质4 . 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

性质5 . 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

因为性质5，所以延伸除了近似平衡状态，试想根节点到每个叶子节点的黑色节点个数相同，而每两个红色节点之间不能直接相连，根节点又必须为黑色，红节点数小于黑节点数，所以推导出：黑色节点个数<=每条路径的总节点个数<=2倍的黑色节点数，所以最大深度与最小深度的最多相差一倍。

因为性质5，默认新插入的节点都为红色，就算有颜色冲突，也可以通过变色和旋转来修改树。

注意：红黑树的查找、删除、添加操作都为log(n)。

插入操作：

1.将插入的节点着色为”红色”。已满足性质5

2.参考上面的性质，只可能不满足性质4

3.根据被插入节点的父节点的情况，划分为三种情况来处理。

① 情况说明：被插入的节点是根节点。
处理方法：直接把此节点涂为黑色。
② 情况说明：被插入的节点的父节点是黑色。
处理方法：什么也不需要做。节点被插入后，仍然是红黑树。
③ 情况说明：被插入的节点的父节点是红色。
处理方法：那么，该情况与红黑树的“特性(4)”相冲突。这种情况下，被插入节点是一定存在非空祖父节点的；进一步的讲，被插入节点也一定存在叔叔节点(当前节点的祖父节点的另一个子节点，空节点也算)。理解这点之后，我们依据”叔叔节点的情况”，将这种情况进一步划分为3种情况(Case)。

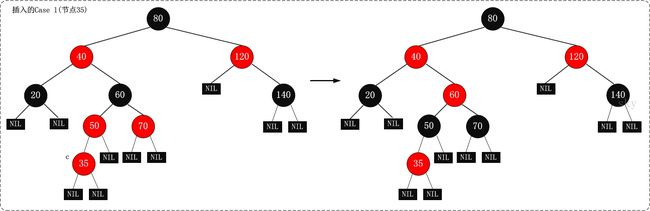
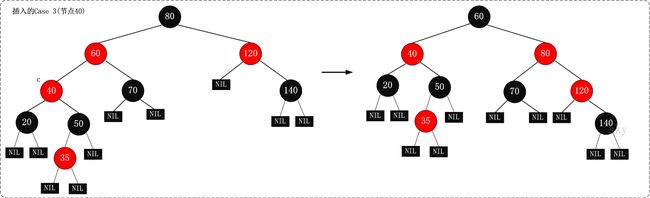
Case1 ：

就是变色，把祖父节点变为红色，父节点叔叔节点变为黑色，这样在这几个节点中不会不满足性质。若此时，祖父节点是根节点，直接将祖父节点设为“黑色”，那就完全解决这个问题了；若祖父节点不是根节点，那我们需要将“祖父节点”设为“新的当前节点”，接着对“新的当前节点”进行分析。

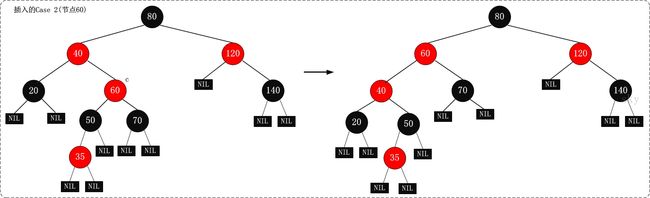
Case2：

继续把40作为当前节点，因为问题要从下层开始解决。

case3：

把120当作当前节点

删除，略过，直接看原文吧，这只是简单介绍。

B树，B+树

https://blog.csdn.net/guoziqing506/article/details/64122287

B树是一种查找树，我们知道，这一类树（比如二叉查找树，红黑树等等）最初生成的目的都是为了解决某种系统中，查找效率低的问题。B树也是如此，它最初启发于二叉查找树，二叉查找树的特点是每个非叶节点都只有两个孩子节点。然而这种做法会导致当数据量非常大时，二叉查找树的深度过深，搜索算法自根节点向下搜索时，需要访问的节点也就变的相当多。如果这些节点存储在外存储器中，每访问一个节点，相当于就是进行了一次I/O操作（因为每一层的节点都在一个磁盘上），随着树高度的增加，频繁的I/O操作一定会降低查询的效率。所以B树就被搞出来降低树的高度，从而减少磁盘的访问。

1. B树的定义

最小度数为t的B树满足：

一个标准的B树如下图：

1. B树的高度

最小度数t，包含n个关键字的B树的高度：

在搜索B树时，很明显，访问节点（即读取磁盘）的次数与树的高度呈正比，而B树与红黑树和普通的二叉查找树相比，虽然高度都是对数数量级，但是显然B树中log函数的底可以比2更大，因此，和二叉树相比，极大地减少了磁盘读取的次数。

B+树看原文