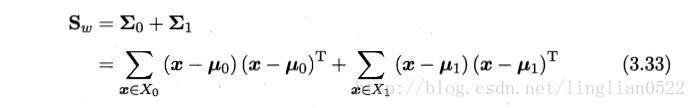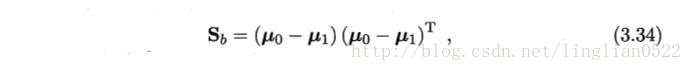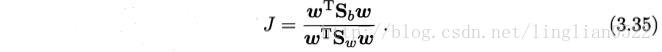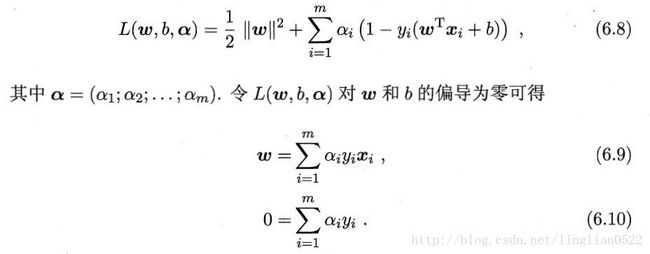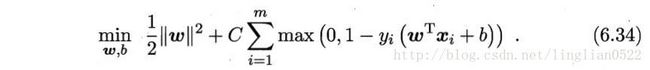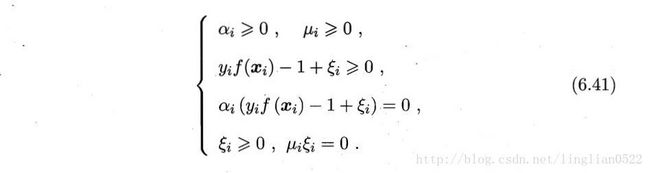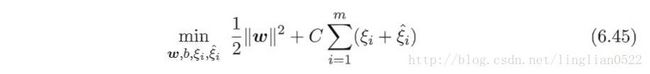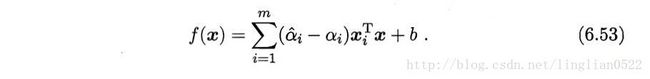机器学习-学习笔记 学习总结归纳（第六周）
对数几率回归
考虑分类问题时使用对数几率回归。
在二分类问题中，其输出标记y(0, 1)， 而在线性回归中，输出标记y是实值，所以我们需要将问题转为单位阶跃函数
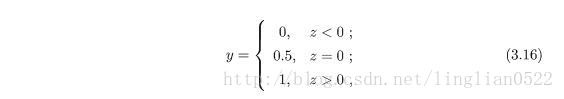
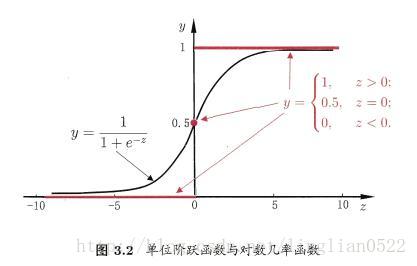
但是可以看出，单位阶不连续，所以我们可以将函数转换为对数几率函数。
转化为
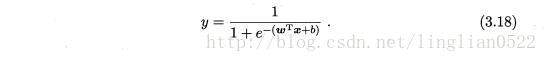
也可转换为
如何确定上述式子中的w和b
我们可以通过使用极大似然法来估计w和b，经典算法有梯度下降法和牛顿法。
线性判别分析
LDA的思想
先给定一个数据集
具体定义如下
当满足思想的时候，可以得到下面这个式子。
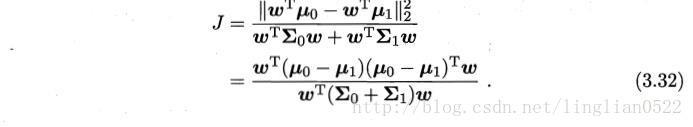
类内散度矩阵
类间散度矩阵
最后可以得到如下式子，即我们所要求的式子
多分类学习
基本思路为“拆解法”（多分类拆解为多个二分类来进行求解）。
分为三种
1. 一对一
2. 一对其余
3. 多对多
ECOC
解码和编码
类别最后通过“编码矩阵”来指定。
纠错输出码
神经网络
学习是神经网络一种最重要也最令人注目的特点。在神经网络的发展进程中,学习算法的研究有着十分重要的地位。目前,人们所提出的神经网络模型都是和学习算法相应的。所以,有时人们并不去祈求对模型和算法进行严格的定义或区分。有的模型可以有多种算法。而有的算法可能可用于多种模型。在神经网络中,对外部环境提供的模式样本进行学习训练,并能存储这种模式,则称为感知器;对外部环境有适应能力,能自动提取外部环境变化特征,则称为认知器。神经网络在学习中,一般分为有教师和无教师学习两种。感知器采用有教师信号进行学习,而认知器则采用无教师信号学习的。在主要神经网络如Bp网络,Hopfield网络,ART络和Kohonen网络中;Bp网络和Hopfield网络是需要教师信号才能进行学习的;而ART网络和Khonone网络则无需教师信号就可以学习。所谓教师信号,就是在神经网络学习中由外部提供的模式样本信号。
神经元模型
神经网络的基本组成单元是神经元，在数学上的神经元模型是和在生物学上的神经细胞对应的。或者说，人工神经网络理论是用神经元这种抽象的数学模型来描述客观世界的生物细胞的。
很明显，生物的神经细胞是神经网络理论诞生和形成的物质基础和源泉。这样，神经元的数学描述就必须以生物神经细胞的客观行为特性为依据。因此，了解生物神经细胞的行为特性就是一件十分重要而必须的事了。
神经网络的拓朴结构也是以生物学解剖中神经细胞互连的方式为依据的。对神经细胞相互作用情况的揭露也是十分重要的。
神经元是神经网络基本元素。只有了解神经元才能认识神经网络的本质。在这一节介绍神经元的生物学解剖，信息的处理与传递方式，工作功能以及其数学模型。
M-P神经元模型
这里引入M-P神经元模型。
我们可以概括出生物神经网络的假定特点：
1. 每个神经元都是一个多输入单输出的信息处理单元；
2. 神经元输入分兴奋性输入和抑制性输入两种类型；
3. 神经元具有空间整合特性和阈值特性；
4. 神经元输入与输出间有固定的时滞，主要取决于突触延搁
而M-P模型的6个特点：
1. 每个神经元都是一个多输入单输出的信息处理单元；
2. 神经元输入分兴奋性输入和抑制性输入两种类型；
3. 神经元具有空间整合特性和阈值特性；
4. 神经元输入与输出间有固定的时滞，主要取决于突触延搁；
5. 忽略时间整合作用和不应期；
6. 神经元本身是非时变的，即其突触时延和突触强度均为常数。
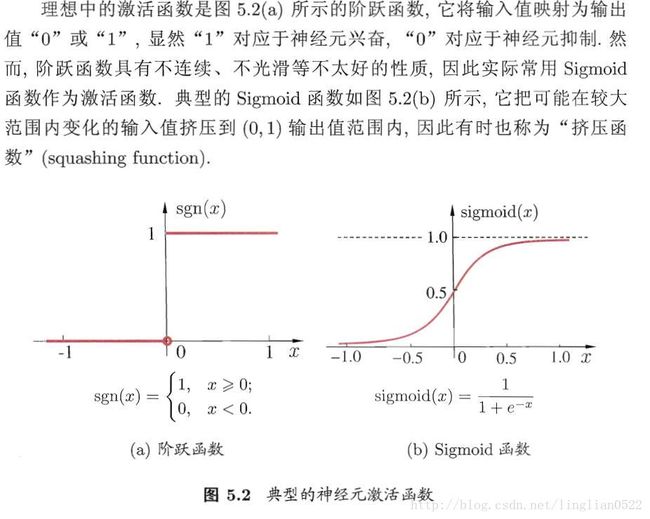
这里主要注意一下激活函数的概念即可。
详情请见M-P神经元模型
感知机与多层网络
感知机
感知机由二层神经元组成.
感知机只有输出层神经元进行激活函数的处理，只能解决线性问题。
如果需要解决线性问题，则考虑使用多层功能神经元.
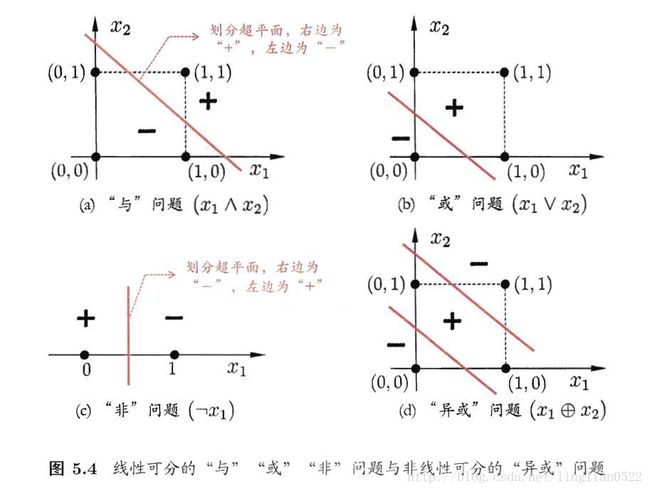
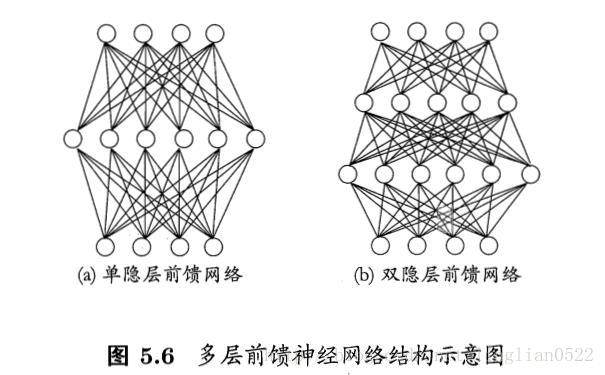
多层网络
多叉树- -
分为输入层神经元和输出层神经元
这个模型很经典，训练的话，就是训练这个模型，删除多余的链接，还记得第一章的那个西瓜嘛- -
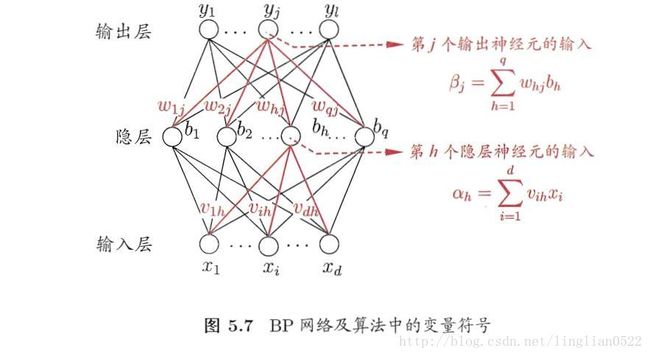
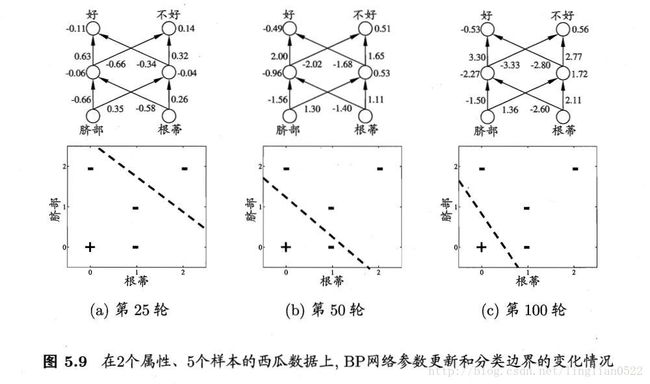
误差逆传播算法
在单层网络模型中，我们只需要简单的考虑线性模型即可， 但是在多层网络模型中，那简单的线性模型就完全不够了（配合感知机学习规则），我们需要用到误差逆传播算法（BP）。
BP
这里也称为反向传播算法。
BP算法(即反向传播算法)是在有导师指导下，适合于多层神经元网络的一种学习算法，它建立在梯度下降法的基础上。BP网络的输入输出关系实质上是一种映射关系：一个n输入m输出的BP神经网络所完成的功能是从n维欧氏空间向m维欧氏空间中一有限域的连续映射，这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合，因此具有很强的函数复现能力。这是BP算法得以应用的基础。
BP工作流程
更新连接权和阈值示意图
全局最小与局部极小
注意，理解局部极小和全局最小的概念！
当遇到有多个局部极小的情况
其他神经网络
- RBF(径向基网络)
竞争性学习
* ART(自适应谐振理论)
SOM(自组织映射)
级联相关网络
Elman网络
Boltzman机（基于能量的模型）
分为受限和不受限
卷积神经网络
- 每个卷积层包含多个特征映射，每个特征映射是一个由多个神经元构成的“平面”，通过一种卷积滤波器提取输入的一种特征
- 采样层亦称“汇合层”，其作用是基于局部相关性原理进行亚采样，从而在减少数据量的同事保留有用信息
- 连接层就是传统神经网络对隐层与输出层的全连接
支持向量机
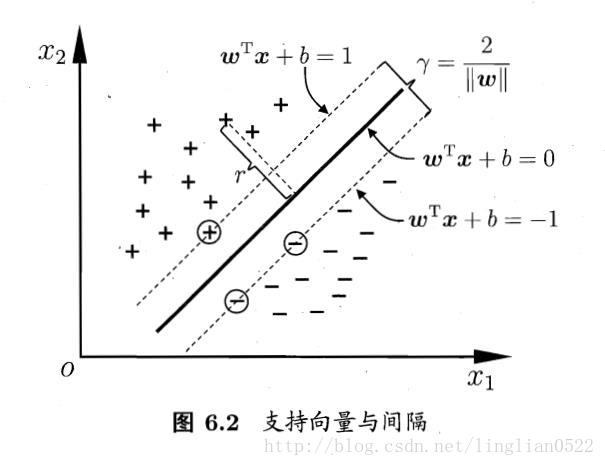
间隔与支持向量
划分超平面可通过如下线性方程来描述:
下图中的等式称为支持向量，二个等式之间的距离称为间隔。
目的就是找到最大间隔的划分超平面。
对偶问题
由上述式子可以得到对偶问题
最终得到如下公式
满足条件
核函数
异或问题就不是线性可分的。
核函数，支持向量展式
核函数定理
支持向量机 通过某非线性变换 φ( x) ，将输入空间映射到高维特征空间。特征空间的维数可能非常高。如果支持向量机的求解只用到内积运算，而在低维输入空间又存在某个函数 K(x, x′) ，它恰好等于在高维空间中这个内积，即K( x, x′) =<φ( x) ⋅φ( x′) > 。那么支持向量机就不用计算复杂的非线性变换，而由这个函数 K(x, x′) 直接得到非线性变换的内积，使大大简化了计算。这样的函数 K(x, x′) 称为核函数。
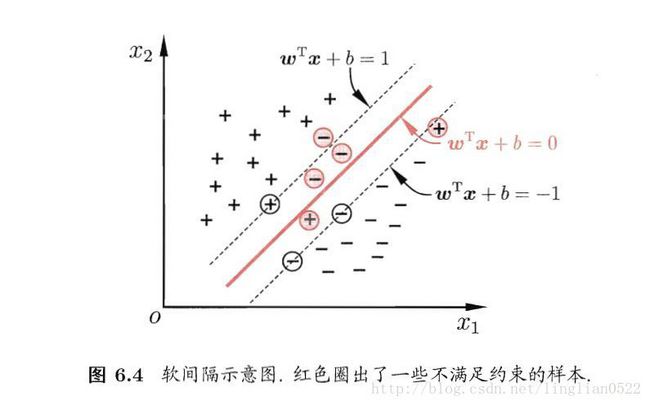
软间隔与正则化
为了缓解过拟合问题，引入软间隔的概念。
前面介绍的间隔为硬间隔，即所有样本都必须划分正确，而软间隔则允许有特例。
在最大化间隔的同时，不满足约束的样本应该尽可能的少，所以，优化目标可写成
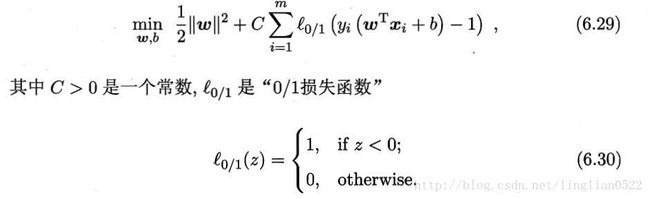
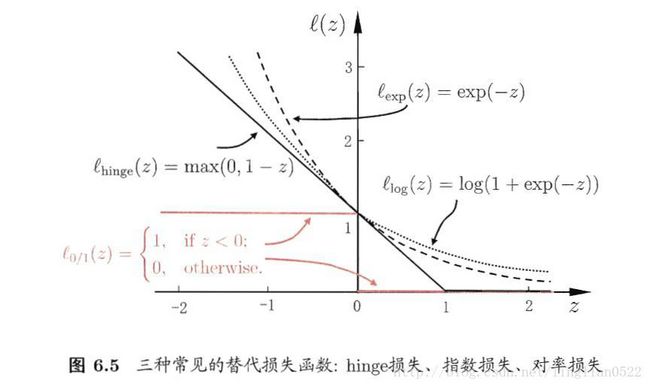
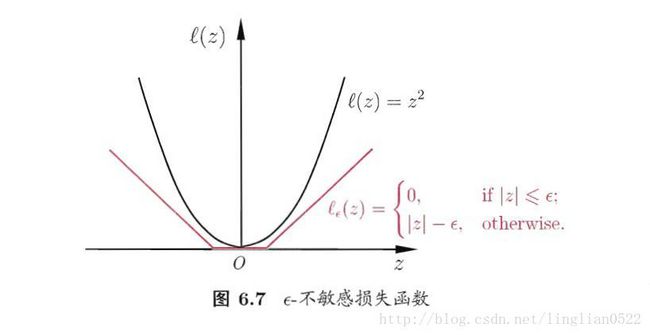
人们通常使用一些其他函数来代替上述中的l，称为替代损失。
通常有以下三种
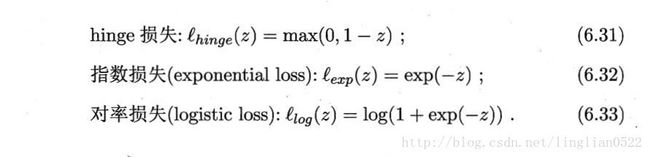
软间隔支持向量机（hinge损失）
接着引入松弛变量
得到的对偶问题
KKT条件
得出，软间隔支持向量机的最终模型仅与支持向量有关，即hinge损失函数仍然保持了稀疏性。
正则化
概念
支持向量回归(SVR)
就是通过一定的差值判断，而不是以前的必须完全相同才算正确的样例。
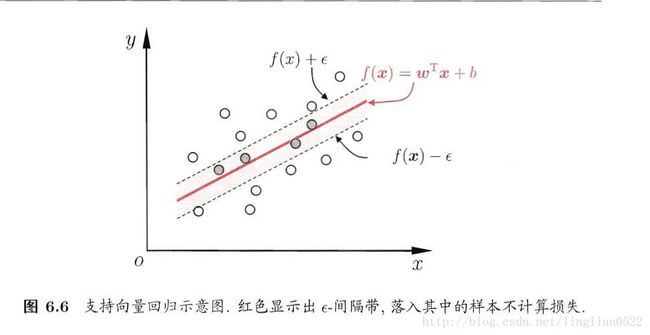
问题形式化：
其中的不敏感损失函数
引入松弛变量
最后可得
若考虑特征映射形式
核方法
定理
何为核方法
