Andrew Ng-深度学习-第二门课-week1(正则化和权重初始化)
文章目录
- 1.训练,验证,测试集
- 2 偏差,方差(Bias /Variance)
- 3 机器学习基础
- 4 正则化
- 4.1 L2正则化:
- 4.1.1 基础知识:
- 4.1.2为什么L2正则化可以防止模型过拟合:
- 4.2 L1正则化:
- 4.2.1 基础知识:
- 4.2.2 为什么L1正则化可以产生稀疏模型:
- 4.2.3 L1正则化如何求导:
- 6 dropout 正则化:
- 如何实现dropout:inverted dropout
- 实施技巧:
- 8.其他正则化方法
- 1.数据扩增:
- 2.early stopping:
- 9 归一化输入
- 为什么进行归一化:
- 11.神经网络的权重初始化
第二门课,改善深层神经网络:超参数调试、正则化以及优化。第一周课程,深度学习的实践层面。
1.训练,验证,测试集
数据划分:
- 以前,70%验证集,30%测试集或者60%训练,20%验证和20%测试集来;
- 大数据时代:训练集占98%,验证集和测试集各占1%即可
尽可能保证数据集匹配,即训练集、测试集、验证集合分布一致。
2 偏差,方差(Bias /Variance)
- 偏差:欠拟合
- 方差:过拟合
3 机器学习基础
解决方差偏差问题的基本方法:
- 1.训练模型,确定偏差高不高,如果偏差较高,试着评估训练集或训练数据的性能:
更多隐藏层或者隐藏单元的网络,花更多时间训练网络,尝试更先进的优化算法 - 2.偏差降低到可以接受的数值,检查方差有没有问题:采用更多数据(最好)、正则化
注意点:
- 明确存在的问题是偏差还是方差,哪个问题更严重;
- 偏差方差权衡问题,构建复杂网络可以在不影响方差的同时减少偏差,采用更多数据可以在不过多影响偏差的同时减少方差
4 正则化
4.1 L2正则化:
4.1.1 基础知识:
定义: L2正则化是指权值向量 w w w中各个元素的平方和, ∑ j = 1 n x w 2 \sum_{j= 1}^{n_{x}}{w^2} ∑j=1nxw2 (二范数)
Ridge回归(岭回归): 在线性回归模型中使用L2正则化
神经网络的正则项: 对每一层参数的二范数进行求和
λ 2 m ∑ 1 L ∣ ∣ W [ l ] ∣ ∣ 2 \frac{\lambda }{2m}{{\sum\nolimits_{1}^{L}{||{{W}^{[l]}}||}}^{2}} 2mλ∑1L∣∣W[l]∣∣2
- L L L是神经网络所含的层数
- m m m:训练样本数
- ∣ ∣ W [ l ] ∣ ∣ 2 {||W^{\left[l\right]}||}^{2} ∣∣W[l]∣∣2(矩阵二范数):矩阵中所有元素的平方求和;
作用:
- 防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
4.1.2为什么L2正则化可以防止模型过拟合:
-
直观理解:
就是 λ \lambda λ增加到足够大, W W W会接近于0,消除或至少减少许多隐藏单元的影响,最终这个网络会变得更简单。 -
梯度下降角度:
假设我们的损失函数是:
J = J 0 + λ 2 m ∑ W [ l ] 2 J = J_0 + \frac{ \lambda }{2m}{{\sum{{{W}^{[l]}}}}^{2} } J=J0+2mλ∑W[l]2
利用梯度下降对参数进行更新:
θ j : = θ j ( 1 − α λ m ) − ∂ ∂ θ j J ( θ ) \theta_{j} :=\theta_{j}\left(1-\alpha \frac{\lambda}{m}\right) - \frac{\partial}{\partial \theta_{j}} J(\theta) θj:=θj(1−αmλ)−∂θj∂J(θ)
如果没有 L 2 L2 L2正则化,参数更新公式是:
θ j : = θ j − ∂ ∂ θ j J ( θ ) \theta_{j} :=\theta_{j} - \frac{\partial}{\partial \theta_{j}} J(\theta) θj:=θj−∂θj∂J(θ)
从两个公式中我们可以明显看出,参数 θ j \theta_{j} θj多减了一部分 θ j α λ m \theta_{j}\alpha \frac{\lambda}{m} θjαmλ,这会使得参数变得更小。 -
激活函数角度理解:
假设我们的激活函数 g ( z ) = t a n h ( z ) , z = W a + b g(z) = tanh(z),z = Wa + b g(z)=tanh(z),z=Wa+b, W ↓ → z ↓ W↓ → z↓ W↓→z↓当 z z z很小的时候,激活函数会处于线性区,在线性区,不过NN如何叠加,模型最终都是接近于一个线性函数,所以可以有效防止过拟合。
4.2 L1正则化:
4.2.1 基础知识:
定义: L1正则化是指权值向量w ww中各个元素的绝对值之和, ∑ j = 1 n x ∣ w ∣ \sum_{j= 1}^{n_{x}}{|w|} ∑j=1nx∣w∣ (一范数)
Lasso回归: 线性回归模型,使用L1正则化
作用:
- L产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
4.2.2 为什么L1正则化可以产生稀疏模型:
假设有如下带L1正则化的损失函数:
J = J 0 + α ∑ w ∣ w ∣ J=J_{0}+\alpha \sum_{w}|w| J=J0+αw∑∣w∣
其中 J 0 J_0 J0是原始的损失函数,加号后面的一项是 L 1 L1 L1正则化项, α \alpha α是正则化系数。我们需要通过梯度下求损失函数的最小值, L 1 L1 L1正则化是权值的绝对值之和, J J J是带有绝对值符号的函数,因此 J J J是不完全可微的。在原始损失函数 J 0 J_0 J0后添加L1正则化项,相当于对 J 0 J_0 J0 做了一个约束。令 L = α ∑ w ∣ w ∣ L = \alpha \sum_w{|w|} L=α∑w∣w∣,则 J = J 0 + L J = J_0 + L J=J0+L,任务变成在 L L L约束下求 J 0 J_0 J0最小值的解。
考虑二维的情况,即只有两个权值 w 1 , w 2 w^1,w^2 w1,w2,此时 L = ∣ w 1 ∣ + ∣ w 2 ∣ L=|w1|+|w2| L=∣w1∣+∣w2∣,利用梯度下降法,求解 J 0 J_0 J0。可以画出 J 0 J_0 J0等值线,以及正则项 L 1 L_1 L1,在二维平面上画出来。如下图:
图中等值线是 J 0 J_0 J0 的等值线,黑色方形是 L L L函数的图形。在图中,当 J 0 J_0 J0 等值线与 L L L图形首次相交的地方就是最优解。上图中 J 0 J_0 J0与 L L L的一个顶点相交,这个顶点就是最优解。注意到这个顶点的值是 ( w 1 , w 2 ) = ( 0 , w ) (w1,w2)=(0,w) (w1,w2)=(0,w)。可以直观想象,因为 L L L函数有很多『突出的角』(二维情况下四个,多维情况下更多), J 0 J_0 J0与这些角接触的机率会远大于与L LL其它部位接触的机率,而在这些角上,会有很多权值等于0,这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
而正则化前面的系数 α \alpha α,可以控制 L L L 图形的大小。 α \alpha α越小, L L L的图形越大(上图中的黑色方框); α \alpha α越大, L L L的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值 ( w 1 , w 2 ) = ( 0 , w ) (w1,w2)=(0,w) (w1,w2)=(0,w)中的 w w w可以取到很小的值。
类似,假设有如下带L2正则化的损失函数: J = J 0 + α ∑ w w 2 J = J_0 + \alpha\sum_w{w^2} J=J0+α∑ww2
二维平面下L2正则化的函数图形是个圆,与方形相比,被磨去了棱角。因此 J 0 J_0 J0与 L L L相交时使得 w 1 , w 2 w1,w2 w1,w2等于零的机率小了许多,这就是为什么L2正则化不具有稀疏性的原因。
4.2.3 L1正则化如何求导:
采用近端梯度下降(坐标轴下降法),由泰勒公式展开,做一次替换,然后得到参数迭代公式。
对于目标函数中包含加性的非平滑项并使用梯度下降求解的问题,如果可以使用proximal operator,则解法如下:
假设目标函数为 min x f ( x ) + h ( x ) \min_x f(x) + h(x) minxf(x)+h(x) 其中 f ( x ) f(x) f(x)可导,而 h ( x ) h(x) h(x)不可导。
则每步迭代更新为 x k + 1 = P r o x h , η ( x k − η ▽ f ( x k ) ) x^{k+1} = Prox_{h,\eta}(x^k - \eta\triangledown f(x^k)) xk+1=Proxh,η(xk−η▽f(xk))
其中, P r o x h , η ( x ) = arg min y 1 2 η ∥ y − x ∥ 2 + h ( y ) Prox_{h,\eta} (x) = \arg\!\min_y \frac{1}{2\eta}\|y - x\|^2 + h(y) Proxh,η(x)=argminy2η1∥y−x∥2+h(y)
如果 h ( x ) = ∥ x ∥ 1 h(x) = \|x\|_1 h(x)=∥x∥1,也就是题目中要求的L1范数正则化,则对应的
P r o x h , η ( x ) = arg min y 1 2 η ∥ y − x ∥ 2 + ∥ y ∥ 1 = y ^ Prox_{h,\eta} (x) = \arg\!\min_y \frac{1}{2\eta}\|y - x\|^2 + \|y\|_1 = \hat{y} Proxh,η(x)=argminy2η1∥y−x∥2+∥y∥1=y^
y ^ i = { x i − η if x i − η > 0 x i + η if x i + η < 0 0 otherwise \hat{y}_i = \begin{cases} x_i - \eta & \text{if}\ x_i-\eta > 0 \\ x_i + \eta & \text{if}\ x_i+\eta < 0 \\ 0 & \text{otherwise} \\ \end{cases} y^i=⎩⎪⎨⎪⎧xi−ηxi+η0if xi−η>0if xi+η<0otherwise
参考自下列文章。
L1范数的最优化过程是怎么样的?梯度下降遇到不可导点怎么办?
6 dropout 正则化:
定义: 复制神经网络,dropout遍历网络的每一层的每个节点,以某个概率保留或消除这些节点,同时删除掉从该节点进出的连线,得到一个节点更少,规模更小的网络,然后用backprop方法进行训练。
如何实现dropout:inverted dropout
inverted dropout(反向dropout)这是最常用的一种方法。
-
1.假设神经网络有三层,对第三层实施dropout。
-
2.定义向量 d d d代表dropout向量, d [ 3 ] d^{[3]} d[3]表示网络第三层的dropout向量:
d3 = np.random.rand(a3.shape[0],a3.shape[1]) < keep_prob
k e e p _ p r o b keep\_prob keep_prob:表示保留某个隐藏单元的概率,0.8意味着消除任意一个隐藏单元的概率是0.2。它的作用就是生成随机矩阵,对应值为1的概率是0.8,对应为0的概率是0.2。 -
3.计算第三层的输出: a [ 3 ] a^{[3]} a[3],
a3 =np.multiply(a3,d3),这里是元素相乘,也可写为 a 3 ∗ = d 3 a3*=d3 a3∗=d3,乘法运算把 d [ 3 ] d^{\left\lbrack3 \right]} d[3]中相应元素输出,即让 d [ 3 ] d^{[3]} d[3]中0元素与 a [ 3 ] a^{[3]} a[3]中相对元素归零; -
4. a 3 = a 3 k e e p _ p r o b a_3 = \frac{a_3}{keep\_prob} a3=keep_proba3:为了确保 a [ 3 ] a^{[3]} a[3]期望值不变,如果不进行这一步骤,平均值会变得越来越复杂。
-
5.测试阶段不使用dropout:因为在测试阶段进行预测时,我们不期望输出结果是随机的,如果测试阶段应用dropout函数,预测会受到干扰。
实施技巧:
- dropout是一种正则化方法,它有助于预防过拟合,因此除非算法过拟合,不然我是不会使用dropout的;
- dropout一大缺点就是代价函数不再被明确定义,每次迭代,都会随机移除一些节点,如果再三检查梯度下降的性能,实际上是很难进行复查的
8.其他正则化方法
1.数据扩增:
尤其适用于图片和文本,对图片进行旋转,裁剪等。对文本进行句子顺序打乱等操作。
2.early stopping:
在训练过程中,参数会随着损失函数的下降变得非常大,在中间点停止迭代过程,可以使参数变得不会太大,起到防止过拟合的作用。
缺点:
不能独立处理欠拟合和过拟合这两个任务,提早停止梯度下降也就意味着不再尝试降低代价函数,模型的拟合能力就得不到保证。
优点:
只运行一次梯度下降,可以找出的较小值,中间值和较大值,而无需尝试正则化超级参数的很多值。
L2正则化会使得超级参数搜索空间更容易分解,也更容易搜索,但是缺点在于,你必须尝试很多正则化参数的值,这也导致搜索大量值的计算代价太高。
9 归一化输入
归一化的两个步骤: x − μ σ 2 \frac{x-\mu}{\sigma^2} σ2x−μ
- 零均值化: μ = 1 m ∑ i = 1 m x ( i ) \mu = \frac{1}{m}\sum_{i =1}^{m}x^{(i)} μ=m1∑i=1mx(i)
- 归一化方差: σ 2 = 1 m ∑ i = 1 m ( x ( i ) ) 2 \sigma^{2}= \frac{1}{m}\sum_{i =1}^{m}{({x^{(i)})}^{2}} σ2=m1∑i=1m(x(i))2
为什么进行归一化:
回想代价函数 J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b)=\frac{1}{m}\sum\limits_{i=1}^{m}{L({{{\hat{y}}}^{(i)}},{{y}^{(i)}})} J(w,b)=m1i=1∑mL(y^(i),y(i)),对于未进行归一化的数据,代价函数会像个狭长的碗,梯度下降法可能需要多次迭代过程,直到最后找到最小值。归一化后,代价函数优化起来更简单快速。
11.神经网络的权重初始化
为了解决梯度消失和梯度爆炸的问题,一定程度上可以通过选择权重初始化来解决。考虑单个神经元的例子。
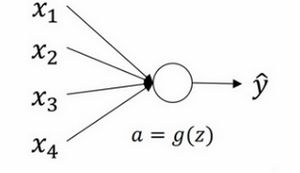
z = w 1 x 1 + w 2 x 2 + … + w n x n z = w_{1}x_{1} + w_{2}x_{2} + \ldots +w_{n}x_{n} z=w1x1+w2x2+…+wnxn, b = 0 b=0 b=0,为了预防 z z z值过大或过小, n n n越大,希望 w i w_{i} wi越小,因为 z z z是 w i x i w_{i}x_{i} wixi的和,如果你把很多此类项相加,希望每项值更小,最合理的方法就是设置 w i = 1 n w_{i}=\frac{1}{n} wi=n1, n n n表示神经元的输入特征数量。
为了保证方差不变,对每层的权重矩阵增加一个系数(Xavier初始化):
- Tanh: w [ l ] = n p . r a n d o m . r a n d n ( shape ) ∗ np.sqrt ( 1 n [ l − 1 ] ) w^{[l]} = np.random.randn( \text{shape})*\text{np.}\text{sqrt}(\frac{1}{n^{[l-1]}}) w[l]=np.random.randn(shape)∗np.sqrt(n[l−1]1), n [ l − 1 ] n^{[l - 1]} n[l−1]是第 l − 1 l-1 l−1层神经元数量);
- Relu: w [ l ] = n p . r a n d o m . r a n d n ( shape ) ∗ np.sqrt ( 2 n [ l − 1 ] ) w^{[l]} = np.random.randn( \text{shape})*\text{np.}\text{sqrt}(\frac{2}{n^{[l-1]}}) w[l]=np.random.randn(shape)∗np.sqrt(n[l−1]2), n [ l − 1 ] n^{[l - 1]} n[l−1]是第 l − 1 l-1 l−1层神经元数量);
权重初始化为上一层神经元数量的函数。

