Andrew Ng-深度学习-第二门课-week2(优化算法)
从GD出发梳理优化算法的演变和各个优化算法的优缺点。
1.梯度下降:
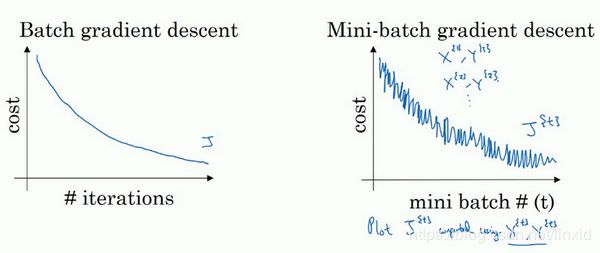
1.1 批量梯度下降(batch gradient descent)
每次迭代更新参数,在整个数据集上计算所有的梯度。
θ = θ − η ⋅ ∇ θ J ( θ ) \theta=\theta-\eta \cdot \nabla_{\theta} J(\theta) θ=θ−η⋅∇θJ(θ)
缺点:
- 更新速度慢;
- 内存限制,容易超出;
- 无法在线更新模型,即增加训练样本;
1.2 随机梯度下降:
随机梯度下降法(stochastic gradient descent, SGD)根据每一条训练样本x(i)和标签y(i)更新参数:
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i ) ; y ( i ) ) \theta=\theta-\eta \cdot \nabla_{\theta} J\left(\theta ; x^{(i)} ; y^{(i)}\right) θ=θ−η⋅∇θJ(θ;x(i);y(i))
优点:
- 运行速度快;
- 可在线学习;
缺点:
- Loss下降会出现剧烈波动,高方差频繁更新,有很多噪声;
1.3 小批量梯度下降法
每次更新时使用n个小批量训练样本:
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i : i + n ) ; y ( i : i + n ) ) \theta=\theta-\eta \cdot \nabla_{\theta} J\left(\theta ; x^{(i : i+n)} ; y^{(i : i+n)}\right) θ=θ−η⋅∇θJ(θ;x(i:i+n);y(i:i+n))
优点:
1.4 传统梯度下降的挑战:
- 选择一个合适的学习率很困难,太大收敛慢,太小收敛波动;
- 学习率固定不变,不利于收敛;
- 鞍点梯度为0,SGD很难逃离。
由于存在种种的挑战,然后提出了后续各种强化的优化算法。
2. 指数加权平均:
指数加权平均并不是一个优化算法,但是后面的算法都和指数加权平均相关。
以温度为例子,如果要求温度的趋势,也就是求温度的局部平均值,或者滑动平均。但是滑动平均的计算开销较大,所以考虑指数加权平均。
v t = β v t − 1 + ( 1 − β ) θ t v_{t}=\beta v_{t-1}+(1-\beta) \theta_{t} vt=βvt−1+(1−β)θt
v t : v_{t}: vt:t时刻的趋势值;
θ t \theta_{t} θt:t时刻的温度值;
指数加权平均的本质其实是用历史数据来拟合当下数据,距离当前时刻越近的数据,所占权重越大,距离越远的数据,权重越小。
假设上述公式 β = 0.9 , t = 100 \beta=0.9, t=100 β=0.9,t=100,化简后:
v 100 = 0.1 θ 100 + 0.1 × 0.9 θ 99 + 0.1 × ( 0.9 ) 2 θ 98 + 0.1 × ( 0.9 ) 3 θ 97 + 0.1 × ( 0.9 ) 4 θ 96 + … v_{100}=0.1 \theta_{100}+0.1 \times 0.9 \theta_{99}+0.1 \times(0.9)^{2} \theta_{98}+0.1 \times(0.9)^{3} \theta_{97}+0.1 \times(0.9)^{4} \theta_{96}+\dots v100=0.1θ100+0.1×0.9θ99+0.1×(0.9)2θ98+0.1×(0.9)3θ97+0.1×(0.9)4θ96+…
而后面的动量梯度下降其实就是梯度值的指数加权平均。
3. 梯度下降优化算法:
3.1 动量法(Momentum):
利用前面所介绍的指数加权平均,将历史梯度值添加到当前梯度更新向量中。 β \beta β一般选择0.9。
v d W = β v d W + ( 1 − β ) d W v_{d W}=\beta v_{d W}+(1-\beta) d W vdW=βvdW+(1−β)dW
W : = W − a v d W W :=W-a v_{d W} W:=W−avdW
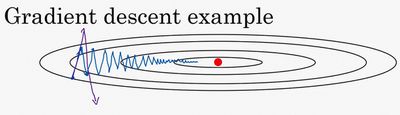
从本质上说,动量法,就像我们从山上推下一个球,球在滚下来的过程中累积动量,变得越来越快(直到达到终极速度,如果有空气阻力的存在,则γ<1)。同样的事情也发生在参数的更新过程中:对于在梯度点处具有相同的方向的维度,其动量项增大,对于在梯度点处改变方向的维度,其动量项减小。因此,我们可以得到更快的收敛速度,同时可以减少摇摆。
3.2 RMSprop(root mean square prop):
同样考虑这张图:
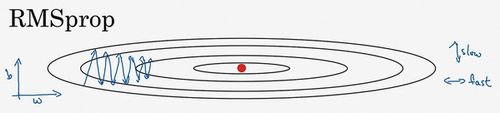
RMSprop能够抑制竖直方向的摆动,加快水平方向的迭代。
S d W = β S d W + ( 1 − β ) d W 2 S_{d W}=\beta S_{d W}+(1-\beta) d W^{2} SdW=βSdW+(1−β)dW2
W : = W − a d W S d W + ϵ W :=W-a \frac{d W}{\sqrt{S_{d W} +\epsilon}} W:=W−aSdW+ϵdW
在公式中我们可以看到,在波动 S d w S_{dw} Sdw较大的地方,将其作为分母会起到抑制的作用,消除摆动。 β \beta β一般设置为0.9, ϵ \epsilon ϵ一般设置为 1 0 − 8 10^{-8} 10−8,可以避免分母为0。
3.3 Adam(Adaptive Moment Estimation)
Adam优化算法本质上就是将Momentum和RMSprop结合在一起。
v d W = β 1 v d W + ( 1 − β 1 ) d W ; v d W corrected = v d W 1 − β 1 t v_{d W}=\beta_{1} v_{d W}+\left(1-\beta_{1}\right) d W; v_{d W}^{\text {corrected }}=\frac{v_{d W}}{1-\beta_{1}^{t}} vdW=β1vdW+(1−β1)dW;vdWcorrected =1−β1tvdW
S d W = β 2 S d W + ( 1 − β 2 ) ( d W ) 2 ; S d W corrected = S d W 1 − β 2 t S_{d W}=\beta_{2} S_{d W}+\left(1-\beta_{2}\right)(d W)^{2}; S_{d W}^{\text {corrected }}=\frac{S_{d W}}{1-\beta_{2}^{t}} SdW=β2SdW+(1−β2)(dW)2;SdWcorrected =1−β2tSdW
W : = W − a v d W corrected S d W corrected + ε W :=W-\frac{a v_{d W}^{\text {corrected }}}{\sqrt{S_{d W}^{\text {corrected }}}+\varepsilon} W:=W−SdWcorrected +εavdWcorrected
β 1 \beta_1 β1:推荐0.9;
β 2 \beta_2 β2:推荐0.99
参考资料:
1. 梯度下降优化算法综述-中文版
2. An overview of gradient descent optimization algorithms
3. 第二周:优化算法 (Optimization algorithms)
4. 从 SGD 到 Adam —— 深度学习优化算法概览(一)
5. Adam那么棒,为什么还对SGD念念不忘 (1) —— 一个框架看懂优化算法
6. Adam那么棒,为什么还对SGD念念不忘 (2)—— Adam的两宗罪
7. 机器学习:各种优化器Optimizer的总结与比较
8. 深度学习最全优化方法总结比较(SGD,Adagrad,Adadelta,Adam,Adamax,Nadam)
9. An overview of gradient descent optimization algorithms