《统计学习方法》第七章: 支持向量机 读书笔记

7.支持向量机（Support vector machines,SVM）

• 是二分类模型。学习策略是间隔最大化
• 包含三种：
  • 线性可分支持向量机：训练数据线性可分，通过硬间隔最大化学习。
  • 线性支持向量机：训练数据近似线性可分（有outlier点），通过软间隔最大化学习
  • 非线性支持向量机：训练数据线性不可分，通过使用核技巧及软间隔最大化学习

7.1 线性可分支持向量机

7.1.2 概念

和感知机的区别

• 感知机利用误分类最小的策略，求得分离超平面，但此时解有无穷多个
• 线性可分支持向量机利用间隔最大化求分离超平面，解是唯一的。

支持向量机的决策函数

• 数据集T,$x\in R^n,y\in \{+1,-1\}$，y为+1时，称实例为正例，反之为负例
• 学习到的分离超平面：
  $$w^{\ast }\cdot x+b^{\ast }=0$$
  相应的决策函数为
  $$f(x)=sign(w^{\ast }\cdot x+b^{\ast })$$

函数间隔

• 超平面(w,b)关于样本点$(x_i,y_i)$的函数间隔为
  $${\hat{r}}_i=y_i(w\cdot x_i+b)$$
• 超平面(w,b)关于样本集T的函数间隔，为所有样本点函数间隔的最小值
  $$\hat{r}=\underset{i=1,2,\cdots ,N}{\min }{\hat{r}}_i$$

几何间隔
令$||w||=1$

• 超平面(w,b)关于样本点$(x_i,y_i)$的几何间隔为
  $$r_i=y_i(\frac{w}{||w||}\cdot x_i+\frac{b}{||w||})$$
• 超平面(w,b)关于样本集T的函数间隔，为所有样本点函数间隔的最小值
  $$r=\underset{i=1,2,\cdots ,N}{\min }{r}_i$$

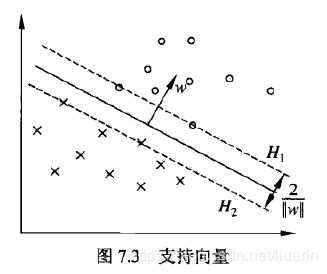
支持向量

• 支持向量：在线性可分的情况下，训练数据集的样本点中与分离超平距离最近的样本点实例称为支持向量。满足：
  $$y_i(w\cdot x_i+b)-1=0$$
• 支撑超平面：正例支持向量所在的超平面，$w\cdot x+b=1$，负例支持向量所在的超平面,$w\cdot x+b=-1$
• 间隔，两个支撑超平面的距离:$\frac{2}{||w||}$
• 支持向量在确定分离超平面中起决定性作用。
  
  函数间隔和几何间隔的关系
• 当$||w||=1$时，函数间隔与集合间隔相等
• 当w,b成比例改变时，函数间隔也按比例改变，但几何间隔不变

硬间隔最大化

• 支持向量机基本想法：对训练数据集找到几何间隔最大的超平面，以充分大的确认度对训练数据进行分类
• 硬间隔最大化：当训练数据线性可分时（即能找到一个线性分离超平面对每个数据都正确的分类），硬性要求每个样本点到超平面的距离>几何间隔

7.1.2 硬间隔最大化数学表示

求解目标
$$\begin{array}{rl}\underset{w,b}{\max }& r\\ s.t.& y_i(\frac{w}{||w||}\cdot x_i+\frac{b}{||w||})⩾r,i=1,2,\cdots ,N\end{array}$$
N是数据集T的数据数目，等价于
$$\begin{array}{rl}\underset{w,b}{\max }& \frac{\hat{r}}{||w||}\\ s.t.& y_i(w\cdot x_i+b)⩾\hat{r},i=1,2,\cdots ,N\end{array}$$
由于$\hat{r}$可以根据w,b的比例改变而改变，那么取$\hat{r}=1$,上述问题等价于
$$\begin{array}{rl}\underset{w,b}{\min }& \frac{1}{2}||w|{|}^2\\ s.t.& y_i(w\cdot x_i+b)-1⩾0,i=1,2,\cdots ,N\end{array}$$

• 由于目标函数 $\frac{1}{2}||w|{|}^2$是二次凸函数，不等式约束$y_i(w\cdot x_i+b)-1⩾0$是仿射函数也是凸函数，有凸集；上述问题称为凸二次规划问题。
• 此时$w,b$有唯一解

拉格朗日函数
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^N{\alpha }_i[y_i(w\cdot x_i+b)]+\sum _{i=1}^N{\alpha }_i$$
其中${\alpha }_i⩾0$，原问题为
$$\underset{w,b}{\min }\underset{\alpha }{\max }L(w,b,\alpha )$$
拉格朗日对偶问题
$$\underset{\alpha }{\max }\underset{w,b}{\min }L(w,b,\alpha )$$

• 对$w,b$求导,得到最小值$L(\alpha )$
  $$\begin{array}{rl}\frac{\partial L(w,b,\alpha )}{\partial w}& =w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0\\ \frac{\partial L(w,b,\alpha )}{\partial b}& =-\sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$
• 带入L得到$L(\alpha )$
  $$\begin{array}{rl}L(\alpha )& =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^N{\alpha }_i{y}_i(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j)\cdot x_i-\sum _{i=1}^N{\alpha }_i{y}_{i}b+\sum _{i=1}^N{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\end{array}$$
  此时对偶问题转为
  $$\begin{array}{rl}\underset{\alpha }{\max }& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$
• 求使$L(\alpha )$最大的最优解${\alpha }^{\ast }$
  根据下文的最小序列算法求解最优${\alpha }^{\ast }$值
• 根据最优解${\alpha }^{\ast }$，及互补松弛条件${\alpha }_i^{\ast }[y_i(w\cdot x_i+b)-1]=0$，得到$w^{\ast },b^{\ast }$
  • 当${\alpha }_i^{\ast }>0$时,$y_i(w\cdot x_i+b)-1=0$，此时样本点为支持向量
  • 当$y_i(w\cdot x_i+b)-1>0$时，${\alpha }_i^{\ast }=0$,样本点不是支持向量机.
    找到最优解${\alpha }^{\ast }$中大于0的分量，设此项index为j，得到：
    $$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\\ b^{\ast }& =y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot x_j\end{array}$$
    求得分离超平面$w^{\ast }\cdot x+b^{\ast }=0$,分类决策函数$f(x)=sign(w^{\ast }\cdot x+b^{\ast })$

最优解

• 获得${\alpha }^{\ast }$
  $$\begin{array}{rl}\underset{\alpha }{\max }& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$
• 获得$w^{\ast },b^{\ast }$（找到最优解${\alpha }^{\ast }$中大于0的分量，设此项index为j）
  $$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\\ b^{\ast }& =y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot x_j\end{array}$$

对于$\alpha$向量，支持向量($y_i(w\cdot x_i+b)=1$)对应的${\alpha }_i>0$，其他样本($y_i(w\cdot x_i+b)>1$)对应的${\alpha }_i=0$。所以对于$w^{\ast }={\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$及$b^{\ast }=y_j-{\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot c_j$值，只由${\alpha }_i̸=0$的样本决定，即支持向量决定。

7.2线性支持向量机

• 对于一些近似线性可分数据，由于存在一些特异点，模型不能把所有的样本都分类正确。

7.2.1软件隔最大化概念

• 所有样本点的函数间隔不能都满足大于样本集的函数间隔这一条件。
• 所以硬间隔最大化需要修改为软间隔最大化。即对每个样本点引进一个松弛变量${\epsilon }_i⩾0$
  $$\begin{array}{rl}\underset{w,b}{\min }& \frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\epsilon }_i\\ s.t.& y_i(w\cdot x_i+b)⩾1-{\epsilon }_i,i=1,2,\cdots ,N\\ & {\epsilon }_i⩾0,i=1,2,\cdots ,N\end{array}$$
• 其中${\epsilon }_i⩾0$是松弛变量；$C⩾0$是惩罚参数，表示对松弛变量的支付代价。
• 最小化的目标是，使$\frac{1}{2}||w|{|}^2$尽可能小，即间隔尽量大，同时使误分类点的个数尽量小。
• 此时w有唯一解，b的解存在一个区间
• 线性支持向量机包含线性可分向量机（${\epsilon }_i=0$）

7.2.3 软间隔最大化数学表示

原问题
$$\begin{array}{rl}\underset{w,b}{\min }& \frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\epsilon }_i\\ s.t.& y_i(w\cdot x_i+b)⩾1-{\epsilon }_i,i=1,2,\cdots ,N\\ & {\epsilon }_i⩾0,i=1,2,\cdots ,N\end{array}$$
拉格朗日函数
$$L(w,b,\epsilon ,\alpha ,\mu )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\epsilon }_i-\sum _{i=1}^N{\alpha }_i[y_i(w\cdot x_i+b)-1+{\epsilon }_i]-\sum _{i=1}^N{\mu }_i{\epsilon }_i$$
其中${\alpha }_i⩾0,{\mu }_i⩾0$，原问题为
$$\underset{w,b,\epsilon }{\min }\underset{\alpha ,\mu }{\max }L(w,b,\epsilon ,\alpha ,\mu )$$
拉格朗日对偶问题
$$\underset{\alpha ,\mu }{\max }\underset{w,b,\epsilon }{\min }L(w,b,\epsilon ,\alpha ,\mu )$$
KKT条件

• 对$w,b,\epsilon$求导,得到最小值$L(\alpha ,\mu )$
  $$\begin{array}{rl}\frac{\partial L(w,b,\epsilon ,\alpha ,\mu )}{\partial w}& =w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0\\ \frac{\partial L(w,b,\epsilon ,\alpha ,\mu )}{\partial b}& =-\sum _{i=1}^N{\alpha }_i{y}_i=0\\ \frac{\partial L(w,b,\epsilon ,\alpha ,\mu )}{\partial {\epsilon }_i}& =C-{\alpha }_i-{\mu }_i=0\end{array}$$
  带入L得到
  $$\begin{array}{rl}L(\alpha ,\mu )& =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+C\sum _{i=1}^N{\epsilon }_i-\sum _{i=1}^N{\alpha }_i{y}_i(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j)\cdot x_i-\sum _{i=1}^N{\alpha }_i{y}_{i}b+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{\epsilon }_i\sum _{i=1}^N{\mu }_i{\epsilon }_i\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i+\sum _{i=1}^N(C-{\alpha }_i-{\mu }_i){\epsilon }_i-\sum _{i=1}^N{\alpha }_i{y}_{i}b\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\end{array}$$
  此时对偶问题转为
  $$\begin{array}{rl}\underset{\alpha }{\max }& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\cdots ,N\\ & {\mu }_i⩾0,i=1,2,\cdots ,N\\ & C-{\alpha }_i-{\mu }_i=0,i=1,2,\cdots ,N(\text{即}0⩽{\alpha }_i⩽C)\end{array}$$
• 求使$L(\alpha )$最大的最优解${\alpha }^{\ast }$
  根据下文的最小序列算法求解最优${\alpha }^{\ast }$值
• 根据最优解${\alpha }^{\ast }$，及互补松弛条件${\alpha }_i^{\ast }[y_i(w\cdot x_i+b)-1+{\epsilon }_i]=0$及${\mu }_i{\epsilon }_i=0$，得到$w^{\ast },b^{\ast }$

  • 当$0<{\alpha }_i^{\ast }<C$时,$0<{\mu }_i$,且${\epsilon }_i=0$,此时,$y_i(w\cdot x_i+b)-1=0$.

  • 但${\alpha }_i=C$,此时${\mu }_i=0$,且${\epsilon }_i>0$

    • 如果$0<{\epsilon }_i<1$，$0<y_i(w\cdot x_i+b)<1$样本点在间隔边界和分离超平面之间
    • ${\epsilon }_i=1$，$y_i(w\cdot x_i+b)=0$样本点在分离超平面之上
    • ${\epsilon }_i>1$，$y_i(w\cdot x_i+b)<0$样本点在分离超平面之误分类一侧

  • 当${\alpha }_i=0$,此时${\mu }_i=C$,且${\epsilon }_i=0$,$y_i(w\cdot x_i+b)>1$,此时样本点是被分离超平面明确分类正确的点，对分离超平面的$w,b$不起作用
    

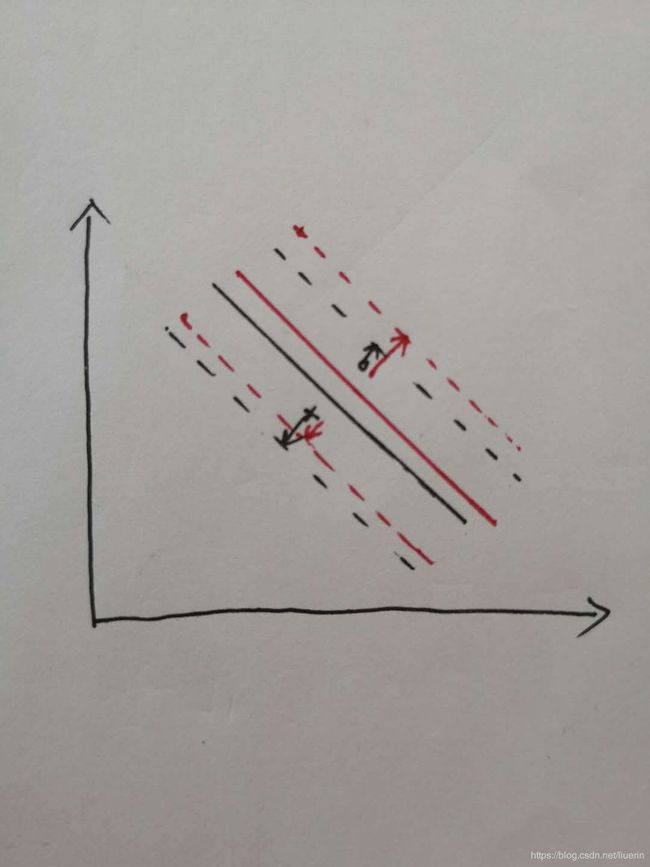
• 我对b有多解的直观理解：w的解是唯一的，$w^{\ast }={\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$，虽说w值唯一，但$\alpha$的解不唯一，$\epsilon$的解不唯一。假如两个点分别为正负样本点，都在间隔平面内，当间隔平面平行移动时，正负样例点距正负间隔平面距离之和是不变的。

找到最优解${\alpha }^{\ast }$中满足$0<{\alpha }_i^{\ast }<C$的分量，设此项index为j，得到：
$$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\\ b^{\ast }& =y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot x_j\end{array}$$
求得分离超平面$w^{\ast }\cdot x+b^{\ast }=0$,分类决策函数$f(x)=sign(w^{\ast }\cdot x+b^{\ast })$
最优解

• 获得${\alpha }^{\ast }$
  $$\begin{array}{rl}\underset{\alpha }{\max }& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & C⩾{\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$
  与线性可分向量机的区别在于${\alpha }_i$的取值范围。
• 获得$w^{\ast },b^{\ast }$（找到最优解${\alpha }^{\ast }$中满足$0<{\alpha }_i^{\ast }<C$的分量，设此项index为j）
  $$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\\ b^{\ast }& =y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot x_j\end{array}$$

对于$w^{\ast }={\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$及$b^{\ast }=y_j-{\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot c_j$值，只由${\alpha }_i̸=0$的样本决定，即支持向量决定。

7.2.3合页损失

线性支持向量机的另一种解释，最小化结构化风险
$$\sum _{i=1}^N[1-y_i(w\cdot x_i+b){]}_{+}+\lambda ||w|{|}^2$$

• 合页损失函数：
  $L(y(w\cdot x+b))=[1-y(w\cdot x+b){]}_{+}$
  其中
  $$[z{]}_{+}=\{\begin{array}{ll}z,& z>0\\ 0,& z⩽0\end{array}$$
  当样本点被正确分类，且函数间隔（确信度）大于1时，损失0；在间隔边界另一侧的样本(分类正确但确信度不够大，或分类错误的样本)，损失为$1-y(w\cdot x+b)$.
• 等价于线性支持向量机
  令$1-y_i(w\cdot x_i+b)={\epsilon }_i$,${\epsilon }_i⩾0$
  那么$\min {\sum }_{i=1}^N[1-y_i(w\cdot x_i+b){]}_{+}+\lambda ||w|{|}^2$等价于$\min {\sum }_{i=1}^N{\epsilon }_i+\lambda ||w|{|}^2$取$\lambda =\frac{1}{2C}$
  等价于$\min C{\sum }_{i=1}^N{\epsilon }_i+\frac{1}{2}||w|{|}^2$

7.3非线性支持向量机

当分类问题非线性，利用核技巧学习

7.3.1 核技巧

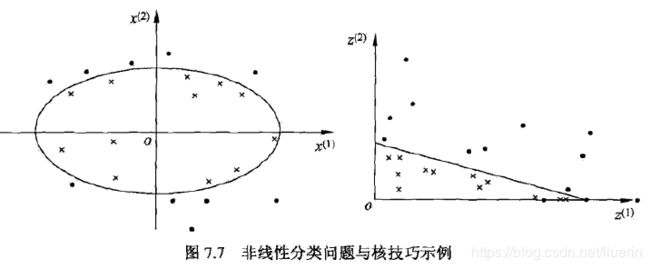
• 非线性可分问题：用一个超曲面将正负例正确分开。
• 使用一个变换将原空间的数据映射到新空间，在新空间里用线性分类学习方法从训练数据中学习模型。
• 当输入空间为欧式空间或离散集合、特征空间为希尔伯特空间时，核函数表示将输入从输入空间映射到特征空间得到的特征向量之间的内积。

核函数数学表达
设X（欧式空间）是输入空间，H为特征空间（希尔伯特），如果存在一个从X到H的映射
$$\varphi (x):x\to H$$
使所有的$x,z\in X$,核函数满足条件
$$K(x,z)=\varphi (x)\cdot \varphi (z)$$
则K(x,z)为核函数，$\varphi (x)$为映射函数

• 通常直接计算K(x,z)

最优解

• 获得${\alpha }^{\ast }$
  $$\begin{array}{rl}\underset{\alpha }{\max }& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)+\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & C⩾{\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$
• 获得$w^{\ast },b^{\ast }$（找到最优解${\alpha }^{\ast }$中满足$0<{\alpha }_i^{\ast }<C$的分量，设此项index为j）
  $$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\varphi (x_i)\\ b^{\ast }& =y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\varphi (x_i)\cdot \varphi (x_j)=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x_j)\end{array}$$
• 分离超平面
  $$\begin{array}{rl}f(x)& =sign(w^{\ast }\cdot \varphi (x)+b^{\ast })\\ & =sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\varphi (x_i)\cdot \varphi (x)+b^{\ast })\\ & =sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x)+b^{\ast })\end{array}$$

7.3.2 常用核函数

• 多项式核函数(polynomial kernel function)
  $$K(x,z)=(x\cdot z+1{)}^p$$
  此时分类决策函数为
  $$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x+1{)}^p+b^{\ast })$$
• 高斯核函数(Gaussian kernel function)
  $$K(x,z)=exp(-\frac{\parallel x-z{\parallel }^2}{2{\sigma }^2})$$
  对应的支持向量机是高斯径向基函数(radius basis function)分类器。此时分类决策函数是
  $$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}exp(-\frac{\parallel x_i-z{\parallel }^2}{2{\sigma }^2})+b^{\ast })$$

7.4线性可分向量机、线性支持向量机、非线性支持向量机的最优解总结

线性可分向量机

• 获得${\alpha }^{\ast }$
  $$\begin{array}{rl}\underset{\alpha }{\max }& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$
• 获得$w^{\ast },b^{\ast }$（找到最优解${\alpha }^{\ast }$中大于0的分量，设此项index为j）
  $$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\\ b^{\ast }& =y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot x_j\end{array}$$

线性支持向量机

• 获得${\alpha }^{\ast }$
  $$\begin{array}{rl}\underset{\alpha }{\max }& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & C⩾{\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$
  与线性可分向量机的区别在于${\alpha }_i$的取值范围。
• 获得$w^{\ast },b^{\ast }$（找到最优解${\alpha }^{\ast }$中满足$0<{\alpha }_i^{\ast }<C$的分量，设此项index为j）
  $$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\\ b^{\ast }& =y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot x_j\end{array}$$

对于$w^{\ast }={\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$及$b^{\ast }=y_j-{\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot c_j$值，只由${\alpha }_i̸=0$的样本决定，即支持向量决定。

非线性支持向量机

• 获得${\alpha }^{\ast }$

$$\begin{array}{rl}\underset{\alpha }{\max }& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)+\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & C⩾{\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$

• 获得$w^{\ast },b^{\ast }$（找到最优解${\alpha }^{\ast }$中满足$0<{\alpha }_i^{\ast }<C$的分量，设此项index为j）
  $$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\varphi (x_i)\\ b^{\ast }& =y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\varphi (x_i)\cdot \varphi (x_j)=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x_j)\end{array}$$

区别

• 线性可分向量机利用硬间隔最大化，${\alpha }_i⩾0$
• 线性支持向量机利用软间隔最大化，$C⩾{\alpha }_i⩾0$
• 非线性向量机利用核技巧，$C⩾{\alpha }_i⩾0$,用$K(x_i,x_j)$代替$x_i\cdot x_j$

7.5序列最小最优化算法（SMO，sequential minimal optimization）

主要针对求解$\alpha$的最优解
$$\begin{array}{rl}\underset{\alpha }{\max }& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)+\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & C⩾{\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$
每次选择两个$\alpha$变量去优化，使所有的$\alpha$变量一直满足${\sum }_{i=1}^N{\alpha }_i{y}_i=0$的条件。

---

KKT条件

原始条件 $$\begin{array}{rl}\underset{x\in R^n}{\min }& f(x)\\ s.t.& c_i(x)⩽0,i=1,2,\cdots ,k\\ & h_j(x)=0,j=1,2,\cdots ,l\end{array}$$ KKT条件 $$\begin{array}{rl}{\nabla }_{x}L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0& \\ {\nabla }_{\alpha }L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0& \\ {\nabla }_{\beta }L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0& \\ {\alpha }_i^{\ast }{c}_i(x^{\ast })=0,& i=1,2,\cdots ,k\\ c_i(x^{\ast })⩽0,& i=1,2,\cdots ,k\\ {\alpha }_i^{\ast }⩾0,& i=1,2,\cdots ,k\\ h_j(x^{\ast })=0,& j=1,2,\cdots ,j\end{array}$$

---