因子图

1 概念

有向图和无向图都可以使得，若干个变量的一个联合概率函数（或全局函数）能够表示成，这些变量的子集上的因子的乘积。

因⼦图比有向图和无向图更显式地表示了这个分解，方法是：在表示变量的结点的基础上，又引入额外结点来表示因子本身。因子图也使我们能够更加清晰地了解分解的细节。

有向图：

P(x)=P(x1)P(x2)P(x3)P(x4|x1,x2,x3)P(x5|x1,x3)P(x6|x4)P(x7|x4,x5)P(x)=P(x1)P(x2)P(x3)P(x4|x1,x2,x3)P(x5|x1,x3)P(x6|x4)P(x7|x4,x5)

用因子图表示，其实就是将相应的函数因子改写：

P(x)=P(x1)P(x2)P(x3)P(x4|x1,x2,x3)P(x5|x1,x3)P(x6|x4)P(x7|x4,x5)=f(x1)f(x2)f(x3)f(x1,x2,x3,x4)f(x1,x3,x5)f(x4,x6)f(x4,x5,x7)P(x)=P(x1)P(x2)P(x3)P(x4|x1,x2,x3)P(x5|x1,x3)P(x6|x4)P(x7|x4,x5)=f(x1)f(x2)f(x3)f(x1,x2,x3,x4)f(x1,x3,x5)f(x4,x6)f(x4,x5,x7)

无向图：

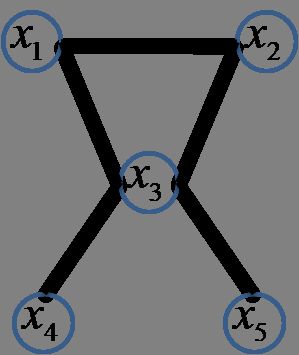
P(x)=1ZψC1(x1,x2,x3)ψC2(x3,x4)ψC3(x3,x5)P(x)=1ZψC1(x1,x2,x3)ψC2(x3,x4)ψC3(x3,x5)

上面的式子是不是也可以看成是多个因子表示的。

因子图：

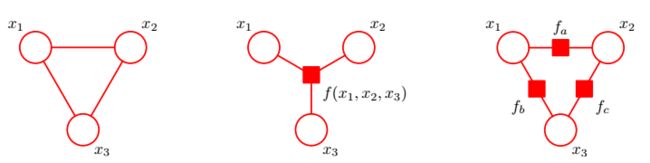
P(x)=fa(x1,x2)fb(x1,x3)fc(x2,x3)P(x)=fa(x1,x2)fb(x1,x3)fc(x2,x3)

2 结构

1）常见的电路图、信号流程图、格子图以及各种框图都属于图模型的范畴；
2）因子图（factor graph，FG）是图模型的一种；
3）因子图的典型代表是Forney-style factor graph，简称 FFG。
4）编码领域、信号处理、人工智能方面的大量算法应用。

一般 FFG 由 结点，边缘，半边缘（只与一个结点连接）组成；
FFG的定义规则如下：
a) 每个因子对应唯一的结点集合；
b) 每个变量对应唯一的边缘或者半边缘；
c) 代表因子 ff 的函数。

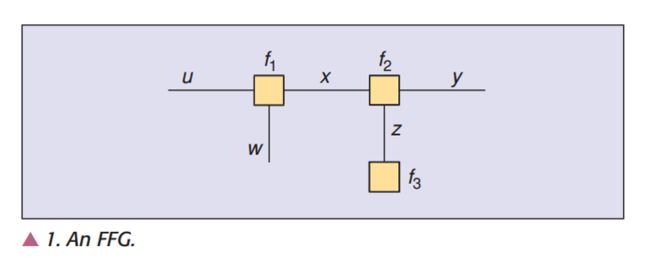
f(u,w,x,y,z)=f1(u,w,x)f2(x,y,z)f3(z)
例：在上图中
3个结点 对应 3个因子：f1，f2，f3f1，f2，f3
2个边缘 对应 2个变量 x,zx,z
3个半边缘 对应 3个变量 u,w,y