深度学习:正则化方法

正则化是机器学习中非常重要并且非常有效的减少泛华误差的技术，特别是在深度学习模型中，由于其模型参数非常多非常容易产生过拟合。因此研究者也提出很多有效的技术防止过拟合，比较常用的技术包括：

1. 参数添加约束，例如L1、L2范数等
2. 训练集合扩充，例如添加噪声、数据变换等
3. Dropout

该文主要介绍深度学习中比较常见几类正则化方法以及常用参数选择，并试图解释其原理。

正则化技术

参数惩罚

通过对模型参数添加惩罚参数来限制模型能力，常用的就是在损失函数基础上添加范数约束。

J˜(θ;,X,y)=J(θ;X,y)+αΩ(θ)

通常情况下，深度学习中只对仿射参数 w 添加约束，对偏置项不加约束。主要原因是偏置项一般需要较少的数据就能精确的拟合。如果添加约束常常会导致欠拟合。

L2正则

参数约束添加L2范数惩罚项，该技术也称之为Weight Decay、岭回归、Tikhonov regularization等。

J˜(w;X,y)=J(w;X,y)+12α||w||2

通过最优化技术，例如梯度相关方法可以很快推导出，参数优化公式为

w=(1−ϵα)w−ϵ∇J(w)

其中 ϵ 为学习率，相对于正常的梯度优化公式，对参数乘上一个缩减因子。

假设J是一个二次优化问题时，模型参数可以进一步表示为 w˜i=λiλi+αwi ，即相当于在原来的参数上添加了一个控制因子，其中 λ 是参数Hessian矩阵的特征值。由此可见
1. 当 λi>>α 时，惩罚因子作用比较小。
2. 当 λi<<α 时，对应的参数会缩减至0

L1正则

对模型参数添加L1范数约束，即

J˜(w;X,y)=J(w;X,y)+α||w||1

如果通过梯度方法进行求解时，参数梯度为

∇J˜(w)=αsign(w)+∇J(w)

特殊情况下，对于二次优化问题，并且假设对应的Hessian矩阵是对角矩阵，可以推导出参数递推公式为 wi=sign(w∗i)max(|w∗i|−αλi,0) ，从中可以看出
当 |w∗i|<αλi 时，对应的参数会缩减到0，这也是和L2正则不同地方。
对比L2优化方法，L2不会直接将参数缩减为0，而是一个非常接近于0的值。

L2 VS L1

主要区别如下：

1. 通过上面的分析，L1相对于L2能够产生更加稀疏的模型，即当L1正则在参数w比较小的情况下，能够直接缩减至0.因此可以起到特征选择的作用，该技术也称之为 LASSO
2. 如果从概率角度进行分析，很多范数约束相当于对参数添加先验分布，其中L2范数相当于参数服从高斯先验分布；L1范数相当于拉普拉斯分布。

范数约束-约束优化问题

从另外一个角度可以将范数约束看出带有参数的约束优化问题。带有参数惩罚的优化目标为

J˜(θ;,X,y)=J(θ;X,y)+αΩ(θ)

带约束的最优问题，可以表示为

minJ(θ;X,y)s.t.Ω(θ)<k

通过KKT条件进行求解时，对应的拉格朗日函数为

L(θ,α;x,y)=J(θ;x,y)+α(Ω(θ)−k)

从约束优化问题也可以进一步看出，L1相对于L2能产生更稀疏的解。

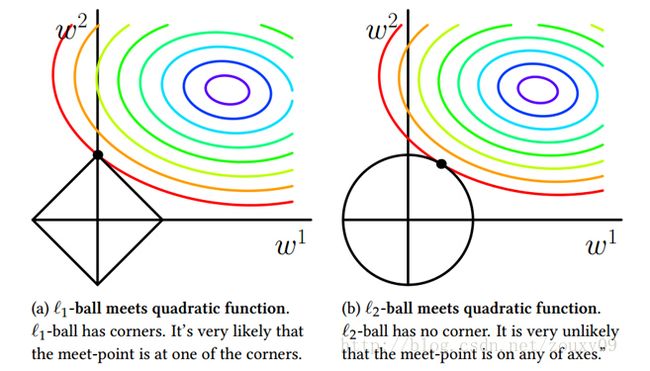
从图中可以看出，L1最优解常常出现在定点处，此时某些维度上的值肯定为0.

数据集合扩充

防止过拟合最有效的方法是增加训练集合，训练集合越大过拟合概率越小。数据集合扩充是一个省时有效的方法，但是在不同领域方法不太通用。
1. 在目标识别领域常用的方法是将图片进行旋转、缩放等（图片变换的前提是通过变换不能改变图片所属类别，例如手写数字识别，类别6和9进行旋转后容易改变类目）
2. 语音识别中对输入数据添加随机噪声
3. NLP中常用思路是进行近义词替换
4. 噪声注入，可以对输入添加噪声，也可以对隐藏层或者输出层添加噪声。例如对于softmax 分类问题可以通过 Label Smoothing技术添加噪声，对于类目0-1添加噪声，则对应概率变成 ϵk,1−k−1kϵ

Dropout

Dropout是一类通用并且计算简洁的正则化方法，在2014年被提出后广泛的使用。
简单的说，Dropout在训练过程中，随机的丢弃一部分输入，此时丢弃部分对应的参数不会更新。相当于Dropout是一个集成方法，将所有子网络结果进行合并，通过随机丢弃输入可以得到各种子网络。例如

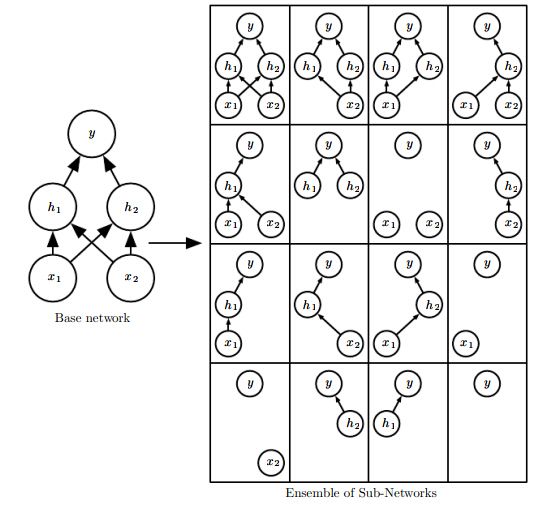
例如上图，通过不同的输入屏蔽相当于学习到所有子网络结构。

因此前向传播过程变成如下形式：

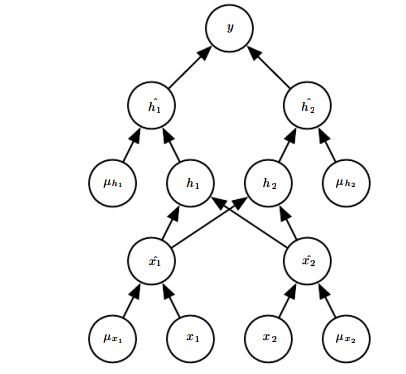
相当于每层输入多了一个屏蔽向量 μ 来控制该层有哪些输入会被屏蔽掉。

经验：原始输入每一个节点选择概率0.8，隐藏层选择概率为0.5

Dropout预测策略

既然Dropout过程类似于集成方法，预测时需要将所有相关模型进行求平均，对于Dropout而言 ∑μp(μ)p(y|x,μ) ，然而遍历所有屏蔽变量不是可能的事情，因此需要一些策略进行预测。
1. 随机选择10-20个屏蔽向量就可以得到一个较好的解。
2. 采用几何平均然后在归一化的思路。

p˜ensemble(y|x)=2d∏μp(y|x,μ)−−−−−−−−−√pensemble(y|x)=p˜ensemble(y|x)∑ip˜ensemble(yi|x)

因此只要估计出 p˜ensemble(y|x) ，2012年Hinton给出一种估计方法，可以只需要一遍前向传播计算最终估计值，模型参数乘上其对应输入单元被包含的概率。该方法也被称为“Weight scaling inference rule”
3. 由于隐藏层节点drop的概率常选取0.5，因此模型权重常常除2即可；也可以在训练阶段将模型参数乘上2

dropout预测实例

假设对于多分类问题，采用softmax进行多分类，假设只有一个隐藏层，输入变量为v，输入的屏蔽变量为 d，d元素选取概率为1/2.
则有

p(Y=y|v,d)=softmax(WT(d∗v)+b)

d*v 代表对应元素相乘，根据几何平均，需要估计 p˜ensemble(y|x)

p˜ensemble(y|v)=2n∏d∈(0,1)np(y|v,d)−−−−−−−−−−−−√=2n∏d∈(0,1)nsoftmax(WT(d∗v)+b)−−−−−−−−−−−−−−−−−−−−−−−−−√=2n∏d∈(0,1)nexp(WTy(d∗v)+b)∑iexp(WTyi(d∗v)+b)−−−−−−−−−−−−−−−−−−−−−−−−⎷=2n∏d∈(0,1)nexp(WTy(d∗v)+b)−−−−−−−−−−−−−−−−−−−−−−√2n∏d∈(0,1)n∑iexp(WTyi(d∗v)+b)−−−−−−−−−−−−−−−−−−−−−−−−−√≈2n∏d∈(0,1)nexp(WTy(d∗v)+b)−−−−−−−−−−−−−−−−−−−−−√≈exp(12n∑d∈(0,1)nWTy(d∗v)+b))≈exp(12WTv+b)

每一步推导基本上都是公式代入的过程，仔细一点看懂没问题。
最后一步需要遍历所有的屏蔽向量d，然而完全遍历并且累加后可以得到2^n-1，在除以2^n，最后得到1/2.
简单以二维举例，则d可以选择的范围包括(0,0)(0,1)(1,0)(1,1)则每一维度都累加了2次，除以4可以得到1/2

DROPOUT的优点

1. 相比于weight decay、范数约束等，该策略更有效
2. 计算复杂度低，实现简单而且可以用于其他非深度学习模型
3. 但是当训练数据较少时，效果不好
4. dropout训练过程中的随机过程不是充分也不是必要条件，可以构造不变的屏蔽参数，也能够得到足够好的解。

其他

半监督学习

通过参数共享的方法，通过共享P(x)和P(y|x)的底层参数能有效解决过拟合。

多任务学习

多任务学习通过多个任务之间的样本采样来达到减少泛化误差。

多任务学习可以将多个相关任务同时学习，并且共享某些参数。多任务可以包括有监督和无监督学习。
对于深度学习而言，可以共享底层隐藏层自然支持多任务学习。

提前停止（Early Stopping）

在模型训练过程中经常出现随着不断迭代，训练误差不断减少，但是验证误差减少后开始增长。
提前停止（Early Stopping）的策略是：在验证误差不在提升后，提前结束训练；而不是一直等待验证误差到最小值。

1. 提前停止策略使用起来非常方便，不需要改变原有损失函数，简单而且执行效率高。
2. 但是它需要一个额外的空间来备份一份参数
3. 提前停止策略可以和其他正则化策略一起使用。
4. 提前停止策略确定训练迭代次数后，有两种策略来充分利用训练数据，一是将全量训练数据一起训练一定迭代次数；二是迭代训练流程直到训练误差小于提前停止策略的验证误差。
5. 对于二次优化目标和线性模型，提前停止策略相当于L2正则化。

参数共享

前提假设：如果两个学习任务比较相似，我们相信两个模型参数比较接近。因此可以加上一些约束条件，例如假设惩罚项 Ω=||wa−wb||2

添加范数惩罚只是参数共享的一种策略，比较通用的策略是可以让部分参数集合保持一致。

集成化方法（Ensemble Methods）

Bagging方法是一种通用的降低泛化误差的方法，通过合并多个模型的结果，也叫作模型平均，高级称呼为 集成化方法。

1. Bagging的策略很多，例如不同初始化方法、不同mini batch选择方法、不同的超参数选择方法。
2. 与之对应的集成方法是Boosting，通过改变样本权重来训练不同模型。

对抗训练

对抗训练的一个主要思路是，总有些输入变量x和x’，他们本身非常相似但是属于不同的类别。如果能单独拿出来特殊对待能够取得比较好的效果。
主要问题是：对抗样本比较难搜集。

总结

正则化是模型优化中非常重要的降低泛化误差的手段，在深度学习中尤其如此，当模型效果不好时，除了调节优化算法本身外，可以尝试L1、L2正则、数据扩充、提前停止和dropout等策略