TensorFlow入门教程：14：噪声数据: 随机分布

前面的文章中主要就线性回归进行了模拟，这篇文章重点讨论一下学习和训练过程中训练数据的问题。

前文中y=3*x + 1的训练数据，直接使用的数据是完全符合的数据，没有任何误差，散点信息如下所示：

绘图代码信息如下

xdata = np.linspace(0,1,100)
ydata = 2 * xdata + 1
plt.scatter(xdata,ydata,color='b')

噪声影响

上述的数据是完美的数据，没有任何干扰情况下的数据，但是往往实际训练模型中很难保证所有数据都是如此。即使是线性回归这么简单的模型也一般不会出现上述类型的实际数据。
就像声音的波形会受到噪声的干扰，最终所得到的叠加的波形一般是输入的数据，在这篇文章中我们也会模拟常见的影响，对数据加上噪声的影响。噪声影响的方式有很多种，比如随机分布与高斯分布。

随机分布

简单来说，对生成的因变量数据加上一个纵向随机小范围的偏移量，主要保证如下的特点：

• 随机性
• 小范围的偏移
• 整体线性不会有变化

随机噪声生成

使用np.random.rand来生成随机噪声

x=np.linspace(0,1,100)
y1=2*x + np.random.rand(*x.shape) + 1

效果与分布

可以看出整体是能够满足：随机/小范围偏移/整体线性趋势明显的效果。这是自然的，因为我们只是加了一个随机的偏移量而已。

再看一下整体分布状况，显示出一定的随机性

示例代码

liumiaocn:Notebook liumiao$ cat basic-operation-9.py 
import numpy      as np
import matplotlib.pyplot as plt

xdata = np.linspace(0,1,100)
ydata = 2 * xdata + np.random.rand(*xdata.shape) + 1
plt.scatter(xdata,ydata,color='b')
plt.title('noise: random.rand')
plt.show()

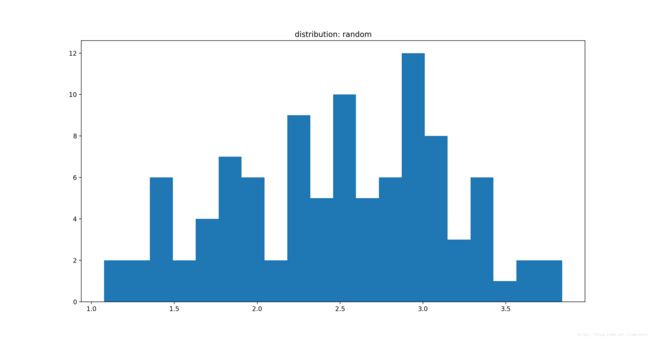
plt.hist(ydata,20)
plt.title('distribution: random')
plt.show()

liumiaocn:Notebook liumiao$

噪声调整

如果对噪声显示的范围有所期待，可以使用很多种方式进行调整，比如在生成的时候指定范围，或者在生成之后简单的乘个幅度，比如：

ydata = 2 * xdata + np.random.rand(*xdata.shape)*0.2 + 1

接下来我们来看一下进行这样调整之后的数据展示与分布状况

示例代码

liumiaocn:Notebook liumiao$ cat basic-operation-10.py 
import numpy      as np
import matplotlib.pyplot as plt

xdata = np.linspace(0,1,100)
ydata = 2 * xdata + np.random.rand(*xdata.shape)*0.2 + 1

plt.subplot(1,2,1)
plt.scatter(xdata,ydata,color='b')
plt.title('noise: random.rand')

plt.subplot(1,2,2)
plt.hist(ydata,20)
plt.title('distribution: random')
plt.show()

liumiaocn:Notebook liumiao$

显示结果

可以看出范围明显收窄，分布仍然呈现随机性的特点

总结

这篇文章我们学习了噪声在训练中的特点，并对随机噪声的生成与分布情况进行了展示，接下来将会对另外一种非常常见的噪声类型（正态分布）进行对比和确认。