排序算法 | 希尔排序算法原理及实现和优化

希尔排序也是一种插入排序算法，也叫作缩小增量排序，是直接插入排序的一种更高效的改进算法。

希尔排序因其设计者希尔（Donald Shell）的名字而得名，该算法在 1959 年被公布。一些老版本的教科书和参考手册把该算法命名为 Shell-Metzner，包含了 Marlene Metzner Norton 的名字，但是 Metzner 说：“我没有为这种算法做任何事，我的名字不应该出现在这个算法的名字中。”

希尔排序在插入排序的基础上，主要通过两点来改进排序算法：

1. 插入排序在对近似有序的数列进行排序时，排序性能会比较好；
2. 插入排序的性能比较低效，即每次只能将数据移动一位。

希尔排序的原理

---

希尔排序的基本思想是：把待排序的数列按照一定的增量分割成多个子数列。但是这个子数列不是连续的，而是通过前面提到的增量，按照一定相隔的增量进行分割的，然后对各个子数列进行插入排序，接着增量逐渐减小，然后仍然对每部分进行插入排序，在减小到1之后直接使用插入排序处理数列。

需要特别强调，这里选择增量的要求是每次都要减少，直至最后一次变为1为止。

下面，我们通过一个实例来理解其实现原理。

在本实例中的首选增量为 n/2，n 为待排序的数列的长度，并且每次的增量都为上一次的 1/2。待排序的数列为 588、392、898、115、306、62、909、902、789、234，有 10 个数。我们首选增量为 10/2 即 5，进行如图 1 所示的分块。

图 1 增量为 5 时的分块

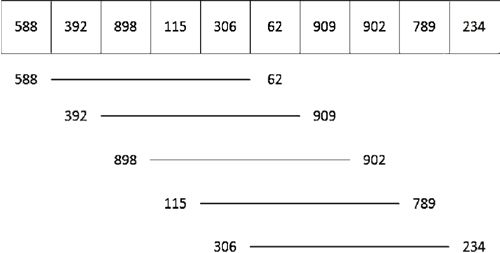
由于增量为 5，所以把原待排序的数列按照增量划分为 5 组，每组实际上都是以增量为间隔的（数组下标为0的元素对应下标为 5 的元素，1 对应 6、2 对应 7，等等）。

之后对每组进行插入排序，其实就是将后一个元素与前一个元素进行比较，看看是否需要交换（当然，还是应该按照插入排序的步骤来进行，就是把后一个元素拿出来，与前一个元素进行比较，看看是否需要移动前面的元素，如果需要移动，则把第 1 个元素后移，然后把拿出来的元素放到前面去；若不需要移动，则不需要进行其他操作）。

分别对每组元素进行插入排序之后的结果如图 2 所示。

图 2 对 5 组数据进行插入排序操作后的结果

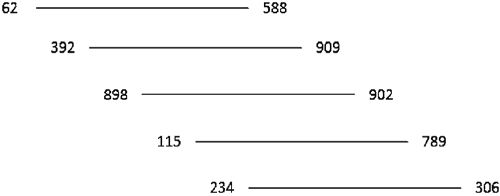
我们发现，实际上在这组数列中只有两组数据进行了移动操作。至此，第 1 趟排序完成。现在的待排序的数列变成了 62、392、898、115、234、588、909、902、789、306。接下来我们该缩减增量了，按照之前的规则，这次的增量应该是 5/2，也就是 2，于是出现了如图 3 所示的划分结果。

图 3 增量为 2 时的第 2 趟划分

现在的待排序的数列的增量为 2，所以每隔一个元素进行分组（也就是数组下标为 0、2、4、6、8 的元素为一组，数组下标为 1、3、5、7、9 的元素为一组），当前的数列被划分为两组，继续对每组数列进行插入排序。

这里就不再复述插入排序的步骤了，大家应该可以轻易地完成对两组数据的插入排序了。第 2 趟排序的结果如图 4 所示。现在的待排序的数列变为 62、115、234、306、789、392、898、588、909、902。

图 4 第 2 趟排序的结果

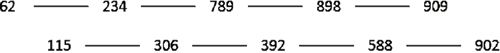
我们发现，每趟排序都会使数组整体更趋于有序了。

接下来对增量继续按照规则除以 2，得到 1，说明这时该对上一趟完成排序的数列进行直接插入排序了。第3趟排序的结果就是最终结果：62、115、234、306、392、588、789、898、902、909，至此希尔排序结束。是不是觉得希尔排序很简单？

希尔排序的实现

---

希尔排序实际上只是对插入排序的一种改进，在算法的实现上，我们需要额外操作的只有对增量的处理及对数列的分块处理。

下面我们一起来看看希尔排序的代码实现：

public class ShellSort {
    public static void main(String[] args) {
        int[] array = {5, 9, 1, 9, 5, 3, 7, 6, 1}; // 待排序数组
        sort(array);
        print(array);
    }

    public static void sort(int array[]) {
        int temp;
        for (int k = array.length / 2; k > 0; k /= 2) {
            for (int i = k; i < array.length; i++) {
                for (int j = i; j >= k; j -= k) {
                    if (array[j - k] > array[j]) {
                        temp = array[j - k];
                        array[j - k] = array[j];
                        array[j] = temp;
                    }
                }
            }
        }
    }

    /**
     * 打印数组
     */
    public static void print(int array[]) {
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + "   ");
        }
        System.out.println();
    }
}

希尔排序的特点及性能

---

其实希尔排序只使用了一种增量的方式去改进插入排序，从上述对该算法的描述及实例中，我们能够清楚地知道实际上希尔排序在内部还是使用插入排序进行处理的。但是这个增量确实有它的意义，不管数列有多长，刚开始时增量会很大，所以每一组待排序的数列的规模会很小，排序会很快。尽管后来数列的规模慢慢变大，但是数列整体已经开始趋于有序了，所以插入排序的速度还是越来越快的。

在时间复杂度上，由于增量的序列不一定，所以时间复杂度也不确定。这在数学上还无法给出确切的结果。我们在上面采用的是每次除以 2 的方式，但是据研究，有以下几种可推荐的序列：

• N/3+1，N/3²+1，N/3³+1……（据说在序列数 N<100 000 时最优）；
• 2^k-1，2^(k-1)-1，2^(k-2)-1……（设 k 为总趟数）；
• 其他的还有质数法等。

对于每次除以 2 的增量选择，希尔排序的最好情况当然是本身有序，每次分区都不用排序，时间复杂度是 O(n)；但是在最坏的情况下仍然每次都需要移动，时间复杂度与直接插入排序在最坏情况下的时间复杂度没什么区别，也是 O(n²)。

但是一般认为希尔排序的平均时间复杂度是 O(n^1.3)。当然，希尔排序的时间复杂度与其增量序列有关，我们知道，一般来说希尔排序会比插入排序快一些，这就足够了。

在希尔排序的实现中仍然使用了插入排序，只是进行了分组，并没有使用其他空间，所以希尔排序的空间复杂度同样是 O(1)，是常量级的。

在希尔排序中会进行分组、排序，所以同样值的元素，其相对位置有可能会发生变化，这是因为同样值的元素若不在一个组中，则有可能后面的元素会被移动到前面。所以希尔排序是不稳定的算法。

希尔排序的适用场景

---

在使用希尔排序时，需要选择合适的增量序列作为排序辅助，而这也是一个比较复杂的抉择。所以希尔排序在实际使用排序时并不常用。

但是作为一个优化排序的思想，我们还是应该好好学习它。