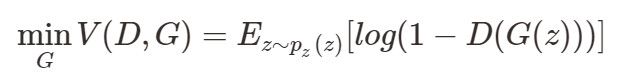生成对抗网络GAN的数学公式的前因后果
Basic Idea of GAN
- Generator G
- Discriminator D
首先定义函数V(G, D)如下:
我们可以通过下面的式子求得最优的生成模型
下面我们来看看原文中几个重要的数学公式描述,首先我们直接上原始论文中的目标公式吧:
上述这个公式说白了就是一个最大最小优化问题,其实对应的也就是上述的两个优化过程。有人说如果不看别的,能达看到这个公式就拍案叫绝的地步,那就是机器学习的顶级专家,哈哈,真是前路漫漫。同时也说明这个简单的公式意义重大。
这个公式既然是最大最小的优化,那就不是一步完成的,其实对比我们的分析过程也是这样的,这里现优化D,然后在取优化G,本质上是两个优化问题,把拆解就如同下面两个公式:
优化D:
优化G:
可以看到,优化D的时候,也就是判别网络,其实没有生成网络什么事,后面的G(z)这里就相当于已经得到的假样本。优化D的公式的第一项,使的真样本x输入的时候,得到的结果越大越好,可以理解,因为需要真样本的预测结果越接近于1越好嘛。对于假样本,需要优化是的其结果越小越好,也就是D(G(z))越小越好,因为它的标签为0。但是呢第一项是越大,第二项是越小,这不矛盾了,所以呢把第二项改成1-D(G(z)),这样就是越大越好,两者合起来就是越大越好。 那么同样在优化G的时候,这个时候没有真样本什么事,所以把第一项直接却掉了。这个时候只有假样本,但是我们说这个时候是希望假样本的标签是1的,所以是D(G(z))越大越好,但是呢为了统一成1-D(G(z))的形式,那么只能是最小化1-D(G(z)),本质上没有区别,只是为了形式的统一。之后这两个优化模型可以合并起来写,就变成了最开始的那个最大最小目标函数了。
所以回过头来我们来看这个最大最小目标函数,里面包含了判别模型的优化,包含了生成模型的以假乱真的优化,完美的阐释了这样一个优美的理论。
在给定G的前提下,我们要取一个合适的D使得V(G, D)能够取得最大值,这就是简单的微积分。
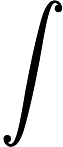
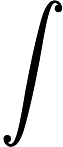
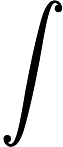
对于这个积分,要取其最大值,我们希望对于给定的x,积分里面的项是最大的,也就是我们希望取到一个最优的 ![]()
![]() D∗ 最大化下面这个式子
D∗ 最大化下面这个式子
在数据给定,G给定的前提下, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 与
与![]()
![]()
![]()
![]()
![]() Pdata(x)与PG(x) 都可以看作是常数,我们可以分别用a,b来表示他们,这样我们就可以得到如下的式子
Pdata(x)与PG(x) 都可以看作是常数,我们可以分别用a,b来表示他们,这样我们就可以得到如下的式子
这样我们就求得了在给定G的前提下,能够使得V(D)取得最大值的D,我们将D代回原来的V(G, D),得到如下的结果
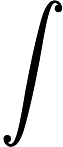
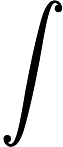
maxV(G,D)=V(G,D∗)=Ex∼Pdata[logPdata(x)Pdata(x)+PG(x)]+Ex∼PG[logPG(x)Pdata(x)+PG(x)]=∫xPdata(x)log12PdataPdata(x)+PG(x)2dx+∫xPG(x)log12PG(x)Pdata(x)+PG(x)2dx=−2log2+KL(Pdata(x)||Pdata(x)+PG(x)2)+KL(PG(x)||Pdata(x)+PG(x)2)
看到这里我们其实就已经推导出了为什么这么衡量是有意义的,因为我们取D使得V(G,D)取得max值,这个时候这个max值是由两个KL divergence构成的,相当于这个max的值就是衡量 ![]()
![]()
![]()
![]()
![]() 与
与![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() PG(x)与Pdata(x) 的差异程度,所以这个时候,我们取
PG(x)与Pdata(x) 的差异程度,所以这个时候,我们取
就能够取到G使得这两种分布的差异性最小,这样自然就能够生成一个和原分布尽可能接近的分布,同时这样也摆脱了计算极大似然估计,所以GAN本质是改变了训练的过程。
由JS散度的性质有,JS散度当且仅当两者相等时去最小值,最小值为0
其中,用到了
1.KL divergence:首先需要一点预备知识,KL divergence,这是统计中的一个概念,是衡量两种概率分布的相似程度,其越小,表示两种概率分布越接近。 对于离散的概率分布,定义如下
对于连续的概率分布,定义如下
2.js散度相似度衡量指标。现有两个分布 P1 和 P2 ,其JS散度公式为: