位姿变换与李群、李代数

　　本博客是在学习高翔《视觉SLAM十四讲》过程中对位姿变换与李群李代数相关知识点做的总结，不涉及公式的证明与推导。

一、位姿变换

1、旋转矩阵与变换矩阵

旋转矩阵是描述刚体旋转最常见的一种形式，而变换矩阵通常是指旋转矩阵与平移向量组成的齐次变换矩阵。对于三维空间的位姿变换，有旋转矩阵：

R=[r1r2r3]=⎡⎣⎢r11r21r31r12r22r32r13r23r33⎤⎦⎥ R = [ r 1 r 2 r 3 ] = [ r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ]

平移向量：

t=[t1t2t3]T t = [ t 1 t 2 t 3 ] T

则旋转矩阵 R R 与平移向量 t t 组成的齐次变换矩阵为：

T=[R0Tt1]=⎡⎣⎢⎢⎢⎢r11r21r310r12r22r320r13r23r330t1t2t31⎤⎦⎥⎥⎥⎥ T = [ R t 0 T 1 ] = [ r 11 r 12 r 13 t 1 r 21 r 22 r 23 t 2 r 31 r 32 r 33 t 3 0 0 0 1 ]

旋转矩阵 R R 是一种单位正交阵，它具有单位正交阵所有的性质：

{r1T⋅r2=r1T⋅r3=r2T⋅r3=0∥r1∥=∥r2∥=∥r3∥=det(R)=1 { r 1 T ⋅ r 2 = r 1 T ⋅ r 3 = r 2 T ⋅ r 3 = 0 ‖ r 1 ‖ = ‖ r 2 ‖ = ‖ r 3 ‖ = d e t ( R ) = 1

重要的是，旋转矩阵的逆等于旋转矩阵的转置，即 R−1=RT R − 1 = R T ，从而有 RR−1=RRT=I R R − 1 = R R T = I 。齐次变换矩阵 T T 的逆为：

T−1=[R−10T−R−1t1]=[RT0T−RTt1] T − 1 = [ R − 1 − R − 1 t 0 T 1 ] = [ R T − R T t 0 T 1 ]

假设我们由坐标系A经过变换矩阵 TABT=[R0Tt1] T B A T = [ R t 0 T 1 ] 得到了坐标系B，那么坐标系B下的点 PBP P B P 可在坐标系A中表示为：

PAP=TABTPBP=[R0Tt1][PBP1]=RPBP+t P A P = T B A T ⁡ P B P = [ R t 0 T 1 ] [ P B P 1 ] = R P B P + t

同样，坐标系A下的点 PAP P A P 可在坐标系B中表示为：

PBP=TBATPAP=TABT−1PAP=[RT0T−RTt1][PAP1]=RTPAP−RTt=RT(PAP−t) P B P = T A B T ⁡ P A P = T B A T − 1 ⁡ P A P = [ R T − R T t 0 T 1 ] [ P A P 1 ] = R T P A P − R T t = R T ( P A P − t )

2、欧拉角与旋转矩阵

欧拉角是描述刚体旋转最直观的一种形式，它往往只用于可视化的人机交互，而无法直接参与运算。

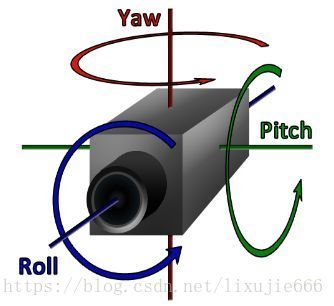
对于三维空间坐标系，我们通常这样规定：

⎧⎩⎨绕 X 轴旋转的角度称为横滚角，Roll绕 Y 轴旋转的角度称为俯仰角，Pitch绕 Z 轴旋转的角度称为偏航角，Yaw { 绕 X 轴旋转的角度称为横滚角，Roll 绕 Y 轴旋转的角度称为俯仰角，Pitch 绕 Z 轴旋转的角度称为偏航角，Yaw

所有的旋转，沿着旋转轴方向顺时针旋转的角度为正，逆时针旋转的角度为负。对于平移，沿着该轴正方向平移的距离为正，负方向平移的距离为负。

设刚体绕着 Z Z 轴旋转 γ γ 角度，那么刚体上所有点的 z z 坐标值不变， x x 与 y y 的坐标值分别变为：

x′=ρcos(θ+γ)=ρ(cosθ⋅cosγ−sinθ⋅sinγ)=x⋅cosγ−y⋅sinγy′=ρsin(θ+γ)=ρ(cosθ⋅sinγ+sinθ⋅cosγ)=x⋅sinγ+y⋅cosγ x ′ = ρ c o s ( θ + γ ) = ρ ( c o s θ ⋅ c o s γ − s i n θ ⋅ s i n γ ) = x ⋅ c o s γ − y ⋅ s i n γ y ′ = ρ s i n ( θ + γ ) = ρ ( c o s θ ⋅ s i n γ + s i n θ ⋅ c o s γ ) = x ⋅ s i n γ + y ⋅ c o s γ

写成矩阵的形式：

⎡⎣⎢x′y′z′⎤⎦⎥=⎡⎣⎢cosγsinγ0−sinγcosγ0001⎤⎦⎥⎡⎣⎢xyz⎤⎦⎥=RZ(γ)⎡⎣⎢xyz⎤⎦⎥ [ x ′ y ′ z ′ ] = [ c o s γ − s i n γ 0 s i n γ c o s γ 0 0 0 1 ] [ x y z ] = R Z ( γ ) [ x y z ]

从而，我们总结出欧拉角与旋转矩阵的关系：

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪Roll：RX(α)=rotx(α)=⎡⎣⎢1000cosαsinα0−sinαcosα⎤⎦⎥Pitch：RY(β)=roty(β)=⎡⎣⎢cosβ0−sinβ010sinβ0cosβ⎤⎦⎥Yaw：RZ(γ)=rotz(γ)=⎡⎣⎢cosγsinγ0−sinγcosγ0001⎤⎦⎥ { Roll： R X ( α ) = rotx ( α ) = [ 1 0 0 0 c o s α − s i n α 0 s i n α c o s α ] Pitch： R Y ( β ) = roty ( β ) = [ c o s β 0 s i n β 0 1 0 − s i n β 0 c o s β ] Yaw： R Z ( γ ) = rotz ( γ ) = [ c o s γ − s i n γ 0 s i n γ c o s γ 0 0 0 1 ]

有了欧拉角与旋转矩阵之间的转换关系，下面举一个简单的例子验证一下：

如上图所示，有位于立方体顶点上的三个坐标系 O1 O 1 、 O2 O 2 、 O3 O 3 ，以及位于立方体中心的点 P P ，立方体的边长分别为6、8、10。下面先进行三个坐标系之间的变换：

• O1→O2 O 1 → O 2 ：

  相对变换： O1 O 1 先沿着坐标轴 O1X1 O 1 X 1 的正方向平移10个单位到达 O2 O 2 ，然后绕着当前位置的 O1Z1 O 1 Z 1 轴顺时针旋转90°，此时新得到的 O1 O 1 与 O2 O 2 坐标系完全重合，即完成了 O1 O 1 到 O2 O 2 的坐标系变换。以上过程可以在MATLAB中用变换矩阵表述为：
  

  T12T=transl(10,0,0)*trotz(pi/2)=⎡⎣⎢⎢⎢10000100001010001⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢0100−100000100001⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢0100−1000001010001⎤⎦⎥⎥⎥ T 2 1 T = transl(10,0,0)*trotz(pi/2) = [ 1 0 0 10 0 1 0 0 0 0 1 0 0 0 0 1 ] [ 0 − 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 ] = [ 0 − 1 0 10 1 0 0 0 0 0 1 0 0 0 0 1 ]

  绝对变换： O1 O 1 先绕着坐标轴 O1Z1 O 1 Z 1 顺时针旋转90°，然后沿着原来 O1X1 O 1 X 1 轴的正方向平移10个单位到达 O2 O 2 ，此时新得到的 O1 O 1 与 O2 O 2 坐标系完全重合，即完成了 O1 O 1 到 O2 O 2 的坐标系变换。以上过程可以在MATLAB中用变换矩阵表述为：
  

  T12T′=transl(10,0,0)*trotz(pi/2)=⎡⎣⎢⎢⎢10000100001010001⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢0100−100000100001⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢0100−1000001010001⎤⎦⎥⎥⎥=T12T T 2 1 T ′ = transl(10,0,0)*trotz(pi/2) = [ 1 0 0 10 0 1 0 0 0 0 1 0 0 0 0 1 ] [ 0 − 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 ] = [ 0 − 1 0 10 1 0 0 0 0 0 1 0 0 0 0 1 ] = T 2 1 T

  你可能会问，两次不同的操作为什么表达式是一样的？原因是这里牵涉到相对变换与绝对变换的区别：
  

  ⎧⎩⎨相对变换：每一步都以新得的坐标系为参考，每一步得到的变换矩阵依次右乘；绝对变换：始终以最初的坐标系为参考，通常是先旋转再平移，每一步得到的变换矩阵依次左乘；相对变换与绝对变换不可同时使用！ { 相对变换：每一步都以新得的坐标系为参考，每一步得到的变换矩阵依次右乘； 绝对变换：始终以最初的坐标系为参考，通常是先旋转再平移，每一步得到的变换矩阵依次左乘； 相对变换与绝对变换不可同时使用！

  当然， O1→O2 O 1 → O 2 的相对变换还可以有很多种操作顺序，比如：
  

  T12T′′=trotz(pi/2)*transl(0,-10,0)=⎡⎣⎢⎢⎢0100−100000100001⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢1000010000100−1001⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢0100−1000001010001⎤⎦⎥⎥⎥=T12T T 2 1 T ″ = trotz(pi/2)*transl(0,-10,0) = [ 0 − 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 ] [ 1 0 0 0 0 1 0 − 10 0 0 1 0 0 0 0 1 ] = [ 0 − 1 0 10 1 0 0 0 0 0 1 0 0 0 0 1 ] = T 2 1 T

  等等，这里不再一一列举。

• O2→O1 O 2 → O 1 ：

  相对变换：
  

  T21T=transl(0,10,0)*trotz(-pi/2)=⎡⎣⎢⎢⎢10000100001001001⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢0−100100000100001⎤⎦⎥⎥⎥=trotz(-pi/2)*transl(-10,0,0)=⎡⎣⎢⎢⎢0−100100000100001⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢100001000010−10001⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢0−1001000001001001⎤⎦⎥⎥⎥ T 1 2 T = transl(0,10,0)*trotz(-pi/2) = [ 1 0 0 0 0 1 0 10 0 0 1 0 0 0 0 1 ] [ 0 1 0 0 − 1 0 0 0 0 0 1 0 0 0 0 1 ] = trotz(-pi/2)*transl(-10,0,0) = [ 0 1 0 0 − 1 0 0 0 0 0 1 0 0 0 0 1 ] [ 1 0 0 − 10 0 1 0 0 0 0 1 0 0 0 0 1 ] = [ 0 1 0 0 − 1 0 0 10 0 0 1 0 0 0 0 1 ]

  绝对变换：
  

  T21T′=transl(0,10,0)*trotz(-pi/2)=⎡⎣⎢⎢⎢10000100001001001⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢0−100100000100001⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢0−1001000001001001⎤⎦⎥⎥⎥=T21T T 1 2 T ′ = transl(0,10,0)*trotz(-pi/2) = [ 1 0 0 0 0 1 0 10 0 0 1 0 0 0 0 1 ] [ 0 1 0 0 − 1 0 0 0 0 0 1 0 0 0 0 1 ] = [ 0 1 0 0 − 1 0 0 10 0 0 1 0 0 0 0 1 ] = T 1 2 T

  相信这些表达式的意义都很容易理解，接下来验证一下 T12T T 2 1 T 与 T21T T 1 2 T 是不是互逆：
  

  T12TT21T=⎡⎣⎢⎢⎢0100−1000001010001⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢0−1001000001001001⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢1000010000100001⎤⎦⎥⎥⎥=I T 2 1 T T 1 2 T = [ 0 − 1 0 10 1 0 0 0 0 0 1 0 0 0 0 1 ] [ 0 1 0 0 − 1 0 0 10 0 0 1 0 0 0 0 1 ] = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] = I

  显然， O1→O2 O 1 → O 2 与 O2→O1 O 2 → O 1 互为逆变换， T12T T 2 1 T 与 T21T T 1 2 T 互逆。其实，由 O1 O 1 到 O2 O 2 的变换矩阵就是对坐标系 O2 O 2 在坐标系 O1 O 1 中位姿的一种描述，即 T12T T 2 1 T 描述了 O2 O 2 在 O1 O 1 中的位置和姿态。同理， T21T T 1 2 T 描述了 O1 O 1 在 O2 O 2 中的位置和姿态。那么，我们已经知道了点 P P 在 O1 O 1 坐标系下的坐标为 P1P=(5,4,3)T P 1 P = ( 5 , 4 , 3 ) T ，坐标系 O1 O 1 在坐标系 O2 O 2 下的位姿为 T21T T 1 2 T ，顺理成章地，我们就可以求得点 P P 在 O2 O 2 坐标系下的坐标为：
  

  P2P=T21TP1P=⎡⎣⎢⎢⎢0−1001000001001001⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢5431⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢4531⎤⎦⎥⎥⎥ P 2 P = T 1 2 T ⁡ P 1 P = [ 0 1 0 0 − 1 0 0 10 0 0 1 0 0 0 0 1 ] [ 5 4 3 1 ] = [ 4 5 3 1 ]

  很显然，结果跟事实是一致的。

• O2↔O3 O 2 ↔ O 3 ：
  

  T23T=transl(8,0,6)*troty(pi)=troty(pi)*transl(-8,0,-6)=⎡⎣⎢⎢⎢−1000010000−108061⎤⎦⎥⎥⎥T32T=transl(8,0,6)*troty(pi)=troty(pi)*transl(-8,0,-6)=⎡⎣⎢⎢⎢−1000010000−108061⎤⎦⎥⎥⎥T23TT32T=⎡⎣⎢⎢⎢−1000010000−108061⎤⎦⎥⎥⎥2=⎡⎣⎢⎢⎢1000010000100001⎤⎦⎥⎥⎥=IP3P=T32TP2P=⎡⎣⎢⎢⎢−1000010000−108061⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢4531⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢4531⎤⎦⎥⎥⎥ T 3 2 T = transl(8,0,6)*troty(pi) = troty(pi)*transl(-8,0,-6) = [ − 1 0 0 8 0 1 0 0 0 0 − 1 6 0 0 0 1 ] T 2 3 T = transl(8,0,6)*troty(pi) = troty(pi)*transl(-8,0,-6) = [ − 1 0 0 8 0 1 0 0 0 0 − 1 6 0 0 0 1 ] T 3 2 T T 2 3 T = [ − 1 0 0 8 0 1 0 0 0 0 − 1 6 0 0 0 1 ] 2 = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] = I P 3 P = T 2 3 T ⁡ P 2 P = [ − 1 0 0 8 0 1 0 0 0 0 − 1 6 0 0 0 1 ] [ 4 5 3 1 ] = [ 4 5 3 1 ]

• O1→O3 O 1 → O 3 ：
  

  T13T=transl(10,8,6)*trotz(pi/2)*troty(pi)=trotz(-pi/2)*trotx(pi)*transl(-8,-10,-6)=T12TT23T=⎡⎣⎢⎢⎢0−100−100000−1010861⎤⎦⎥⎥⎥P3P=T31TP1P=T13T−1P1P=⎡⎣⎢⎢⎢0−100−100000−1081061⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢5431⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢4531⎤⎦⎥⎥⎥ T 3 1 T = transl(10,8,6)*trotz(pi/2)*troty(pi) = trotz(-pi/2)*trotx(pi)*transl(-8,-10,-6) = T 2 1 T ⁡ T 3 2 T = [ 0 − 1 0 10 − 1 0 0 8 0 0 − 1 6 0 0 0 1 ] P 3 P = T 1 3 T ⁡ P 1 P = T 3 1 T − 1 ⁡ P 1 P = [ 0 − 1 0 8 − 1 0 0 10 0 0 − 1 6 0 0 0 1 ] [ 5 4 3 1 ] = [ 4 5 3 1 ]

3、旋转向量与旋转矩阵

旋转向量（或称轴角，Axis-Angle），是一种定义在 R3 R 3 上的三维向量（对于三维空间的旋转来说），它可以描述刚体在三维空间中绕任意旋转轴发生的旋转。旋转向量的方向代表旋转轴的方向，它的模代表旋转的角度。对于一个旋转轴为 n n （ ∥n∥=1 ‖ n ‖ = 1 ），转角为 θ θ 的旋转向量 θn θ n （ θ θ 单位为弧度），它与旋转矩阵 R R 的关系为：

• 旋转向量到旋转矩阵
  

  R=I+sinθn∧+(1−cosθ)n∧2=cosθI+sinθn∧+(1−cosθ)nnT(罗德里格斯公式) (罗德里格斯公式) R = I + s i n θ n ∧ + ( 1 − c o s θ ) n ∧ 2 = c o s θ I + s i n θ n ∧ + ( 1 − c o s θ ) n n T

  这里的 n∧ n ∧ 为 n=[nxnynz]T n = [ n x n y n z ] T 所对应的反对称矩阵：
  

  n∧=⎡⎣⎢0nz−ny−nz0nxny−nx0⎤⎦⎥ n ∧ = [ 0 − n z n y n z 0 − n x − n y n x 0 ]

  且 n∧2=n∧n∧=nnT−I n ∧ 2 = n ∧ n ∧ = n n T − I ， n∧3=−n∧ n ∧ 3 = − n ∧

• 旋转矩阵到旋转向量
  

  ⎧⎩⎨⎪⎪θ=arccos(tr(R)−12)Rn=n { θ = arccos ( tr ( R ) − 1 2 ) R n = n

  其中， tr(R) tr ( R ) 表示旋转矩阵 R R 的迹。旋转轴 n n 其实就是矩阵 R R 特征值1所对应的特征向量。

4、四元数与旋转向量

不得不指出的是，旋转矩阵具有冗余性，而欧拉角和旋转向量都具有奇异性，只有四元数（Quaternions）可以完美地描述一个刚体在三维空间的旋转。

通常，我们用单位四元数 q=qw+qxi+