tensorflow——tf.placeholder用法

https://www.tensorflow.org/api_docs/python/tf/placeholder

tf.placeholder(
    dtype,
    shape=None,
    name=None
)

很简单的函数，仅有3个参数，并且只有第一个dtype是必须参数。
重要的是:这个张量在计算时会产生误差。必须使用feed_dict可选参数将其值提供给Session.run()、Tensor.eval()或Operation.run()。

说白了，只有
Session.run()
Tensor.eval()
Operation.run()
这3个函数才能有feed_dict，才能配合tf.placeholder使用

例子

import tensorflow as tf

# case1:简单点的情况
import tensorflow as tf

# case1:简单点的情况
x = tf.placeholder(tf.float32)
y = x*x

# case2:复杂点的情况
s = tf.placeholder(tf.int16)  # tf默认的整数类型其实是32
t = tf.placeholder(tf.int16)
u = t + s +tf.constant(1, dtype=tf.int16)
v= tf.placeholder(tf.int16)
w = u * v

init = tf.global_variables_initializer
with tf.Session() as sess:
  print(sess.run(y, feed_dict={x: 3.0}))
  print(sess.run(w, feed_dict={s: 1, t: 3, v: 2}))
  writer = tf.summary.FileWriter("logs", sess.graph)  # 文件写在该.py文件同级

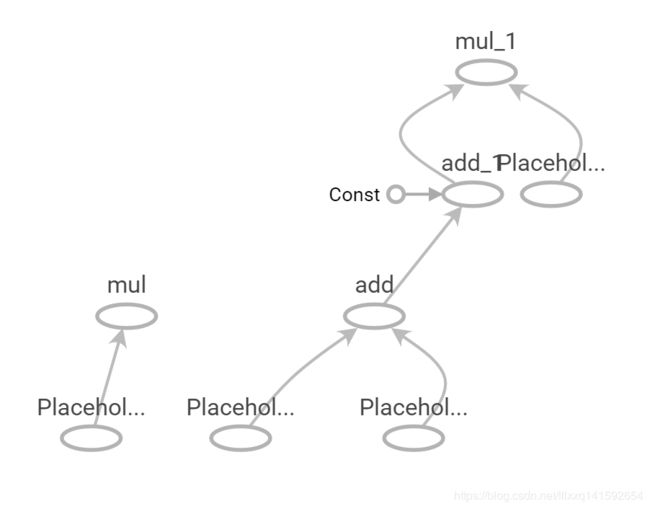
总结：
要运算什么，如y，用sess.run(y)即可，如若y的构成关系中，含有tf.placeholder，则需要在sess.run(y)括号内，加入feed_dict=参数，该参数以字典形式给出构成y的各个placeholder的值。如上边例子中：
case1:y由x构成，则feed_dict中要包含x
case2:w由s,t,v构成，则feed_dict中要包含s,t,v
具体所求量包含什么，要自己去代码中查找，貌似没有一个自动的函数。

ps：图中可以看出，代码中的变量名，并不反映在graph中，想要反映在graph中的变量名，必须在api的name参数中给出。

---

第一次写的

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

#构造输入数据（我们用神经网络拟合x_data和y_data之间的关系）
x_data = np.linspace(-1,1,300)[:, np.newaxis] #-1到1等分300份形成的二维矩阵
noise = np.random.normal(0,0.05, x_data.shape) #噪音，形状同x_data在0-0.05符合正态分布的小数
y_data = np.square(x_data)-0.5+noise #x_data平方，减0.05，再加噪音值
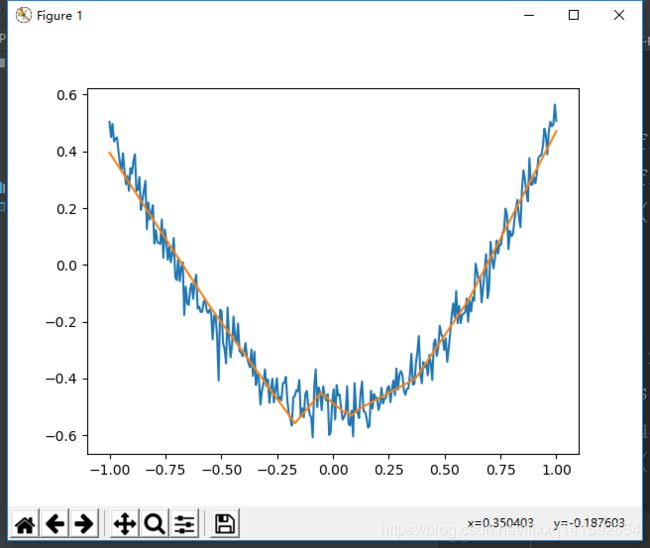
plt.plot(x_data,y_data)
# plt.show()

#输入层（1个神经元）
xs = tf.placeholder(tf.float32, [None, 1]) #占位符，None表示n*1维矩阵，其中n不确定
ys = tf.placeholder(tf.float32, [None, 1]) #占位符，None表示n*1维矩阵，其中n不确定

#隐层（10个神经元）
W1 = tf.Variable(tf.random_normal([1,10])) #权重，1*10的矩阵，并用符合正态分布的随机数填充
b1 = tf.Variable(tf.zeros([1,10])+0.1) #偏置，1*10的矩阵，使用0.1填充
Wx_plus_b1 = tf.matmul(xs,W1) + b1 #矩阵xs和W1相乘，然后加上偏置 shape=[1,10]
output1 = tf.nn.relu(Wx_plus_b1) #激活函数使用tf.nn.relu

#输出层（1个神经元）
W2 = tf.Variable(tf.random_normal([10,1]))
b2 = tf.Variable(tf.zeros([1,1])+0.1)
Wx_plus_b2 = tf.matmul(output1,W2) + b2 # shape=[1, 1]
output2 = Wx_plus_b2

#损失
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys-output2),reduction_indices=[1])) #在第一维上，偏差平方后求和，再求平均值，来计算损失
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) # 使用梯度下降法，设置步长0.1，来最小化损失

#初始化
init = tf.global_variables_initializer() #初始化所有变量
sess = tf.Session()
sess.run(init) #变量初始化

#训练
lxq=[]
for i in range(1000): #训练1000次
    _,loss_value = sess.run([train_step,loss],feed_dict={xs:x_data,ys:y_data}) #进行梯度下降运算，并计算每一步的损失
    # lxq.append(loss_value)
    # if(i%50==0):
    #     print(loss_value) # 每50步输出一次损失

y=sess.run(output2,feed_dict={xs:x_data})
print(y.shape)
for i in range(100):
    print(y[i]-y[i+1])
print(y)
plt.plot(x_data,y)
# plt.plot(lxq)
plt.show()

参考文献
https://www.cnblogs.com/tengge/p/6361005.html