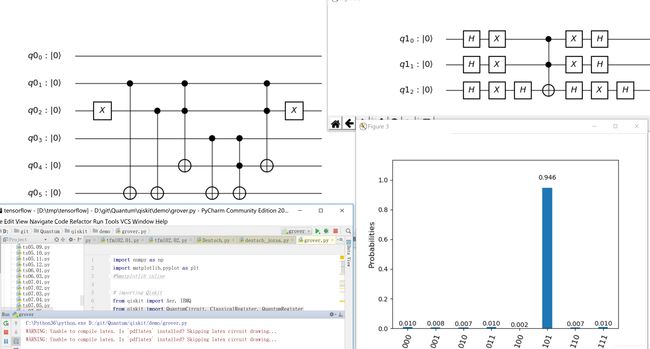
qiskit的grover算法demo
01 资源
01.01 vscode的qiskt插件
IBM的qiskit提供了vscode的插件。插件源码位置:https://github.com/Qiskit/qiskit-vscode
使用参考:
https://marketplace.visualstudio.com/items?itemName=qiskit.qiskit-vscode
01.02 qiskit的demo
https://github.com/Qiskit/qiskit-tutorials
其中算法部分,默认是.ipynb格式,安装 Anaconda 一般会自带对这种格式的支持,也可以直接浏览器打开文件,拷贝代码到本地执行。一般都提供了qiskit模拟和使用实际物理设备试验的方式。使用ibm实际设备调用 IBMQ.load_accounts() 来加载本地保存的IBMQ账号信息(没具体测试怎么使用)。
02 grover算法demo
文档及代码位置:
https://github.com/Qiskit/qiskit-tutorials/blob/master/community/algorithms/grover_algorithm.ipynb
运行此python代码需要安装qiskit库。
pip install qiskit
还需要pdflatex包,我在python3.6.7下没安装成功。也能运行模拟结果。
grover_algorithm.py代码如下:
import numpy as np
import matplotlib.pyplot as plt
#%matplotlib inline
# importing Qiskit
from qiskit import Aer, IBMQ
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import available_backends, execute, register, get_backend, compile
from qiskit.tools import visualization
from qiskit.tools.visualization import circuit_drawer
q = QuantumRegister(6)
qc = QuantumCircuit(q)
qc.x(q[2])
qc.cx(q[1], q[5])
qc.cx(q[2], q[5])
qc.cx(q[3], q[5])
qc.ccx(q[1], q[2], q[4])
qc.ccx(q[3], q[4], q[5])
qc.ccx(q[1], q[2], q[4])
qc.x(q[2])
circuit_drawer(qc)
def black_box_u_f(circuit, f_in, f_out, aux, n, exactly_1_3_sat_formula):
"""Circuit that computes the black-box function from f_in to f_out.
Create a circuit that verifies whether a given exactly-1 3-SAT
formula is satisfied by the input. The exactly-1 version
requires exactly one literal out of every clause to be satisfied.
"""
num_clauses = len(exactly_1_3_sat_formula)
for (k, clause) in enumerate(exactly_1_3_sat_formula):
# This loop ensures aux[k] is 1 if an odd number of literals
# are true
for literal in clause:
if literal > 0:
circuit.cx(f_in[literal-1], aux[k])
else:
circuit.x(f_in[-literal-1])
circuit.cx(f_in[-literal-1], aux[k])
# Flip aux[k] if all literals are true, using auxiliary qubit
# (ancilla) aux[num_clauses]
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
circuit.ccx(f_in[2], aux[num_clauses], aux[k])
# Flip back to reverse state of negative literals and ancilla
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
for literal in clause:
if literal < 0:
circuit.x(f_in[-literal-1])
# The formula is satisfied if and only if all auxiliary qubits
# except aux[num_clauses] are 1
if (num_clauses == 1):
circuit.cx(aux[0], f_out[0])
elif (num_clauses == 2):
circuit.ccx(aux[0], aux[1], f_out[0])
elif (num_clauses == 3):
circuit.ccx(aux[0], aux[1], aux[num_clauses])
circuit.ccx(aux[2], aux[num_clauses], f_out[0])
circuit.ccx(aux[0], aux[1], aux[num_clauses])
else:
raise ValueError('We only allow at most 3 clauses')
# Flip back any auxiliary qubits to make sure state is consistent
# for future executions of this routine; same loop as above.
for (k, clause) in enumerate(exactly_1_3_sat_formula):
for literal in clause:
if literal > 0:
circuit.cx(f_in[literal-1], aux[k])
else:
circuit.x(f_in[-literal-1])
circuit.cx(f_in[-literal-1], aux[k])
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
circuit.ccx(f_in[2], aux[num_clauses], aux[k])
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
for literal in clause:
if literal < 0:
circuit.x(f_in[-literal-1])
# -- end function
def n_controlled_Z(circuit, controls, target):
"""Implement a Z gate with multiple controls"""
if (len(controls) > 2):
raise ValueError('The controlled Z with more than 2 ' +
'controls is not implemented')
elif (len(controls) == 1):
circuit.h(target)
circuit.cx(controls[0], target)
circuit.h(target)
elif (len(controls) == 2):
circuit.h(target)
circuit.ccx(controls[0], controls[1], target)
circuit.h(target)
# -- end function
def inversion_about_average(circuit, f_in, n):
"""Apply inversion about the average step of Grover's algorithm."""
# Hadamards everywhere
for j in range(n):
circuit.h(f_in[j])
# D matrix: flips the sign of the state |000> only
for j in range(n):
circuit.x(f_in[j])
n_controlled_Z(circuit, [f_in[j] for j in range(n-1)], f_in[n-1])
for j in range(n):
circuit.x(f_in[j])
# Hadamards everywhere again
for j in range(n):
circuit.h(f_in[j])
# -- end function
qr = QuantumRegister(3)
qInvAvg = QuantumCircuit(qr)
inversion_about_average(qInvAvg, qr, 3)
circuit_drawer(qInvAvg)
"""
Grover search implemented in Qiskit.
This module contains the code necessary to run Grover search on 3
qubits, both with a simulator and with a real quantum computing
device. This code is the companion for the paper
"An introduction to quantum computing, without the physics",
Giacomo Nannicini, https://arxiv.org/abs/1708.03684.
"""
def input_state(circuit, f_in, f_out, n):
"""(n+1)-qubit input state for Grover search."""
for j in range(n):
circuit.h(f_in[j])
circuit.x(f_out)
circuit.h(f_out)
# -- end function
# Make a quantum program for the n-bit Grover search.
n = 3
# Exactly-1 3-SAT formula to be satisfied, in conjunctive
# normal form. We represent literals with integers, positive or
# negative, to indicate a Boolean variable or its negation.
exactly_1_3_sat_formula = [[1, 2, -3], [-1, -2, -3], [-1, 2, 3]]
# Define three quantum registers: 'f_in' is the search space (input
# to the function f), 'f_out' is bit used for the output of function
# f, aux are the auxiliary bits used by f to perform its
# computation.
f_in = QuantumRegister(n)
f_out = QuantumRegister(1)
aux = QuantumRegister(len(exactly_1_3_sat_formula) + 1)
# Define classical register for algorithm result
ans = ClassicalRegister(n)
# Define quantum circuit with above registers
grover = QuantumCircuit()
grover.add(f_in)
grover.add(f_out)
grover.add(aux)
grover.add(ans)
input_state(grover, f_in, f_out, n)
T = 2
for t in range(T):
# Apply T full iterations
black_box_u_f(grover, f_in, f_out, aux, n, exactly_1_3_sat_formula)
inversion_about_average(grover, f_in, n)
# Measure the output register in the computational basis
for j in range(n):
grover.measure(f_in[j], ans[j])
# Execute circuit
backend = Aer.get_backend('qasm_simulator')
job = execute([grover], backend=backend, shots=1000)
result = job.result()
# Get counts and plot histogram
counts = result.get_counts(grover)
visualization.plot_histogram(counts)
# 下面需要有IBMQ的账号在本地磁盘的配置
IBMQ.load_accounts()
# get ibmq_16_rueschlikon configuration and coupling map
backend = IBMQ.get_backend('ibmq_16_melbourne')
backend_config = backend.configuration()
backend_coupling = backend_config['coupling_map']
# compile the circuit for ibmq_16_rueschlikon
grover_compiled = compile(grover, backend=backend, coupling_map=backend_coupling, seed=1)
grover_compiled_qasm = grover_compiled.experiments[0].header.compiled_circuit_qasm
print("Number of gates for", backend.name(), "is", len(grover_compiled_qasm.split("\n")) - 4)
circuit_drawer(grover)
如有错误之处,欢迎批评指正。QQ群:579809480。