面向初学者的机器学习教程：随机森林

本文内容大致翻译自Random Forests for Complete Beginners，我个人修改并添加了部分内容，若感觉价值不高，请跳过或参阅原文。

这篇文章关注的，更多是思想和理论方法，而不是分类器的使用教程。如果你想要学习算法理论，这篇文章是合适的。但如果你想速成使用方法，这篇文章是不适合你的。

面向初学者的机器学习教程：随机森林

随机森林和决策树的指南

一个很好玩的是：我针对这篇文章制作了一个基于Jupyter Notrbook的动态教程，这里就是playground示例。

现在开始我们的教程！

1.决策树

1.1 什么是决策树

随机森林，故名思义，就是一堆决策树捆绑在了一起。在学习森林之前，我们需要首先从一棵决策树谈起。决策树在分类样本有一定的用途。一个比较经典使用决策树完成的问题就如：“给定一个标记(labelled)数据集，我们应该如何对新样本进行分类(classify)?”

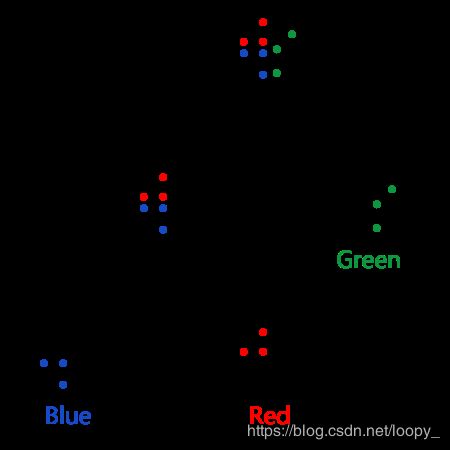
我们使用一个例子来理解这个问题和决策树：观察这个数据集,如果我们需要加入一个新点，并且已知它的X坐标是1，你认为它会是什么颜色?

标记(labelled)数据集: 就是这些分布在二维平面上的点,它们都被标记为了不同的颜色

分类(classify): 给新加入的点分配颜色

你的答案是蓝色,对吗?

让我们仔细分析人是怎么做出这样的决策的。我们通常认为人是在脑子里产生了这样的一个决策树：

这是一个简单的决策树，它在一个决策节点(decision node)中测试(tests)X<2的真假。如果判断为真，就执行左边的分支(branch)并选择蓝色；如果判断为假，就执行右边的分支并选择绿色。数据集上分割效果就是这样的：

那如果我们使用三个颜色来标记这些点呢？

很明显，原来的决策树就不再适用了，而应该变成这样：

• 如果x≥2,那么我们依旧选择绿色。
• 如果x<2,我们就不能直接选择蓝色了，它也可能是红色。

很自然的，我们就需要再添加一个决策节点来形成我们的决策树:

数据集上分割效果就变成了这样：

1.2 训练一个决策树

我们继续使用这个三色数据集

1.2.1 训练根决策节点

首要的任务是确定树的根决策节点。也就是确定：它将测试哪个特征(x坐标还是y坐标？)，测试阈值是多少?例如，我们前面树中的根节点使用x坐标t特征，测试阈值为2

在这里，我们希望决策节点进行“良好”的划分。示例中的上面的根决策节点就做了一个“良好”划分:所有的绿色都在右边，没有绿点在左边。

而这个"良好",是不清晰的，虽然它可以大致理解为尽可能地划分为不同的类，但有没有办法量化为一个数值呢?一种比较好的方法就是基尼系数。（详情可以参看什么是基尼系数）。

我们这里要做的就是找到最"良好"的分割！为了简单起见，我们只是尝试每一个可能的划分并使用最好的一个（具有最高基尼增益系数的那个）。暴力尝试并不是最快方法，但它是最容易理解的。

暴力的尝试划分需要遍历：

• 特征类型（X坐标或Y坐标）。
• 阈值大小（也许是2，3，4…）

比如，如果我们想使用“X坐标”，我们可以遍历以下的阈值:

这时候如果选择0.4，那么左分支有1个红点，右分支有3个蓝点，2个红点，和3个绿点。我们来尝试计算一下基尼增益系数：

整个数据集的基尼杂质系数：
$$\begin{array}{rl}{G}_{inital}& =\sum _{i=1}^{3}p(i)\ast (1-p(i))\\ & =3\ast (\frac{1}{3}\ast \frac{2}{3})\\ & =\frac{2}{3}\end{array}$$

两个分支的基尼杂质系数:
$$G_{left}=0\ast 1+1\ast 0+0\ast 1=0$$
$$\begin{array}{rl}{G}_{right}& =\frac{3}{8}\ast \frac{5}{8}+\frac{2}{8}\ast \frac{6}{8}+\frac{3}{8}\ast \frac{5}{8}\\ & =\frac{21}{32}\end{array}$$

然后就能计算出基尼增益系数：
$$\begin{array}{rl}Gain& =G_{initial}-\frac{1}{9}\ast G_{left}-\frac{8}{9}\ast G_{right}\\ & =\frac{2}{3}-\frac{1}{9}\ast 0+\frac{8}{9}\ast \frac{21}{32}\\ & =0.083\end{array}$$

使用这个方法就能计算出不同测试阈值时的基尼增益系数：


在暴力尝试了x和y的所有阈值后，我们发现x= 2具有最高的基尼增益系数，因此我们使用x=2来完成划分。那么结果就是这样:

1.2.2 训练第二个决策节点

我们注意到左分支里还是杂乱的，于是就需要对左分支的那些点再做一次划分，在类似的一次暴力搜索以后，我们发现“y=2”是这是最好的划分方式：

1.2.3 继续添加决策节点？

是否应该继续添加决策节点呢？生成一个决策树什么时候才需要结束呢？

如果我们继续再最左侧的节点下继续添加一个决策节点,我们会发现不管怎么选取t特征，都不能进一步降低基尼系数（毕竟已经全是蓝点了），那么也就是说：添加决策节点没有意义，它并不能优化决策效果。

因此，我们就停止继续增加决策节点，将这个节点设置为叶子节点，并将其标志为：蓝点类（这些点的共有属性），如果你熟悉树的递归，你就应该知道，这就是“归”的时候了。

然后相同的操作也发现在另两个叶子上，最终得到了我们的结果：

2. 随机森林

终于来到了随机森林。还记得吗?随机森林实际上就是一堆捆绑在一起的决策树。

2.1 装袋算法（Bagging）

装袋算法大概是这样的:

1. 从数据集中随机（均匀、有放回）地抽取n个样本。（这也被称为“自举”）
2. 在这n个样本上训练一棵决策树。
3. 重复t次。

于是就获得了t棵决策树，它们捆到一起就变成了装袋森林！而在参与决策的时候，这片森林会对决策进行投票，最高票的结果就能当选！

2.2 随机森林

袋装决策森林已经非常接近随机森林了，只是有一点不同：

袋装算法只有一个参数t，即决策树数量。但随机森林却有第二个参数特征数量，它表示了在生成一棵决策树时需要使用尝试多少个特征的选择。这是由于往往数据集的特征数量都比2大得多。

如果我们要对一个p个特征的数据集使用随机森林算法。我们在生成一棵决策树时会选择样本容量更少，特征种类更少（通常为$\sqrt{p}$或$\frac{p}{3}$）的一个数据子集。这样做主要是为了随机，使单个树更加独特，减少树之间的相关性，从而提高森林的整体性能。这种技术有时被称为功能袋装（feature bagging）。

3.译者理解

接下来分享一些我的理解。（可跳过）

想象一个p维的空间，里面分布了大量的样本点。我们随机的划出一个子空间，对子空间进行降维，再把其中的这部分样本点取出来，然后在不同维度上综合考虑划分方法，并将这个划分方法记录下来，重复多遍。每个划分方法都反映了在局部样本空间内的各个样本点遵循的规律与特点，而大量的划分方法就能帮助我们获知整个样本空间内的各个样本点遵循的规律与特点。

那么我们就把一个高维度，高容量的样本分析任务给解耦成了易完成的小任务，从而能够解决。

总结

快速回顾一下我们所做的:

• 学习构建随机森林的决策树
• 学习如何通过迭代来寻找最佳划分以训练决策树。
• 发现一个随机森林 = 一群决策树。
• 了解如何将多个树的预测组合在一起。
• 了解到特征袋装决策树和随机森林的区别。

接下来进阶学习需要做的:

• 在真实数据集上使用scikit-learn的 DecisionTreeClassifier和RandomForestClassifier分类器类进行实验。
• 尝试从头编写一个简单的决策树或随机森林实现。
• 阅读关于Gradient Boosted决策树的内容，并尝试强大的梯度增强库XGBoost
• 阅读关于ExtraTrees的内容，并尝试scikit-learn的ExtraTreesClassifie工具。