神经网络——反向传播BP算法应用案例

案例应用（一）——20个样本的两层（单隐藏层）神经网络

知识点：

1、tolist()

链接：http://blog.csdn.net/akagi_/article/details/76382918

2、axis=0：第0轴表示沿着行垂直向下（列）

     axis=1：第1轴表示沿着列的水平方向延伸（行）

3、数据标准化（Normalization）的三种方法：

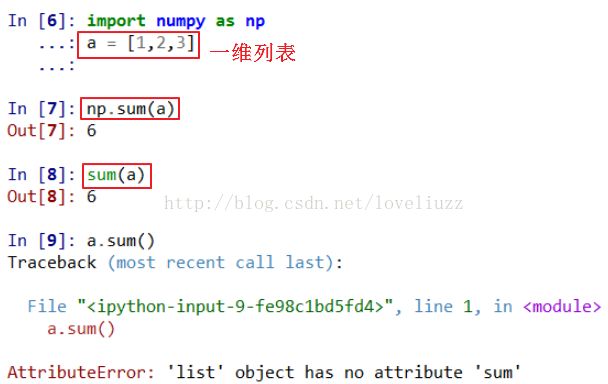
4、python中列表、数组和矩阵的.sum()函数使用区别

链接：http://blog.csdn.net/zhuzuwei/article/details/77766173

（1）列表使用sum, 对1维列表和二维列表，numpy.sum(a)都能将列表a中的所有元素求和并返回，

a.sum()用法是非法的。

       对于1维列表，sum(a)和numpy.sum(a)效果相同，对于二维列表，sum(a)会报错，用法非法。

（2） 在 数组和矩阵中使用sum:  对数组b和矩阵c,代码 b.sum()，np.sum(b),c.sum(),np.sum(c) 都能将b、c中的所有元素求和并返回单个数值。

但是对于二维数组b，代码b.sum(axis=0)指定对数组b对每列求和，b.sum(axis=1)是对每行求和，

返回的都是一维数组（维度降了一维）。

而对应矩阵c，c.sum(axis=0)和c.sum(axis=1)也能实现对列和行的求和，但是返回结果仍是二维矩阵。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu

#BP算法案例（2层神经网络，单隐藏层）——输入样本特征3维，输出二分类，样本20个

import numpy as np
import matplotlib.pyplot as plt

#人数(单位：万人)
population=[20.55,22.44,25.37,27.13,29.45,30.10,30.96,34.06,36.42,38.09,39.13,39.99,41.93,44.59,47.30,52.89,55.73,56.76,59.17,60.63]
#机动车数(单位：万辆)
vehicle=[0.6,0.75,0.85,0.9,1.05,1.35,1.45,1.6,1.7,1.85,2.15,2.2,2.25,2.35,2.5,2.6,2.7,2.85,2.95,3.1]
#公路面积(单位：万平方公里)
roadarea=[0.09,0.11,0.11,0.14,0.20,0.23,0.23,0.32,0.32,0.34,0.36,0.36,0.38,0.49,0.56,0.59,0.59,0.67,0.69,0.79]
#公路客运量(单位：万人)
passengertraffic=[5126,6217,7730,9145,10460,11387,12353,15750,18304,19836,21024,19490,20433,22598,25107,33442,36836,40548,42927,43462]
#公路货运量(单位：万吨)
freighttraffic=[1237,1379,1385,1399,1663,1714,1834,4322,8132,8936,11099,11203,10524,11115,13320,16762,18673,20724,20803,21804]


# In[9]:

samplein = np.mat([population,vehicle,roadarea])    #3*20维矩阵
'''
[[ 20.55  22.44  25.37  27.13  29.45  30.1   30.96  34.06  36.42  38.09
   39.13  39.99  41.93  44.59  47.3   52.89  55.73  56.76  59.17  60.63]
 [  0.6    0.75   0.85   0.9    1.05   1.35   1.45   1.6    1.7    1.85
    2.15   2.2    2.25   2.35   2.5    2.6    2.7    2.85   2.95   3.1 ]
 [  0.09   0.11   0.11   0.14   0.2    0.23   0.23   0.32   0.32   0.34
    0.36   0.36   0.38   0.49   0.56   0.59   0.59   0.67   0.69   0.79]]
'''
sampleinminmax = np.array([samplein.min(axis=1).T.tolist()[0],samplein.max(axis=1).T.tolist()[0]]).transpose() #3*2，对应最大值最小值
'''
[[ 20.55  60.63]
 [  0.6    3.1 ]
 [  0.09   0.79]]
'''

sampleout = np.mat([passengertraffic,freighttraffic])  #2*20
sampleoutminmax = np.array([sampleout.min(axis=1).T.tolist()[0],sampleout.max(axis=1).T.tolist()[0]]).transpose()#2*2，对应最大值最小值

#
#标准化——规范化方法  （x-min)/(max-min）
#3*20
sampleinnorm = (2*(np.array(samplein.T)-sampleinminmax.T[0])/(sampleinminmax.T[1]-sampleinminmax.T[0])-1).transpose()
'''
[[-1.         -0.90568862 -0.75948104 -0.67165669 -0.55588822 -0.52345309
  -0.48053892 -0.3258483  -0.20808383 -0.1247505  -0.07285429 -0.02994012
   0.06686627  0.1996008   0.33483034  0.61377246  0.75548902  0.80688623
   0.92714571  1.        ]
 [-1.         -0.88       -0.8        -0.76       -0.64       -0.4        -0.32
  -0.2        -0.12        0.          0.24        0.28        0.32        0.4
   0.52        0.6         0.68        0.8         0.88        1.        ]
 [-1.         -0.94285714 -0.94285714 -0.85714286 -0.68571429 -0.6        -0.6
  -0.34285714 -0.34285714 -0.28571429 -0.22857143 -0.22857143 -0.17142857
   0.14285714  0.34285714  0.42857143  0.42857143  0.65714286  0.71428571
   1.        ]]
'''
#2*20
sampleoutnorm = (2*(np.array(sampleout.T)-sampleoutminmax.T[0])/(sampleoutminmax.T[1]-sampleoutminmax.T[0])-1).transpose()

#给输出样本添加噪音
noise = 0.03*np.random.rand(sampleoutnorm.shape[0],sampleoutnorm.shape[1])
sampleoutnorm += noise

#超参数
maxepochs = 60000   #最大迭代次数
learnrate = 0.035   #学习率
errorfinal = 0.65*10**(-3)  #最终迭代误差
samnum = 20  #样本数目
indim = 3   #输入特征维度
outdim = 2  #输出特征维度
hiddenunitnum = 8   #隐藏层单元或节点的数目

# 网络参数设计
w1 = 0.5*np.random.rand(hiddenunitnum,indim)-0.1    #8*3维
b1 = 0.5*np.random.rand(hiddenunitnum,1)-0.1        #8*1维
w2 = 0.5*np.random.rand(outdim,hiddenunitnum)-0.1   #2*8维
b2 = 0.5*np.random.rand(outdim,1)-0.1               #2*1维

#激活函数
def logsig(x):
    return 1/(1+np.exp(-x))

errhistory = []

# hiddenout = logsig(np.dot(w1,sampleinnorm)+b1)
# networkout = np.dot(w2, hiddenout) + b2
# err = sampleoutnorm - networkout
# sse = 1/20*np.sum(1/2*err**2)
# dw2 = 1/20*np.dot(err,hiddenout.transpose()) #2*8维
# db2 = 1/20*np.dot(err,np.ones((samnum,1)))
# db3 = 1/20*np.sum(err,axis=1,keepdims=True)

# BP算法遍历
for i in range(maxepochs):
    #前向传播forward propogation

    #隐藏层输出(二维数组/矩阵点积转置与不转置结果相同)
    hiddenout = logsig(np.dot(w1,sampleinnorm)+b1)  #8*20维
    # hiddenout = logsig((np.dot(w1,sampleinnorm).transpose()+b1.transpose())).transpose()

    # 输出层输出
    networkout = np.dot(w2, hiddenout) + b2     #2*20维
    # networkout = (np.dot(w2,hiddenout).transpose()+b2.transpose()).transpose()

    # 误差
    err = sampleoutnorm - networkout    #2*20维
    #sse = sum(sum(err**2))     #这句等价于下面一句
    sse = 1/20*np.sum(1/2*err**2)    #目标函数（cost function）sum对数组里面的所有数据求和，变为一个实数
    errhistory.append(sse)
    if sse < errorfinal:
        break

    #反向传播  backpropogation
    dz2 = err
    dz1 = np.dot(w2.transpose(),dz2)*hiddenout*(1-hiddenout)

    dw2 = 1/20*np.dot(dz2,hiddenout.transpose()) #2*8维
    db2 = 1 / 20 * np.sum(dz2, axis=1, keepdims=True)   #dz2是2*20维，而db2是2*1维，需要做维度转换，按行求和
    # db2 = 1/20*np.dot(err,np.ones((samnum,1)))        #这句与上面一句等价

    dw1 = 1/20*np.dot(dz1,sampleinnorm.transpose())
    db1 = 1/20*np.sum(dz1,axis=1,keepdims=True)
    #db1 = np.dot(dz1,np.ones((samnum,1)))

    w2 += learnrate*dw2
    b2 += learnrate*db2

    w1 += learnrate*dw1
    b1 += learnrate*db1

# 误差曲线图
errhistory10 = np.log10(errhistory)
minerr = min(errhistory10)
plt.plot(errhistory10)
plt.plot(range(0,i+1000,1000),[minerr]*len(range(0,i+1000,1000)))

ax=plt.gca()
ax.set_yticks([-2,-1,0,1,2,minerr])
ax.set_yticklabels([u'$10^{-2}$',u'$10^{-1}$',u'$1$',u'$10^{1}$',u'$10^{2}$',str(('%.4f'%np.power(10,minerr)))])
ax.set_xlabel('iteration')
ax.set_ylabel('error')
ax.set_title('Error History')
#plt.savefig('errorhistory.png',dpi=700)
plt.show()

# 仿真输出和实际输出对比图
hiddenout = logsig((np.dot(w1,sampleinnorm).transpose()+b1.transpose())).transpose()
networkout = (np.dot(w2,hiddenout).transpose()+b2.transpose()).transpose()
diff = sampleoutminmax[:,1]-sampleoutminmax[:,0]
networkout2 = (networkout+1)/2
networkout2[0] = networkout2[0]*diff[0]+sampleoutminmax[0][0]
networkout2[1] = networkout2[1]*diff[1]+sampleoutminmax[1][0]

sampleout = np.array(sampleout)

fig,axes = plt.subplots(nrows=2,ncols=1,figsize=(12,10))
line1, =axes[0].plot(networkout2[0],'k',marker = u'$\circ$')
line2, = axes[0].plot(sampleout[0],'r',markeredgecolor='b',marker = u'$\star$',markersize=9)

axes[0].legend((line1,line2),('simulation output','real output'),loc = 'upper left')

yticks = [0,20000,40000,60000]
ytickslabel = [u'$0$',u'$2$',u'$4$',u'$6$']
axes[0].set_yticks(yticks)
axes[0].set_yticklabels(ytickslabel)
axes[0].set_ylabel(u'passenger traffic$(10^4)$')

xticks = range(0,20,2)
xtickslabel = range(1990,2010,2)
axes[0].set_xticks(xticks)
axes[0].set_xticklabels(xtickslabel)
axes[0].set_xlabel(u'year')
axes[0].set_title('Passenger Traffic Simulation')

line3, = axes[1].plot(networkout2[1],'k',marker = u'$\circ$')
line4, = axes[1].plot(sampleout[1],'r',markeredgecolor='b',marker = u'$\star$',markersize=9)
axes[1].legend((line3,line4),('simulation output','real output'),loc = 'upper left')
yticks = [0,10000,20000,30000]
ytickslabel = [u'$0$',u'$1$',u'$2$',u'$3$']
axes[1].set_yticks(yticks)
axes[1].set_yticklabels(ytickslabel)
axes[1].set_ylabel(u'freight traffic$(10^4)$')

xticks = range(0,20,2)
xtickslabel = range(1990,2010,2)
axes[1].set_xticks(xticks)
axes[1].set_xticklabels(xtickslabel)
axes[1].set_xlabel(u'year')
axes[1].set_title('Freight Traffic Simulation')

#fig.savefig('simulation.png',dpi=500,bbox_inches='tight')
plt.show()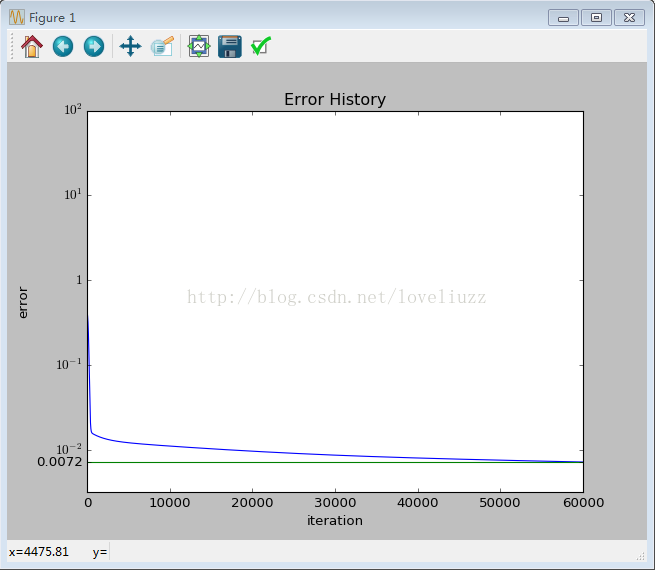

案例应用（二）——神经网络实现线性回归（应用tensorflow）
知识点：

1、tf.Variable 变量（一种特殊数据，在图中有固定位置，不像普通张量可以流动，如w、b等）

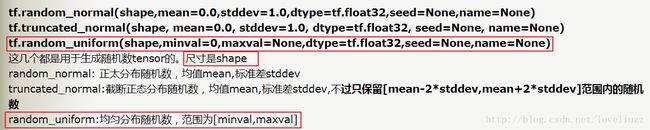
2、tf.random_uniform

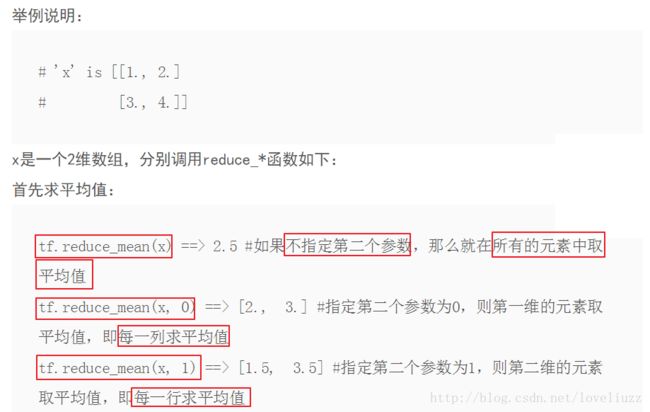
3、tf.reduce_mean()

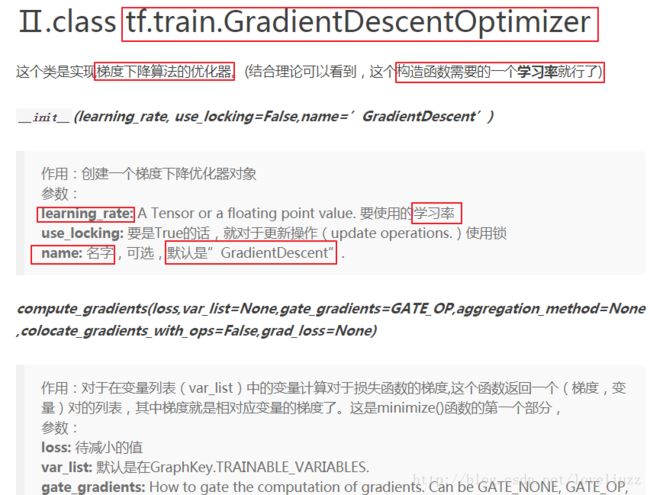
4、优化器Optimizer

详细见链接：http://blog.csdn.net/xierhacker/article/details/53174558

深度学习常见的是对于梯度的优化，也就是说，优化器最后其实就是各种对于梯度下降算法的优化。

5、tf.global_variables_initializer()——初始化所有变量

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu

#神经网络实现线性回归（应用tensorflow）

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

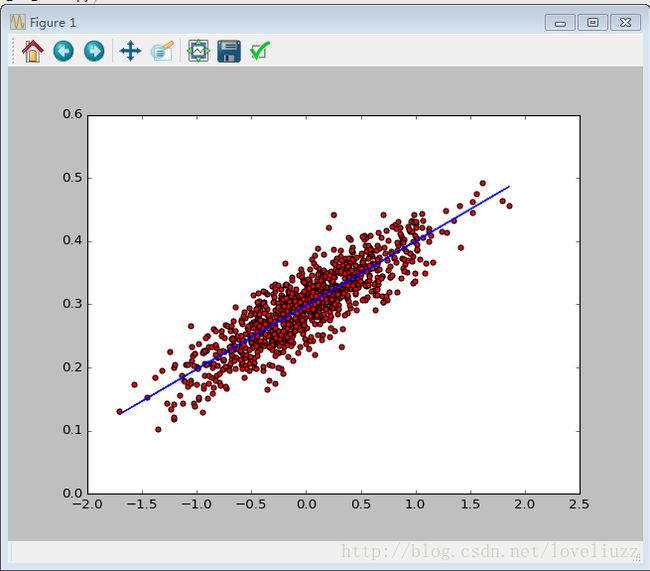
#随即生成1000个点，围绕在直线y=0.1x+0.3范围

num_points = 1000
vectors_set = []
for i in range(num_points):
    x1 = np.random.normal(0.0,0.55)     #生成均值为0.0，方差为0.55的高斯分布
    y1 = x1*0.1+0.3+np.random.normal(0.0,0.03)  #添加一些抖动
    vectors_set.append([x1,y1])

#生成这些样本并画图
x_data = [v[0] for v in vectors_set]
y_data = [v[1] for v in vectors_set]


#由这1000个点逆推线性回归中y=wx+b中的w和b的值
# tf.Variable  变量（一种特殊数据，在图中有固定位置，不像普通张量可以流动，如w、b等）

#生成只有一个元素的w一阶张量，取值是[-1,1]之间的随机数
W = tf.Variable(tf.random_uniform([1],-1.0,1.0),name="W")

#生成只有一个元素的b一阶张量,初始值是0
b = tf.Variable(tf.zeros([1]),name="b")

#前向传播过程——FP
#经过计算得到预估值
y = W * x_data+b

#下面操作完成BP过程
#以预估值y与实际值y_data之间的均方差作为损失值
loss = tf.reduce_mean(tf.square(y-y_data),name="loss")
#采用梯度下降来优化参数，学习率为0.5
optimizer= tf.train.GradientDescentOptimizer(0.5)
#训练过程就是最小化这个误差值
train = optimizer.minimize(loss,name="train")

#建立会话机制
sess = tf.Session()
#初始化所有变量
init = tf.global_variables_initializer()
sess.run(init)
#打印初始化的W和b
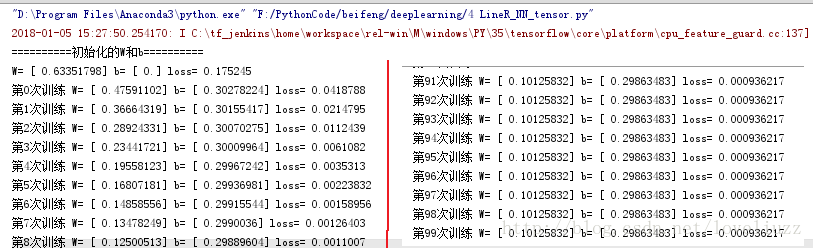
print("==========初始化的W和b==========")
print("W=",sess.run(W),"b=",sess.run(b),"loss=",sess.run(loss))

#执行100次训练
for step in range(100):
    sess.run(train)
    #输出每次训练好的W和b的值
    print("第%d次训练"%step,"W=",sess.run(W),"b=",sess.run(b),"loss=",sess.run(loss))

#画图
plt.scatter(x_data,y_data,c="r")
plt.plot(x_data,sess.run(W)*x_data+sess.run(b))
plt.show()

案例应用（三）——神经网络实现softmax回归手写数字（MNIST）识别案例（应用tensorflow）

1、数据集MNIST

input.py文件具体代码为：

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import gzip
import os
import tempfile

import numpy
from six.moves import urllib
from six.moves import xrange  # pylint: disable=redefined-builtin
import tensorflow as tf
from tensorflow.contrib.learn.python.learn.datasets.mnist import read_data_sets

2、softmax回归

3、模型实现

4、epoch、iteration和batchsize的概念及关系

（1）batchsize：批大小。每次训练在训练集中采取batchsize个样本来训练

（2）iteration：使用batchsize个样本训练一次

（3）epoch：使用训练集中全部样本训练一次

举例：1000个样本，m=1000.假设batchsize=10，则要100次迭代，即：iteration=100

1次epoch。

总结：iteration = m（样本数目）/batchsize

1次epoch遍历，训练样本重复迭代iteration次。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu

#神经网络实现softmax回归手写数字识别案例（应用tensorflow）

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import input_data   #引入MNIST手写数字库

#1、读取数据文件
minist = input_data.read_data_sets("MNIST_data/",one_hot=True)  #标签数据采用独热编码
print(minist)

#下载下来的数据集被分三个子集：
#5.5W行的训练数据集（mnist.train），
#5千行的验证数据集（mnist.validation)
#1W行的测试数据集（mnist.test）。
#每张图片为28x28的黑白图片，所以每行为784维的向量

train_img = minist.train.images
train_label = minist.train.labels

test_img = minist.test.images
test_label = minist.test.labels

print("训练集图片维度:",train_img.shape)
print("训练集标签维度:",train_label.shape)
print("测试集图片维度:",test_img.shape)
print("测试集标签维度:",test_label.shape)
print(minist.train.next_batch)

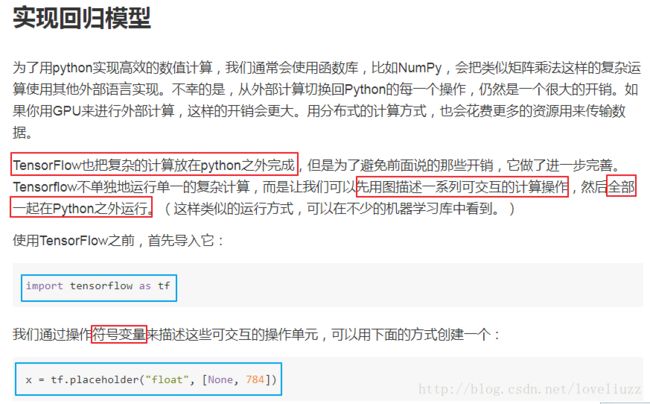
#2、实现softmax回归模型
#placeholder:占位符，MNIST图像每一张784维行向量，None表示任意多维度
x = tf.placeholder("float",[None,784])  #输入值
y = tf.placeholder("float",[None,10])   #输出值（真实值）
#Variable:可修改的张量，可用于计算输入可在计算中被修改,模型的参数可用Variable表示
#用全为零的张量来初始化参数W和b的值
W = tf.Variable(tf.zeros([784,10]),name="W") #想用784维的图片向量乘以W得到一个10维的向量
b = tf.Variable(tf.zeros([1,10]),name="b")    #b  [10]表示10分类
#softmax
#正向传播FP
actv = tf.nn.softmax(tf.matmul(x,W)+b)

#3、模型训练——反向传播BP
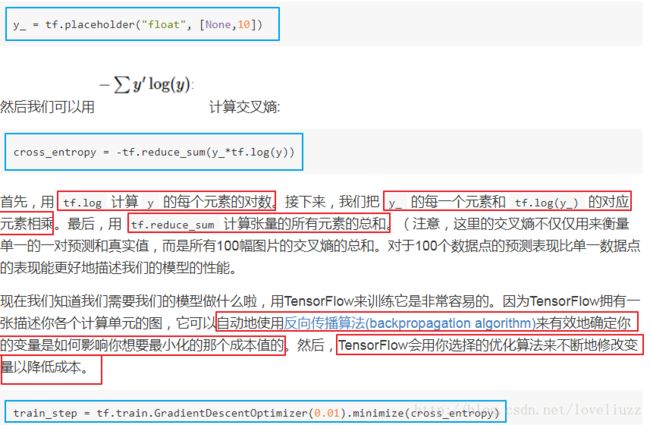
#成本函数用采用交叉熵，y和actv的维度都为[None,10]，reduction_indices表示按行（样本数目）求和
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(actv),reduction_indices=1))
#学习率
learn_rate = 0.01
#使用梯度下降最小化成本函数，训练参数W和b
optm = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost)

#4、模型评估
#tf.arg_max:按行或者按列求出最大值所在的索引值，1：表示按行求最大值
#tf.equal：比较矩阵是否相等，相等返回True，反之，则为false
pred = tf.equal(tf.arg_max(y,1),tf.arg_max(actv,1))
#正确率
accr = tf.reduce_mean(tf.cast(pred,"float"))    #将布尔型的预测转换成float类型

# 运行迭代之前，初始化所有变量
init = tf.initialize_all_variables()

#session会话机制，启动模型
sess = tf.Session()
sess.run(init)

#5、训练迭代
#epochs次数,一个epochs是：使用训练机全部样本训练一次
training_epochs = 50
#批尺寸
batch_size = 100
#全部样本迭代多少次（每隔display_step个epoch）后显示目前状态
display_step = 5

#mini_batch(小批量梯度下降):一次epoch遍历，训练重复迭代iteration次
#举例：1000个样本，batchsize=10,100次迭代iteration，1次epoch
for epoch in range(training_epochs):
    #平均误差
    avg_cost = 0.
    #一个iteration：使用batch_size个样本训练一次，整个数据集要迭代多少次   55000/100
    iteration = int(minist.train.num_examples/batch_size)
    for i in range(iteration):
        # 获取数据集 next_batch获取下一批的数据
        batch_xs,batch_ys = minist.train.next_batch(batch_size)
        #模型训练
        # feeds = {x: batch_xs, y: batch_ys}
        # sess.run(optm, feed_dict=feeds)
        sess.run(optm,feed_dict={x:batch_xs,y:batch_ys})
        avg_cost += sess.run(cost,feed_dict={x:batch_xs,y:batch_ys})/iteration
    #全部样本迭代display_step次进行一次显示当前的损失以及准确率
    if epoch % display_step == 0:
        feeds_train = {x:batch_xs,y:batch_ys}
        feeds_test = {x:minist.test.images,y:minist.test.labels}
        #输出正确率
        train_accr = sess.run(accr,feed_dict=feeds_train)
        test_accr = sess.run(accr,feed_dict=feeds_test)
        print("Epoch:%03d/%03d cost:%.9f train_accr:%.3f test_accr:%.3f"
              %(epoch,training_epochs,avg_cost,train_accr,test_accr))
        print("W:", sess.run(W))
        print("b:", sess.run(b))
        print("*"*20)
print("DONE")

#运行结果：
Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
Datasets(train=, validation=, test=)
训练集图片维度: (55000, 784)
训练集标签维度: (55000, 10)
测试集图片维度: (10000, 784)
测试集标签维度: (10000, 10)
Epoch:000/050 cost:1.176831373 train_accr:0.750 test_accr:0.853
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.03770958  0.08092883 -0.02169059 -0.02095913  0.01895759  0.03047678
  -0.00933352  0.03237541 -0.067066   -0.00597981]]
********************
Epoch:005/050 cost:0.441020201 train_accr:0.920 test_accr:0.895
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.08280824  0.17163301 -0.0378321  -0.06216912  0.04958322  0.17499715
  -0.01772536  0.11357884 -0.26959965 -0.03965827]]
********************
Epoch:010/050 cost:0.383393081 train_accr:0.940 test_accr:0.905
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.11012979  0.20967351 -0.03563696 -0.08677705  0.0589775   0.29126397
  -0.02297049  0.16979647 -0.41462633 -0.05957233]]
********************
Epoch:015/050 cost:0.357317106 train_accr:0.900 test_accr:0.909
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.13363008  0.23510975 -0.0297463  -0.10593367  0.06084103  0.39166909
  -0.02738102  0.21704797 -0.53100455 -0.07697465]]
********************
Epoch:020/050 cost:0.341451609 train_accr:0.860 test_accr:0.912
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.15468769  0.25476453 -0.02259419 -0.12311506  0.06071635  0.48368892
  -0.03233586  0.25885972 -0.63206619 -0.09323484]]
********************
Epoch:025/050 cost:0.330557310 train_accr:0.930 test_accr:0.914
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.17370966  0.26752645 -0.01357625 -0.13669413  0.05872518  0.56635588
  -0.03811283  0.29731038 -0.72129518 -0.10653554]]
********************
Epoch:030/050 cost:0.322338095 train_accr:0.890 test_accr:0.916
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.19247559  0.27978855 -0.00483049 -0.15001576  0.05658424  0.64244586
  -0.04321598  0.33084908 -0.79931128 -0.11982626]]
********************
Epoch:035/050 cost:0.315975045 train_accr:0.910 test_accr:0.917
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.21010886  0.28931084  0.00489429 -0.16127652  0.05297195  0.71280587
  -0.04843408  0.36301994 -0.87218767 -0.1310018 ]]
********************
Epoch:040/050 cost:0.310735948 train_accr:0.920 test_accr:0.918
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.22672468  0.29810169  0.0139696  -0.17220686  0.0496463   0.77722383
  -0.05270857  0.39246288 -0.93745178 -0.14231744]]
********************
Epoch:045/050 cost:0.306350076 train_accr:0.960 test_accr:0.918
W: [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
b: [[-0.24226196  0.30532056  0.02280276 -0.18276472  0.04469334  0.83779395
  -0.05765147  0.42132133 -0.99635118 -0.15290719]]
********************
DONE

案例应用（四）——浅层神经网络（三层，两层隐藏层和一层输出层）

应用tensorflow实现手写数字识别

知识点：

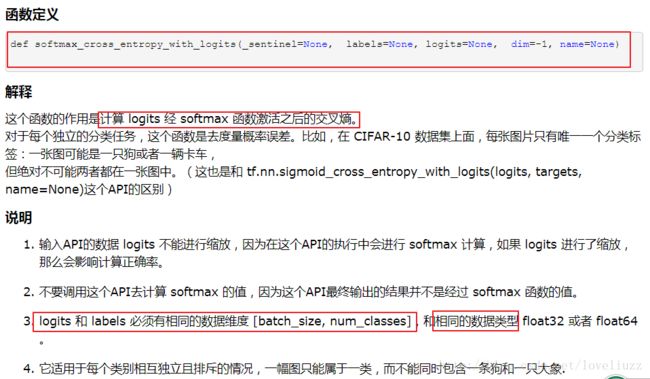
1、softmax_cross_entropy_with_logits()函数

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu

#浅层神经网络(三层，两个隐藏层和一个输出层)实现手写数字识别

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import input_data       #引入MNIST手写数字库

#1、加载数据，在input_data.py中
mnist = input_data.read_data_sets("MNIST_data/",one_hot=True)

#2、神经网络模型
n_hidden_1 = 256    #第一个隐藏层神经单元的数目
n_hidden_2 = 128    #第二个隐藏层神经单元的数目
n_put = 784         #每张图片为28x28的黑白图片，输入像素数目为784
n_classes = 10      #输出的标签label的维度，,0的独热编码为：[1 0 0 0 0 0 0 0 0 0]

#placeholder:占位符，None表示任意多维度
x = tf.placeholder("float",[None,n_put])         #输入值
y = tf.placeholder("float",[None,n_classes])    #输出值

#神经网络模型参数设置，两个隐藏层，初始化参数数据

stddev = 0.1    #标准差

#权重w(用字典存储各层的权重值)
weights = {
    #tf.random_normal 生成一个tensor其中的元素的值服从正态分布
    #tf.random_normal(shape,stddev)，stddev 基于样本估算标准偏差
    #模型的参数可用Variable表示
    "w1":tf.Variable(tf.random_normal([n_put,n_hidden_1],stddev=stddev)),
    "w2":tf.Variable(tf.random_normal([n_hidden_1,n_hidden_2],stddev=stddev)),
    "w3":tf.Variable(tf.random_normal([n_hidden_2,n_classes],stddev=stddev))
}

#偏向b
biases = {
    "b1":tf.Variable(tf.random_normal([n_hidden_1])),
    "b2":tf.Variable(tf.random_normal([n_hidden_2])),
    "b3":tf.Variable(tf.random_normal([n_classes]))
}

#(1)正向传播（FP），只对两个隐藏层做激活函数处理
def multilayer_perceotron(_X,_weights,_biases):
    a1 = tf.nn.sigmoid(tf.add(tf.matmul(_X,_weights["w1"]),_biases["b1"]))
    a2 = tf.nn.sigmoid(tf.add(tf.matmul(a1,_weights["w2"]),_biases["b2"]))
    # 返回的是10个输出,最后的输出层不加激活函数，用softmax进行多分类
    return (tf.matmul(a2,_weights["w3"])+_biases["b3"])

pred = multilayer_perceotron(x,weights,biases)

#(2)反向传播（BP）
#损失函数 softmax_cross_entropy_with_logits，中0.x版本和1.x不同的是1.x要加logits和labels
#softmax_cross_entropy_with_logits函数作用：计算logits经softmax激活后的交叉熵
#logits，它的shape是[batch_size,n_classes] 一般是神经网络的最后一层输出
#labels，它的shape也是[batch_size,n_classes] ，实际输出的标签值
#tf把softmax和cross_entropy计算放在一起用一个函数来实现，提高程序运行速度。
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred,labels=y))
#使用梯度下降最小化成本函数，训练参数W和b
optm = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost)

#3、模型评估
#tf.arg_max:按行或者按列求出最大值所在的索引值，1：表示按行求最大值
#tf.equal：比较矩阵是否相等，相等返回True，反之，则为false
corr = tf.equal(tf.arg_max(pred,1),tf.arg_max(y,1))
#正确率
accr = tf.reduce_mean(tf.cast(corr,"float"))    #将布尔型的corr转换成float类型

# 运行迭代之前，初始化所有变量
init = tf.global_variables_initializer()
#session会话机制，启动模型
sess = tf.Session()
sess.run(init)

#4、执行训练的模型
#epochs次数,一个epochs是：使用训练机全部样本训练一次
training_epochs = 50
#批尺寸
batch_size = 100
#全部样本迭代多少次（每隔display_step个epoch）后显示目前状态
display_step = 5

#mini_batch(小批量梯度下降):一次epoch遍历，训练重复迭代iteration次
#举例：1000个样本，batchsize=10,100次迭代iteration，1次epoch
for epoch in range(training_epochs):
    avg_cost = 0.
    # 一个iteration：使用batch_size个样本训练一次，整个数据集要迭代多少次   55000/100
    iteration = int(mnist.train.num_examples/batch_size)
    for i in range(iteration):
        # 获取数据集 next_batch获取下一批的数据
        batch_xs,batch_ys = mnist.train.next_batch(batch_size)
        # 模型训练
        sess.run(optm,feed_dict={x:batch_xs,y:batch_ys})
        avg_cost += sess.run(cost,feed_dict={x:batch_xs,y:batch_ys})
    avg_cost /= iteration

    # 全部样本迭代duisplay_step次显示一次当前的损失以及准确率
    if epoch % display_step == 0:
        feed_train = {x:batch_xs,y:batch_ys}
        feed_test = {x:mnist.test.images,y:mnist.test.labels}
        #正确率
        train_accr = sess.run(accr,feed_dict=feed_train)
        test_accr = sess.run(accr,feed_dict=feed_test)
        print("Epoch:%03d/%03d cost:%.9f train_accr:%.3f test_accr:%.3f"
              %(epoch,training_epochs,avg_cost,train_accr,test_accr))
        # print("W:",sess.run(weights))
        # print("b:",sess.run(biases))
        print("*"*20)

print ("OPTIMIZATION FINISHED")
#运行结果：
Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
Epoch:000/050 cost:2.413839944 train_accr:0.100 test_accr:0.108
********************
Epoch:005/050 cost:2.256547526 train_accr:0.230 test_accr:0.249
********************
Epoch:010/050 cost:2.208265470 train_accr:0.360 test_accr:0.411
********************
Epoch:015/050 cost:2.151324805 train_accr:0.490 test_accr:0.511
********************
Epoch:020/050 cost:2.081211740 train_accr:0.490 test_accr:0.555
********************
Epoch:025/050 cost:1.994214419 train_accr:0.510 test_accr:0.606
********************
Epoch:030/050 cost:1.889150947 train_accr:0.600 test_accr:0.633
********************
Epoch:035/050 cost:1.768870280 train_accr:0.610 test_accr:0.659
********************
Epoch:040/050 cost:1.639974271 train_accr:0.650 test_accr:0.691
********************
Epoch:045/050 cost:1.510463864 train_accr:0.740 test_accr:0.720
********************
OPTIMIZATION FINISHED