凹凸性和Jensen不等式
参照:
- 凹凸性:https://blog.csdn.net/hqh131360239/article/details/82751791
- Jensen不等式:https://blog.csdn.net/phoenix198425/article/details/78388597
1、凹凸性
1.1、同济大学高等数学定义
\qquad 凹凸函数在同济大学高等数学中的定义符合人们的思维定式。在国际上的定义恰好与同济大学高等数学中的定义相反。
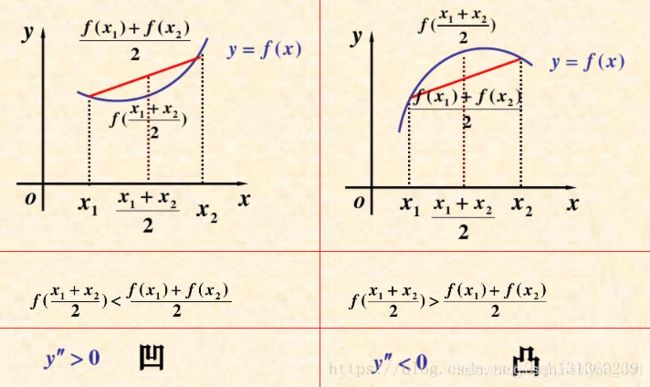
1.2、国际上的定义:
\qquad 国际上的定义刚好与国内的凹凸函数的定义相反。二阶导数大于0,则为凸函数,有极小值;二阶导数小于0,则为凹函数,有极大值(后面涉及到的凹凸函数,均为国际上的定义);
\qquad 例如: e x e^x ex的二阶导数大于0,为凸函数; l o g x log\ x log x的二阶导数小于0,为凹函数;
\qquad 一元函数可以很容易的判断凹凸性,二元函数如何判断凹凸性?用到了海塞矩阵,根据海塞矩阵的正定性,判断凹凸性。
\qquad a)海塞矩阵
A = [ ∂ 2 Z ∂ x 2 ∂ 2 Z ∂ x ∂ y ∂ 2 Z ∂ y ∂ x ∂ 2 Z ∂ y 2 ] A=\left[\begin{matrix} \dfrac{\partial^2Z}{\partial x^2} & \dfrac{\partial^2Z}{\partial x\partial y}\\ \\ \dfrac{\partial^2Z}{\partial y\partial x} & \dfrac{\partial^2Z}{\partial y^2} \end{matrix}\right] A=⎣⎢⎢⎢⎢⎡∂x2∂2Z∂y∂x∂2Z∂x∂y∂2Z∂y2∂2Z⎦⎥⎥⎥⎥⎤
\qquad b)正定矩阵
\qquad 判断海塞矩阵是否为正定矩阵;若所有特征值均不小于零,则称为半正定。 若所有特征值均大于零,则称为正定。特征值怎么求? ∣ λ E − A ∣ = 0 |\lambda E-A|=0 ∣λE−A∣=0,可以求出特征值。若除主对角线上的元素都为0,则主对角线上的值为特征值。 d e t A = ∣ A ∣ = detA=|A|= detA=∣A∣=对角线元素积。
\qquad c)凹凸性判断(正定矩阵为凸函数):
\qquad 例题1: f ( x , y ) = x 2 + 5 y 2 − 6 x + 10 y + 6 f(x,y)=x^2+5y^2-6x+10y+6 f(x,y)=x2+5y2−6x+10y+6
\qquad 海塞矩阵A:
A = [ 2 0 0 10 ] A=\left[\begin{matrix} 2 & 0 \\ \\ 0 & 10 \end{matrix}\right] A=⎣⎡20010⎦⎤
\qquad 所有的特征值均大于0,海塞矩阵为正定矩阵,函数为凸函数。
\qquad 例题2: f ( x , y ) = 10 ( y 2 + 4 x ) 2 + ( 1 − 4 y ) 2 f(x,y)=10(y^2+4x)^2+(1-4y)^2 f(x,y)=10(y2+4x)2+(1−4y)2
\qquad 海塞矩阵A:
A = [ 320 − 160 y − 160 y 120 y 2 − 160 x + 32 ] A=\left[\begin{matrix} 320 & -160y \\ \\ -160y & 120y^2-160x+32 \end{matrix}\right] A=⎣⎡320−160y−160y120y2−160x+32⎦⎤
\qquad 根据特征值,决定函数的凹凸性。
2、Jensen不等式
2.1、特殊形式
\qquad 针对于上述的凸函数,直观意义上的凸函数,有特殊形式:
f ( a + b 2 ) ≥ 1 2 ( f ( a ) + f ( b ) ) = 1 2 f ( a ) + 1 2 f ( b ) f(\dfrac{a+b}{2}) \ge \dfrac{1}{2}(f(a) + f(b)) = \dfrac{1}{2} f(a) + \dfrac{1}{2} f(b) f(2a+b)≥21(f(a)+f(b))=21f(a)+21f(b)
2.2、简单引申
\qquad 针对于上述的凸函数, λ \lambda λ相当于 x 1 x_1 x1的概率, 1 − λ 1-\lambda 1−λ相当于 x 2 x_2 x2的概率,则有:
f ( λ x 1 + ( 1 − λ ) x 2 ) ≥ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 ) f(\lambda x_1 + (1-\lambda) x_2) \ge \lambda f(x_1) + (1-\lambda)f(x_2) f(λx1+(1−λ)x2)≥λf(x1)+(1−λ)f(x2)
2.3、延申拓展
\qquad 针对于上述的凸函数, λ j \lambda_j λj为 y j y_j yj概率,且有 ∑ j λ j = 1 , λ j ≥ 0 \sum\limits_j\lambda_j=1,\lambda_j \ge 0 j∑λj=1,λj≥0,则有:
f ( ∑ j λ j y j ) ≥ ∑ j λ j f ( y j ) f(\sum_j \lambda_jy_j) \ge \sum_j\lambda_jf(y_j) f(j∑λjyj)≥j∑λjf(yj)
2.4、推论
\qquad 若 f ( x ) f(x) f(x) 为区间 R R R上的凸函数, g ( x ) : R → R g(x):R→R g(x):R→R 为一任意函数, X X X 为一取值范围有限的离散变量, E [ f ( g ( X ) ) ] E[f(g(X))] E[f(g(X))] 与 E [ g ( X ) ] E[g(X)] E[g(X)] 都存在,则:
f ( E [ g ( X ) ] ) ≥ E [ f ( g ( X ) ) ] f(E[g(X)]) \ge E[f(g(X))] f(E[g(X)])≥E[f(g(X))]
\qquad 证明:
f ( E [ g ( X ) ] ) = f ( ∑ i = 1 n p i g ( x i ) ) ≥ ∑ i = 1 n p i f ( g ( x i ) ) = E [ f ( g ( X ) ) ] f(E[g(X)]) =f(\sum_{i=1}^np_ig(x_i))\ge \sum_{i=1}^np_if(g(x_i)) = E[f(g(X))] f(E[g(X)])=f(i=1∑npig(xi))≥i=1∑npif(g(xi))=E[f(g(X))]