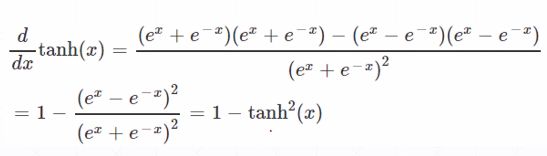pytorch第六课，记录

1、sigmod 的导数
s’ = s(1-s),取值是s ,0-1 (负无穷-正无穷),梯度离散
导数为0，时候梯度得不到更新，梯度离散

a=torch.linspace(-100,100,10)
torch.sigmod(a)

2、tanh，函数和导数 (-1,1)
torch.tanh(a)

from torch.nn import functional as F
F.relu(a)

a=torch.linspace(-1,1,10)##10个数据
torch.tanh(a) torch.sigmod(a)

3、relu, 梯度是1和0，没有梯度离散和爆炸
4 、loss
4.1 mse loss
细节实现，正则实现，差的平方和有根号
loss 差的平方和， 所以mse=torch.norm(y-pred,2).pow(2) # L2正则再平方一下

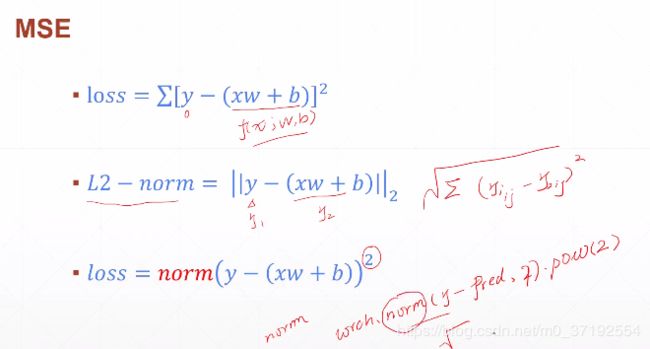
4.2 梯度

autograd 求梯度

x=torch.ones(1)
w=torch.full([1],2)
mse=F.mse_loss(x*w ,torch.ones(1))# (predict,label)
torch.autograd.grad(mse,[w]) #(pred, [w1,w2,w3,…]),

pytorch 中梯度更新的变量 需要加入 requires_grad=True,设置

pytorch 计算一步计算一步图，图也是跟着计算随时更新的

w.requires.grad_() #下划线是 inplace操作表示需要更新w
mse=F.mse_loss(x*w ,torch.ones(1))# (predict,label)，重新计算，更新图
torch.autograd.grad(mse,[w])

loss.backward

x=torch.ones(1)
w=torch.full([1],2)
mse=F.mse_loss(x*w ,torch.ones(1))# (predict,label)

pytorch 前向计算会记录图的路径，所以，backward,可以从后向前传播完成所有需要梯度tensor 的grad计算方法，

不会返回list,会直接附加在每个成员变量 w.grad 下面，返回tensor

w.norm(),#权重的norm， w.grad.norm()#梯度的norm

mse.backward()
w.grad

返回列表[w1.grad,w2.grad…]
直接附加在 变量梯度后面

5 sigmod
每个值是0-1，概率值是1，

softmax 导数，

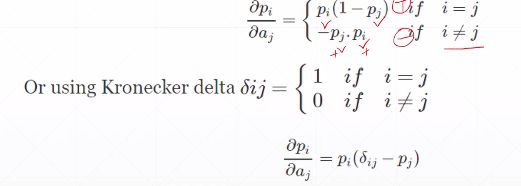
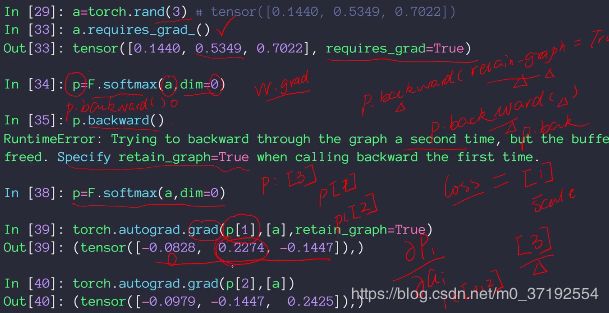
a=torch.rand(3)
p=F.softmax(a,dim=0)
p.backward(retain_graph=True)

# p[1]标量，不能是p列表，[a]是自变量列表，a0 a1 a2

得到的是p[1],对三个变量求得的导数，retain_graph=True，求导图信息不清除，默认清楚本次的图信息

torch.autograd.grad(p[1],[a],retain_graph=True)