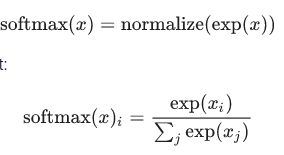Tensorflow-MNIST入门实例

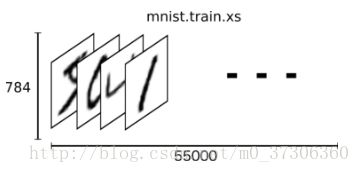
MNIST是一个简单的计算机视觉数据集。 它由像这样的手写数字的图像组成：

它还包括每个图像的标签，告诉我们是哪个数字。 例如，上述图像的标签是5，0，4和1。我们将训练一个模型来查看图像并预测它们的数字。

MNIST 数据集：
数据集下载地址：http://yann.lecun.com/exdb/mnist/

MNIST数据分为三部分：训练数据（mnist.train）55,000个数据点，10,000点测试数据（mnist.test）和5,000点验证数据（mnist.validation）。每个MNIST数据点都有两部分：手写数字的图像和相应的标签。 我们称图像“x”和标签“y”。 训练集和测试集都包含图像及其相应的标签; 例如，训练图像是mnist.train.images，训练标签是mnist.train.labels。

每个图像是28像素乘以28像素。 我们可以把它解释为一大批数字：

我们可以把这个数组变成一个28×28 = 784数字的向量。从这个角度来看，MNIST图像只是一个784维向量空间中的一个点。这样我们就把mnist.train.images表示为一个形状为[55000,784]的张量（n维数组）。 第一个维度是图像列表中的索引，第二个维度是每个图像中每个像素的索引。 对于特定图像中的特定像素，张量中的每个条目是0和1之间的像素强度。

MNIST中的每个图像都具有相应的标签，0到9之间的数字表示图像中绘制的数字。我们将要将我们的标签称为“one-hot vectors”。 一个one-hot vectors是其他维数为0，单个维度为1的向量。 在这种情况下，第n个数字将被表示为在第n维中为1的向量。 例如，3将是[0,0,0,1,0,0,0,0,0,0]。 因此，mnist.train.labels是一个[55000,10]的浮点数组。

Softmax Regressions建模：
我们知道MNIST中的每个图像都是零到九之间的手写数字。所以给定的图像只有十个可能的东西可以。我们希望能够看到一个图像，并给出它作为每个数字的概率。例如，我们的模型可能会看到一个9的图片，并且有80％的人肯定它是一个9，但是给出5％的机会是8，并且有一点概率给所有其他人，因为它不是100％确定。这是一个经典的情况，其中softmax回归是一种自然，简单的模型。 如果要将概率分配给几个不同的东西之一的对象，softmax非常适合做这个事，因为softmax给出了一个0到1之间的值列表，加起来为1.即使在以后，当我们训练的模型更复杂，最后一步也是softmax层。

softmax回归有两个步骤：首先，我们将输入的evidence加在某些类中，然后将该evidence转换为概率。

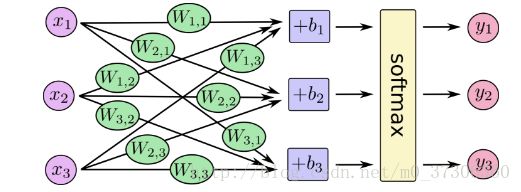
为了统计给定图像在特定类中的证据，我们进行像素强度的加权和。 如果像素是给该图是该类所起贡献是不利的证据，那么权重是负的，如果是有利的证据则为正。

我们还增加了一些称为偏置的额外证据。 基本上，我们希望能够说一些事情更有可能独立于输入。The result is that the evidence for a class i given an input x is:：

通过softmax转换为概率：

输入为指数化，最后进行归一化从而形成一个概率分布。

我们可以把像素看出x，对应的标签看成y，首先搭建神经网络：

写成等式形式：

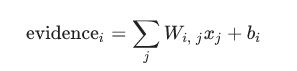
我们可以“矢量化”这个过程，把它变成矩阵乘法和向量加法：

更紧凑和简洁，我们可以写：

代码实现：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2017/7/10
# @Author  : yuquanle
# @Software: PyCharm

from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf

# 注册一个默认的Session，之后的运算都跑在这个session里面
sess = tf.InteractiveSession()
# 读取数据，one_hot是10类表示的师0-9的10个数字
mnist = input_data.read_data_sets("MNIST_data", one_hot = True)
# 创建一个Placeholder，输入数据的地方，参数（数据类型，tensor的shape），其中None表示不限制条数输入，n表示n维向量
x = tf.placeholder(tf.float32, [None, 784])
# 初始化weight和biases全部初始化为0，模型训练会选择合适的值
w = tf.Variable(tf.zeros([784, 10]))
# 其中w的shape是[784,10],784为特征数，10代表有10类，因为one_hot编码后是10维向量
b = tf.Variable(tf.zeros([10]))
# tf.nn包含大量的神经网络的组件，tf.matmul是矩阵乘法
y = tf.nn.softmax(tf.matmul(x, w) + b)
# 定义一个模型分类的损失函数，损失越小，模型越准确
y_ = tf.placeholder(tf.float32, [None, 10])
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1])) # 一个信息熵的计算
# 优化算法，随机梯度下降SGD，通过反向传播进行训练更新参数减少loss，学习速率0.5，优化目标就是定义的loss
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
# 使用全局参数初始化器tf.global_variables_initializer,运行其run方法
tf.global_variables_initializer().run()

for i in range(1000):
    # 每次随机从训练集中抽取100条样本构成一个mini_batch，并feed给placeholder
    batch_xs, batch_ys = mnist.train.next_batch(100)
    # 小样本避免全局样本的局部最优，以及速度问题，小样本收敛速度越快
    train_step.run({x: batch_xs, y_: batch_ys})

# 对于模型的准确性验证，tf,argmax寻找最大值的序号，tf.equal用于判断是否分类到正确类别
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
# 统计全部样本的精度，tf.cast将之前的correct_prediction输出的bool值转化为float32，再去求平均值
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
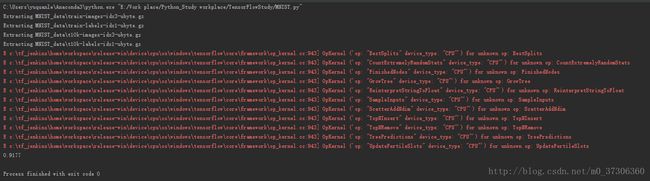
print(accuracy.eval({x:mnist.test.images, y_:mnist.test.labels}))

运行结果：