OpenCV--Python 图像平滑之高斯平滑、均值平滑

1.高斯平滑

（1）高斯卷积核的构建

假设构造宽（列数）为、高（行数）为的高斯卷积算子，其中和均为奇数，锚点的位置在，步骤如下：

第一步：计算高斯矩阵。

              

              其中        

              r，c代表位置索引，其中，，且r，c均为整数。

第二步：计算高斯矩阵的和。

             

第三步：高斯矩阵除以其本身的和，即归一化，得到的便是高斯卷积算子。

              

利用以上三个步骤构建高斯卷积算子的Python实现代码如下：

def getGaussKernel(sigma, H, W):
    # 第一步：构建高斯矩阵
    gaussMatrix = np.zeros([H, W], np.float32)
    # 得到中心点的位置
    cH = (H - 1) / 2
    cW = (W - 1) / 2
    # 计算gauss(sigma, r, c)
    for r in range(H):
        for c in range(W):
            norm2 = math.pow(r - cH, 2) + math.pow(c - cH, 2)
            gaussMatrix[r][c] = math.exp(-norm2 / (2 * math.pow(sigma, 2)))
    # 第二步：计算高斯矩阵的和
    sumGM = np.sum(gaussMatrix)
    # 第三步：归一化
    gaussKernel = gaussMatrix / sumGM
    return gaussKernel

因为最后要归一化，所以在代码实现中可以去掉高斯函数中的系数。高斯卷积算子翻转和本身是相同的。

高斯卷积算子是可分离卷积核，因为，所以高斯卷积核可分离成一维水平方向上的高斯核和一维垂直方向上的高斯核，或者反过来，即：

基于这种分离性，OpenCV只给出了构建一维垂直方向上的高斯卷积核的函数：

retval=cv.getGaussianKernel(ksize, sigma[, ktype])

参数	解释
ksize	一维垂直方向上高斯核的行数，而且是正奇数
sigma	标准差
ktype	返回值的数值类型为CV_32F或CV_64F，默认是CV_64F

返回值就是一个的垂直方向上的高斯核，而对于一维水平方向上的高斯核，只需对垂直方向上的高斯核进行转置就可以了。

import cv2 as cv
from scipy import signal
# 垂直方向上的卷积核
gk_y = cv.getGaussianKernel(5, 2, cv.CV_64F)
# 水平方向上的卷积核
gk_x = gk_y.T
print(gk_x)
print(gk_y)
# 高斯卷积核
gk = signal.convolve2d(gk_y, gk_x, mode="full")
print(gk)
'''
[[ 0.15246914  0.2218413   0.25137912  0.2218413   0.15246914]]
[[ 0.15246914]
 [ 0.2218413 ]
 [ 0.25137912]
 [ 0.2218413 ]
 [ 0.15246914]]
[[ 0.02324684  0.03382395  0.03832756  0.03382395  0.02324684]
 [ 0.03382395  0.04921356  0.05576627  0.04921356  0.03382395]
 [ 0.03832756  0.05576627  0.06319146  0.05576627  0.03832756]
 [ 0.03382395  0.04921356  0.05576627  0.04921356  0.03382395]
 [ 0.02324684  0.03382395  0.03832756  0.03382395  0.02324684]]
'''

（2）Python实现

def gaussBlur(img, sigma, H, W, _boundary='fill', _fillvalue=0):
    # 构建水平方向上的高斯卷积核
    gaussKernel_x = cv.getGaussianKernel(W, sigma, cv.CV_64F)
    # 转置
    gaussKernel_x = np.transpose(gaussKernel_x)
    # 图像矩阵与水平高斯核卷积
    gaussBlur_x = signal.convolve2d(img, gaussKernel_x, mode="same",
                                    boundary=_boundary, fillvalue=_fillvalue)
    # 构建垂直方向上的高斯卷积核
    gaussKernel_y = cv.getGaussianKernel(H, sigma, cv.CV_64F)
    # 与垂直方向上的高斯卷核
    gaussBlur_xy = signal.convolve2d(gaussBlur_x, gaussKernel_y, mode="same",
                                     boundary=_boundary, fillvalue=_fillvalue)
    return gaussBlur_xy

img = cv.imread("../testImages/5/img3.jpg", 0)
cv.imshow("img", img)
# 高斯平滑(使用自己的函数)
blurImg = gaussBlur(img, 2, 9, 9, "symm")
# 对blurImg进行灰度级显示
blurImg = np.round(blurImg)
blurImg = blurImg.astype(np.uint8)
# 高斯平滑(使用OpenCv提供的函数)
blurImg2 = cv.GaussianBlur(img, (9, 9), 2)
cv.imshow("blur", blurImg)
cv.imshow("blur2", blurImg2)
cv.waitKey()

上述示例使用了OpenCV提供的高斯平滑函数，下面来看看OpenCV提供的高斯平滑函数：

dst=cv.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]])

参数	解释
src	输入矩阵
dst	输出矩阵，大小和数据类型与src相同
ksize	高斯卷积核的大小，宽、高均为奇数，且可以不同
sigmaX	一维水平方向高斯卷积核的标准差
sigmaY	一维垂直方向高斯卷积核的标准差，默认值为0，表示与sigmaX相同
borderType	边界扩充方式

从参数的设置可以看出，GaussianBlur也是通过分离的高斯卷积核实现的，也可以令水平方向和垂直方向上的标准差不同，但是一般会取相同的标准差。当平滑窗口比较小时，对标准差的变化不是很敏感，得到的高斯平滑效果差别不大；相反，当平滑窗口较大时，对标准差的变化很敏感，得到的高斯平滑效果差别较大。

下图显示了使用不同尺寸标准差的高斯核对图（a）进行高斯平滑的结果，随着卷积核尺寸和标准差的增大，平滑效果越来越明显，图像变得越来越模糊，只能显示大概的轮廓。

（a）原图                             （b）9x9,sigma=2                           （c）11x11,sigma=3                             （d）25x25,sigma=9

2.均值平滑

（1）均值卷积核的构建

高为、宽为的均值卷积算子的构建方法很简单，令所有元素均为即可，记：

                                                   

其中、均为奇数，锚点的位置在。

均值平滑算子是可分离卷积核，即：

均值平滑，图像中每一个位置的邻域的平均值作为该位置的输出值，代码实现与分离的高斯卷积是类似的，只需将高斯算子替换成均值算子即可。利用卷积核的分离性和卷积的结合律，虽然减少了运算量，但是随着卷积核窗口的增加，计算量仍会继续增大，可以利用图像的积分，实现时间复杂度为的快速均值平滑。

（2）快速均值平滑

先来介绍一下图像的积分，行列的图像矩阵的积分由以下定义计算：

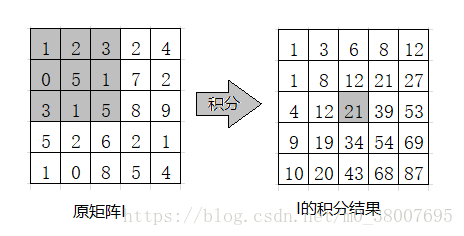
即任意一个位置的积分等于该位置左上角所有值的和。举例如下图：

利用矩阵的积分可以计算出矩阵中任意矩形区域的和：

                    

                                          

举例：计算的以为中心，从左上角至右下角的矩形区域的和：

可以从积分后的图像矩阵中找到对应的值计算：

                 

           即：

       均值平滑的原理本质上是计算任意一个点的邻域的平均值，而平均值是由该邻域的和除以邻域的面积得到的。这样无论怎样改变平滑窗口的大小，都可以利用图像的积分快速计算每个邻域的和。接下来利用图像的积分实现图像的均值平滑。

（3）Python实现

       对于图像的积分的实现，可以分两步完成：先对图像矩阵按行积分，然后在按列积分；或者反过来，先列积分后行积分。为了在快速均值平滑中省去判断边界的问题，所以对积分后图像矩阵的上边和左边进行补零操作，尺寸为，代码如下：

def integral(img):
    rows, cols = img.shape
    # 行积分运算
    inteImageC = np.zeros(img.shape, np.float32)
    for r in range(rows):
        for c in range(cols):
            if c == 0:
                inteImageC[r][c] = img[r][c]
            else:
                inteImageC[r][c] = inteImageC[r][c - 1] + img[r][c]
    # 列积分计算
    inteImage = np.zeros(img.shape, np.float32)
    for c in range(cols):
        for r in range(rows):
            if r == 0:
                inteImage[r][c] = inteImageC[r][c]
            else:
                inteImage[r][c] = inteImage[r - 1][c] + inteImageC[r][c]
    # 上边和左边进行补零
    inteImage_0 = np.zeros((rows + 1, cols + 1), np.float32)
    inteImage_0[1:rows + 1, 1:cols + 1] = inteImage
    return inteImage_0

实现了图像的积分后，来实现均值平滑，如果在图像的边界进行的是补零操作，那么随着窗口的增大，平滑后黑色边界会越来越明显， 所以在进行均值平滑处理时，比较理想的边界扩充类型是镜像扩充。代码如下：

def fastMeanBlur(img, winSize, borderType=cv.BORDER_DEFAULT):
    halfH = int((winSize[0] - 1) / 2)
    halfW = int((winSize[1] - 1) / 2)
    ratio = 1.0 / (winSize[0] * winSize[1])
    # 边界扩充
    paddImage = cv.copyMakeBorder(img, halfH, halfH, halfW, halfW, borderType)
    # 图像积分
    paddIntegral = integral(paddImage)
    # 图像的高、宽
    rows, cols = img.shape
    # 均值滤波后的结果
    meanBlurImage = np.zeros(img.shape, np.float32)
    r, c = 0, 0
    for h in range(halfH, halfH + rows, 1):
        for w in range(halfW, halfW + cols, 1):
            meanBlurImage[r][c] = (paddIntegral[h + halfH + 1][w + halfW + 1] +
                                   paddIntegral[h - halfH][w - halfW] -
                                   paddIntegral[h + halfH + 1][w - halfW] -
                                   paddIntegral[h - halfH][w + halfW + 1]) * ratio
            c += 1
        r += 1
        c = 0
    return meanBlurImage
img = cv.imread("../testImages/5/img2.png", 0)
cv.imshow("img", img)
# 使用自己的函数
blur = fastMeanBlur(img, (5, 5))
blur = np.round(blur)
blur = blur.astype(np.uint8)
# # 使用OpenCV提供的函数
# blur2 = cv.blur(img, (5, 5))
cv.imshow("blur", blur)
# cv.imshow("blur2", blur2)
cv.waitKey()

函数fastMeanBlur返回的结果是浮点型，如果输入的是8位图，则需要使用astype(numpu.uint8)将结果转换为8位图。下图显示的是不同尺寸的均值平滑算子对图（a）平滑的效果，显然随着均值平滑算子窗口的增大，处理细节部分越来越不明显，只是显示了大概轮廓。

（a）原图                          （b）5x5均值平滑                       （c）7x7均值平滑                     （d）11x11均值平滑

       对于快速均值平滑，OpenCV提供了boxFilter和blur两个函数来实现该功能，而且这两个函数均可以处理多通道图像矩阵，本质上是对图像的每一个通道分别进行均值平滑。

dst = cv.boxFilter(src, ddepth, ksize[, dst[, anchor[, normalize[, borderType]]]])

参数	解释
src	输入矩阵
dst	输出矩阵，其大小和数据类型与src相同
ddepth	位深
ksize	平滑窗口的尺寸
normalize	是否归一化

dst=cv.blur(src, ksize[, dst[, anchor[, borderType]]])

参数	解释
src	输入矩阵
dst	输出矩阵，其大小和数据类型与src相同
ksize	均值算子的尺寸，Size（宽，高）
anchor	锚点，如果高、宽为奇数，则Point(-1,-1)表示中心点
borderType	边界扩充方式

显然，函数  boxFilter(src, src.dtype(), ksize, anchor=Point(-1,-1), normalize=True, borderType=cv.BORDER_DEFAULT)  与函数blur的作用是一样的。示例如下：

img = cv.imread("../testImages/5/img2.png", 0)
cv.imshow("img", img)
# 使用OpenCV提供的函数
blur2 = cv.blur(img, (5, 5))
cv.imshow("blur2", blur2)
cv.waitKey()

 

这篇文章主要了解了高斯平滑和均值平滑的原理以及他们各自使用的函数，都是基于卷积运算的图像平滑算法。