《DeepLab v1:semantic image segmentation with deep convolutional nets and fully connected CRFs》论文笔记
1. 概述
导读:文章指出仅仅使用DCNNs网络的最后一层实现精确地语义分割是不足够的。为此,本篇文章的工作将DCNNs与概率图模型来共同解决分割精度的问题。文章新提出的这个方法在定位分割的边界上超过了之前的方法(当时),在VOC 2012数据集上取得了71.6%的IOU,GPU上速度为8 FPS(不含CRF)。
相比于传统的视觉算法(SIFT或HOG),DCNNs以其end-to-end方式获得了很好的效果。这样的成功部分可以归功于DCNN对图像转换的平移不变性(invariance),这根本是源于重复的池化和下采样组合层。平移不变性增强了对数据分层抽象的能力,但同时可能会阻碍低级(low-level)视觉任务,例如姿态估计、语义分割等,在这些任务中我们倾向于精确的定位而不是抽象的空间关系。
DCNN在图像标记任务中存在两个技术障碍:
- 1)信号下采样,这是由于CNN网络中的池化操作以及下采样带来的分辨率下降问题,这个过程中会丢失掉很多细节信息,DeepLab v1中使用Atrous卷积增大感受野,获取尽可能多的上下文信息;
- 2)空间不敏感(invariance),分类器获取以对象中心的决策是需要空间变换的不变性,这天然的限制了DCNN的定位精度,DeepLab采用完全连接的条件随机场(DenseCRF)提高模型捕获细节的能力。
这篇文章提出的新方法Deeplab v1具有如下的特点:
- 1)快速,由于孔洞卷积的好处使得模型的帧率为8FPS,然而使用Mean Field方法inference全连接CRF需要0.5s;
- 2)精度,文章提出的新方法在VOC数据集上的性能超过第二名7.2%;
- 3)网络简洁,文中的方法将DCNNs与CRF结合去获得最后的分割结果;
2. 网路设计
2.1 CNN网络部分设计
这里使用的是VGG16作为基础网络,并且将其中的全连接层替换为了卷积层,在图像的原始分辨率上产生非常稀疏的计算检测分数(stride=32),为了以更密集(步幅8)的计算得分,我们在最后的两个最大池化层不下采样(padding到原大小),再通过2或4的采样率的空洞卷积对特征图做采样扩大感受野,缩小步幅。下面这幅图是在以为上使用Atrous方法的运算流程:
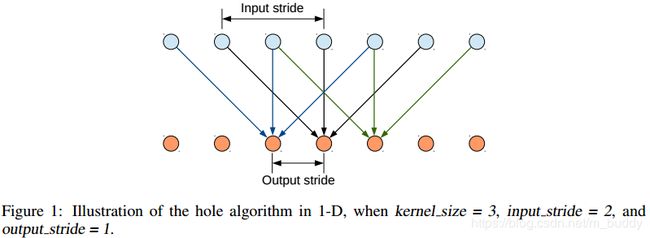
这种带孔的采样又称Atrous算法,可以稀疏的采样底层特征映射,该方法具有通常性,并且可以使用任何采样率计算密集的特征映射。在VGG16中使用不同采样率的空洞卷积,可以让模型再密集的计算时,明确控制网络的感受野。保证DCNN的预测图可靠的预测图像中物体的位置。
训练时将预训练的VGG16的权重做fine-tune,损失函数取是输出的特征图与ground truth下采样8倍做交叉熵和;测试时取输出图双线性上采样8倍得到结果。但DCNN的预测物体的位置是粗略的,没有确切的轮廓。在卷积网络中,因为有多个最大池化层和下采样的重复组合层使得模型的具有平移不变性,我们在其输出的high-level的基础上做定位是比较难的。这需要做分类精度和定位精度之间是有一个自然的折中。
解决这个问题的工作,主要分为两个方向:
- 1)第一种是利用卷积网络中多个层次的信息
- 2)第二种是采样超像素表示,实质上是将定位任务交给低级的分割方法
DeepLab v1是结合了DCNNs的识别能力和全连接的CRF的细粒度定位精度,寻求一个结合的方法,结果证明能够产生准确的语义分割结果。
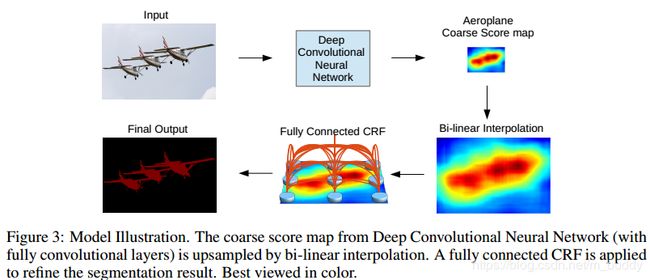
2.2 CRF运用于语义分割

上图展示了CRF使用在语义分割上面的结果,随着迭代的进行分割的效果更佳精细。
对于每个像素位置 i i i具有隐变量 x i x_i xi(这里隐变量就是像素的真实类别标签,如果预测结果有21类,则( i ∈ 1 , 2 , … , 21 ) i\in 1,2,\dots,21) i∈1,2,…,21)),还有对应的观测值 y i y_i yi(即像素点对应的颜色值)。以像素为节点,像素与像素间的关系作为边,构成了一个条件随机场(CRF)。通过观测变量 y i y_i yi来推测像素位置 i i i对应的类别标签 x i x_i xi。条件随机场示意图如下
条件随机场符合吉布斯分布( x x x是上面的观测值,下面省略全局观测 I I I):
P ( x ∣ I ) = 1 Z e x p ( − E ( x ∣ I ) ) P(x|I)=\frac{1}{Z}exp(-E(x|I)) P(x∣I)=Z1exp(−E(x∣I))
全连接的CRF模型使用的能量函数 E ( x ) E(x) E(x)为:
E ( x ) = ∑ i θ i ( x i ) + ∑ i j θ i j ( x i , x j ) E(x)=\sum_i \theta_i(x_i)+\sum_{ij}\theta_{ij}(x_i,x_j) E(x)=i∑θi(xi)+ij∑θij(xi,xj)
这分为一元势函数 θ i ( x i ) \theta_i(x_i) θi(xi)和二元势函数 θ i j ( x i , x j ) \theta_{ij}(x_i,x_j) θij(xi,xj)两部分。
一元势函数是定义在观测序列位置 i i i的状态特征函数,用于刻画观测序列对标记变量的影响。在这里定义为:
θ i ( x i ) = − l o g P ( x i ) \theta_i(x_i)=-logP(x_i) θi(xi)=−logP(xi)
说白了,就是观测到的像素点 i i i的当前像素为 y i y_i yi,则其对应的标签 x i x_i xi的概率值(例如城市道路任务中,观测到的像素点为黑色,对应的车子可能比天空可能性大)。以前这个一元势函数通过分类器完成,现在DeepLab中有了DCNN来做像素分割,所以这里 P ( x i ) P(x_i) P(xi)是取DCNN计算关于像素 i i i的输出的标签分类概率。
二元势函数是定义在不同观测位置上的转移特征函数,用于 **刻画变量之间的相关关系以及观测序列对其影响。**这里定义为:
θ i j ( x i , x j ) = u ( x i , x j ) ∑ m = 1 K w m k m ( f i , f j ) \theta_{ij}(x_i,x_j)=u(x_i,x_j)\sum_{m=1}^{K}w_mk^m(f_i,f_j) θij(xi,xj)=u(xi,xj)m=1∑Kwmkm(fi,fj)
其中:
- u ( x i , x j ) = 1 , i f x i ≠ y i ; u ( x i , x j ) = 0 , i f x i = y i ; u(x_i,x_j)=1,if x_i \neq y_i;u(x_i,x_j)=0,if x_i=y_i; u(xi,xj)=1,ifxi̸=yi;u(xi,xj)=0,ifxi=yi;,因为是全连接,所以每个像素对都会有值;
- k m ( f i , f j ) k^m(f_i,f_j) km(fi,fj)是 ( f i , f j ) (f_i,f_j) (fi,fj)之间的高斯核, f i f_i fi是像素 i i i的特征向量,例如像素点 i i i的特征向量 f i f_i fi用 ( x , y , r , g , b ) (x,y,r,g,b) (x,y,r,g,b)表示。
- 对应的权重为 w m w_m wm。
在DeepLab中高斯核采用双边位置和颜色组合,定义为:
θ i j ( x i , x j ) = [ w 1 e x p ( − ∣ ∣ p i − p j ∣ ∣ 2 2 σ α 2 − ∣ ∣ I i − I j ∣ ∣ 2 2 σ β 2 ) + w 2 e x p ( − ∣ ∣ p i − p j ∣ ∣ 2 2 σ γ 2 ) ] \theta_{ij}(x_i,x_j)=[w_1exp(-\frac{||p_i-p_j||^2}{2\sigma_{\alpha}^2}-\frac{||I_i-I_j||^2}{2\sigma_{\beta}^2})+w_2exp(-\frac{||p_i-p_j||^2}{2\sigma_{\gamma}^2})] θij(xi,xj)=[w1exp(−2σα2∣∣pi−pj∣∣2−2σβ2∣∣Ii−Ij∣∣2)+w2exp(−2σγ2∣∣pi−pj∣∣2)]
第一核取决于像素位置( p p p)和像素颜色强度( I I I),第二个核取决于像素位置( p p p).
说白了,二元势函数是描述像素和像素之间的关系,如果比较相似,那可能是一类,否则就裂开,这可以细化边缘。一般的二元势函数只取像素点与周围像素之间的边,这里使用的是全连接,即像素点与其他所有像素之间的关系。
这个公式看起来是很麻烦的,实际上计算时分解近似的平均场然后再计算,感兴趣可参考对应论文。
2.3 多尺度预测
论文还探讨了使用多尺度预测提高边界定位效果。具体的,在输入图像和前四个最大池化层的输出上附加了两层的MLP(第一层是128个3×3卷积,第二层是128个1×1卷积),最终输出的特征映射送到模型的最后一层辅助预测,合起来模型最后的softmax层输入特征多了5×128=640个通道,实验表示多尺度有助于提升预测结果,但是效果不如CRF明显(CRF提升4%,这部分只提升了1.5%)。
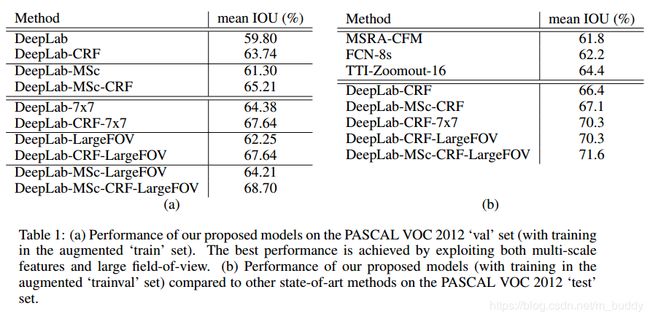
3 实验结果
4. 参考
- Semantic Segmentation – (DeepLabv1)Semantic image segmentation with deep convolutional … CRFs论文解读