算法篇--------排序算法
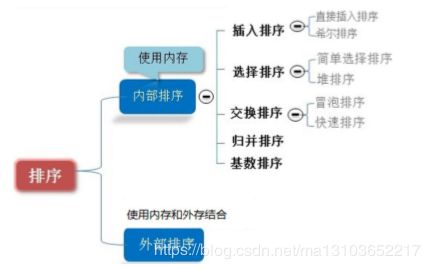
常见的排序算法分类(持续更新中…)
冒泡排序
基本思想:
冒泡排序主要思想是:通过对待排序序列从前向后(从下标较小的元素开始),依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就像水底下的气泡一样逐渐向上冒
算法优化:
不管是否有序,都要进行n-1趟循环如何判断有序:比较了一趟,没有发生交换
(解决:定义一个符号量flag,默认有序true;发生交换,置为false,
一趟循环结束后,根据flag的值判断是否有序;有序,退出即可)

/**
* 冒泡排序
* @-马先森
*
*/
public class TestBubbleSort2{
public static void main(String [] args){
//定义一个无序数组
//int [] scoreArr = {75,87,56,45,89,100,76,34,89,97};
int [] scoreArr = {1,2,3,4,5,6,7};
//排序前输出
System.out.println("排序前");
for(int score :scoreArr){
System.out.print(score+"\t");
}
//排序
//大循环:n个元素排序,则至多需要n-1趟循环
int temp;
int i;
for(i=0;i scoreArr[j+1]){
//交换
temp = scoreArr[j];
scoreArr[j] = scoreArr[j+1];
scoreArr[j+1] = temp;
//发生了交换,数组无序
flag = false;
}
}
//3.判断是否有序,有序,退出
if(flag){
break;
}
}
//排序后输出
System.out.println("排序后");
for(int score :scoreArr){
System.out.print(score+"\t");
}
System.out.println("\n一共进行了"+(i+1)+"趟循环");
}
}
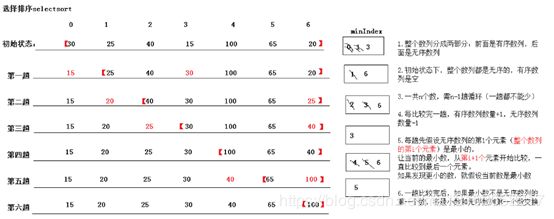
选择排序算法
基本思想
* 1.整个数列分成两部分:前面是有序数列,后面是无序数列
* 2.初始状态下,整个数列都是无序的,有序数列是空
* 3.一共n个数,需要n-1趟循环(一趟都不能少)
* 4.每比较完一趟,有序数列数量+1,无序数列数量-1
* 5.每趟先假设无序数列的第1个元素(整个数列的第i个元素)是最小的,
让当前的最小数,从第i+1个元素开始比较,一直比较到最后一个元素。
如果发现更小的数,就假设当前数是最小数。
* 6.一趟比较完后,将发现最小数和无序数列的第一个数交换(如果最小数不是无序数列的第一个数)
/**
* 选择排序
* @-马先森
*
*/
public static void main(String[] args) {
18. //给定无序的数组
19. int [] scoreArr = {75,87,56,45,89,100,76,34,89,97};
20. //输出无序的数组
21. System.out.println(Arrays.toString(scoreArr));
22.
23. //选择排序
24. selectSort(scoreArr);
25. //输出有序的数组
26. System.out.println(Arrays.toString(scoreArr));
27. }
28.
29. public static void selectSort(int[] scoreArr) {
30. //大循环:n个元素排序,则需要n-1趟循环
31. for(int i=0;i scoreArr[j]){
37. minIndex = j;
38. }
39. }
40. //一趟比较完后,或者最小值的索引,如果不是第i个,就交换
41. if(minIndex !=i){
42. int temp;
43. temp = scoreArr[i];
44. scoreArr[i] = scoreArr[minIndex];
45. scoreArr[minIndex] = temp;
46. }
47. }
48. }
49. }
插入排序
package ch02;
/**
* 插入排序
* @-马先森
*
*/
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class InsertSort {
public static void main(String[] args) {
//int[] arr = {101, 34, 119, 1, -1, 89};
// 创建要给80000个的随机的数组
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
System.out.println("插入排序前");
Date data1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(data1);
System.out.println("排序前的时间是=" + date1Str);
insertSort(arr); //调用插入排序算法
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
//System.out.println(Arrays.toString(arr));
}
//插入排序
public static void insertSort(int[] arr) {
int insertVal = 0;
int insertIndex = 0;
//使用for循环来把代码简化
for(int i = 1; i < arr.length; i++) {
//定义待插入的数
insertVal = arr[i];
insertIndex = i - 1; // 即arr[1]的前面这个数的下标
// 给insertVal 找到插入的位置
// 说明
// 1. insertIndex >= 0 保证在给insertVal 找插入位置,不越界
// 2. insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置
// 3. 就需要将 arr[insertIndex] 后移
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
// 当退出while循环时,说明插入的位置找到, insertIndex + 1
// 举例:理解不了,我们一会 debug
//这里我们判断是否需要赋值
if(insertIndex + 1 != i) {
arr[insertIndex + 1] = insertVal;
}
//System.out.println("第"+i+"轮插入");
//System.out.println(Arrays.toString(arr));
}
/*
//使用逐步推导的方式来讲解,便利理解
//第1轮 {101, 34, 119, 1}; => {34, 101, 119, 1}
//{101, 34, 119, 1}; => {101,101,119,1}
//定义待插入的数
int insertVal = arr[1];
int insertIndex = 1 - 1; //即arr[1]的前面这个数的下标
//给insertVal 找到插入的位置
//说明
//1. insertIndex >= 0 保证在给insertVal 找插入位置,不越界
//2. insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置
//3. 就需要将 arr[insertIndex] 后移
while(insertIndex >= 0 && insertVal < arr[insertIndex] ) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
//当退出while循环时,说明插入的位置找到, insertIndex + 1
//举例:理解不了,我们一会 debug
arr[insertIndex + 1] = insertVal;
System.out.println("第1轮插入");
System.out.println(Arrays.toString(arr));
//第2轮
insertVal = arr[2];
insertIndex = 2 - 1;
while(insertIndex >= 0 && insertVal < arr[insertIndex] ) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
arr[insertIndex + 1] = insertVal;
System.out.println("第2轮插入");
System.out.println(Arrays.toString(arr));
//第3轮
insertVal = arr[3];
insertIndex = 3 - 1;
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
arr[insertIndex + 1] = insertVal;
System.out.println("第3轮插入");
System.out.println(Arrays.toString(arr)); */
}
}
快速排序
基本思想
首先在数组中选择一个基准点(该基准点的选取可能影响快速排序的效率,后面讲解选取的方法),然后分别从数组的两端扫描数组,设两个指示标志(low指向起始位置,high指向末尾),首先从后半部分开始,如果发现有元素比该基准点的值小,就交换low和high位置的值,然后从前半部分开始扫秒,发现有元素大于基准点的值,就交换low和high位置的值,如此往复循环,直到low>=high,然后把基准点的值放到high这个位置。一次排序就完成了。以后采用递归的方式分别对前半部分和后半部分排序,当前半部分和后半部分均有序时该数组就自然有序了。
package com.xiaoma.maxiaotian;
import java.util.Arrays;
/**
*快速排序
*@-马先森
*/
public class QuickSort {
public static void main(String[] args) {
final int MAX = 15;
int[] nums = new int[MAX];
System.out.println("...............使用的是选择排序算法...............");
for (int i = 0; i < MAX; i++) {
nums[i] = (int) (Math.random() * 10 + 5);
}
System.out.println("排序之前的数组为...............");
System.out.println(Arrays.toString(nums));
System.out.println("排序之后的数组为...............");
//使用选择排序算法进行排序:
QuickSort sort = new QuickSort();
sort.quickSort(nums, 0, nums.length - 1);
System.out.println(Arrays.toString(nums));
}
public void quickSort(int[] nums, int low, int high) {
if (low < high) {
int middle = getMiddle(nums, low, high);
//对左子序列进行排序
quickSort(nums, low, middle - 1);
//对右子序列进行排序
quickSort(nums, middle + 1, high);
}
}
private int getMiddle(int[] nums, int low, int high) {
//当前数组的第一个元素作为中轴(基准)
int temp = nums[low];
while (low < high) {
//这里temp <= nums[high]中等号的情况相当于数组中出现了两个相等的数字,循环比较依然能够继续
while (low < high && temp <= nums[high]) {
high--;
}
nums[low] = nums[high];
while (low < high && temp >= nums[low]) {
low++;
}
nums[high] = nums[low];
}
nums[low] = temp;
return low;
}
}
归并排序
基本思想
归并排序的核心思想是将两个有序的数列合并成一个大的有序的序列。通过递归,层层合并,即为归并。


package com.xiaoma.sort;
/**
*归并排序
*@-马先森
*/
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class MergetSort {
public static void main(String[] args) {
//int arr[] = { 8, 4, 5, 7, 1, 3, 6, 2 }; //
//测试快排的执行速度
// 创建要给80000个的随机的数组
int[] arr = new int[8000000];
for (int i = 0; i < 8000000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
System.out.println("排序前");
Date data1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(data1);
System.out.println("排序前的时间是=" + date1Str);
int temp[] = new int[arr.length]; //归并排序需要一个额外空间
mergeSort(arr, 0, arr.length - 1, temp);
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
//System.out.println("归并排序后=" + Arrays.toString(arr));
}
//分+合方法
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if(left < right) {
int mid = (left + right) / 2; //中间索引
//向左递归进行分解
mergeSort(arr, left, mid, temp);
//向右递归进行分解
mergeSort(arr, mid + 1, right, temp);
//合并
merge(arr, left, mid, right, temp);
}
}
//合并的方法
/**
*
* @param arr 排序的原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
* @param temp 做中转的数组
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left; // 初始化i, 左边有序序列的初始索引
int j = mid + 1; //初始化j, 右边有序序列的初始索引
int t = 0; // 指向temp数组的当前索引
//(一)
//先把左右两边(有序)的数据按照规则填充到temp数组
//直到左右两边的有序序列,有一边处理完毕为止
while (i <= mid && j <= right) {//继续
//如果左边的有序序列的当前元素,小于等于右边有序序列的当前元素
//即将左边的当前元素,填充到 temp数组
//然后 t++, i++
if(arr[i] <= arr[j]) {
temp[t] = arr[i];
t += 1;
i += 1;
} else { //反之,将右边有序序列的当前元素,填充到temp数组
temp[t] = arr[j];
t += 1;
j += 1;
}
}
//(二)
//把有剩余数据的一边的数据依次全部填充到temp
while( i <= mid) { //左边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[i];
t += 1;
i += 1;
}
while( j <= right) { //右边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[j];
t += 1;
j += 1;
}
//(三)
//将temp数组的元素拷贝到arr
//注意,并不是每次都拷贝所有
t = 0;
int tempLeft = left; //
//第一次合并 tempLeft = 0 , right = 1 // tempLeft = 2 right = 3 // tL=0 ri=3
//最后一次 tempLeft = 0 right = 7
while(tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
}