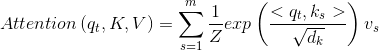文献阅读笔记—Attention is ALL You Need

本文主要是参考

https://yq.aliyun.com/articles/342508?utm_content=m_39938

https://mchromiak.github.io/articles/2017/Sep/12/Transformer-Attention-is-all-you-need/#positional-encoding-pe

将互相缺少的融合到一起，略微加了点其他东西。

一、简介

对于Seq2Seq任务，均采用encoder-decoder+attention的模型，以往的encoder-decoder采用rnn或cnn，捕捉输入输出的全局信息，attention捕捉输入和输出之间的侧重关系；而这篇google大作，采用的是attention做encoder-decoder；也就是说，模型中只有attention， 没有rnn或者cnn。

二、模型整体架构

encoder由6个相同的层堆叠在一起，每一层又有两个支层。第一个支层是一个多头的自注意机制（Multi-head attention），第二个支层是一个简单的全连接前馈网络（position-wise FFN）。在两个支层外面都添加了一个residual的连接，然后进行了layer nomalization的操作。模型所有的支层以及embedding层的输出维度都是dmodel=512.

    Stage1_out = Embedding512 + TokenPositionEncoding512
    Stage2_out = layer_normalization(multihead_attention(Stage1_out) + Stage1_out)
    Stage3_out = layer_normalization(FFN(Stage2_out) + Stage2_out)
    out_enc = Stage3_out

decoder也是由6个相同的层堆叠在一起，不过每层除了编码器中那两个支层，还加入了第三个支层，即该层decoder和对应层encoder之间的多头注意力机制，同样也用了residual以及layer normalization，因为decoder时只能用这个token之前的tokens，那么做attention的时候需要添加一个mask将这个token及其之后的遮盖住（是一种从左到右预测的味道）。

    Stage1_out = OutputEmbedding512 + TokenPositionEncoding512
    Stage2_Mask = masked_multihead_attention(Stage1_out)
    Stage2_Norm1 = layer_normalization(Stage2_Mask + Stage1_out)
    Stage2_Multi = multihead_attention(Stage2_Norm1 + out_enc) +  Stage2_Norm1
    Stage2_Norm2 = layer_normalization(Stage2_Multi) + Stage2_Multi
    Stage3_FNN = FNN(Stage2_Norm2)
    Stage3_Norm = layer_normalization(Stage3_FNN + Stage2_Norm2) 
    out_dec = Stage3_Norm

三、分块解析

1. Scaled Dot-Product Attention

                   

                   

如果忽略激活函数 softmax 的话，那么事实上它就是三个  的矩阵相乘，最后的结果就是一个的矩阵。于是我们可以认为：这是一个 Attention 层，将的序列 Q 编码成了一个新的  的序列。

那怎么理解这种结构呢？我们不妨逐个向量来看。

                  

其中 Z 是归一化因子。事实上分别是 query,key,value 的简写， 是一一对应的，它们就像是 key-value 的关系，那么上式的意思就是通过  这个 query，通过与各个  内积的并 softmax 的方式，来得到  与各个  的相似度，然后加权求和，得到一个  维的向量。其中因子起到调节作用，使得内积不至于太大（太大的话 softmax 后就非 0 即 1 了，不够“soft”了），因为文章假设数据符合标准正态分布，为了使点乘结果的方差为1，所以使用了根号。

2. Multi-Head Attention

不过从形式上看，它其实就再简单不过了，就是把 通过参数矩阵映射一下，然后再做 Attention，把这个过程重复做 h 次，结果拼接起来就行了，可谓“大道至简”了。具体来说：

                    

                   

最后得到一个  的序列。所谓“多头”（Multi-Head），就是只多做几次同样的事情（参数不共享），然后把结果拼接。有点类似于cnn里面的多kernel。

本文中，大部分的 Attention 都是 Self Attention，即“自注意力”，或者叫内部注意力，就是， 就是前面说的输入序列。也就是说，在序列内部做 Attention，寻找序列内部的联系。decoder里面和encoder的attention是

3. position-wise FFN

一个position对应一个词，一个词对应矩阵的一行，该函数为对矩阵的每一行做两个线性映射，中间加一个ReLU，每一行的线性映射参数一样，相当于size为1的kernel。不同layer的两个线性映射参数不一致。记输入矩阵的某行为，则：

                   

4. position encoding

但是这样的模型并不能捕捉序列的顺序。换句话说，如果将  按行打乱顺序（相当于句子中的词序打乱），那么 Attention 的结果还是一样的。所以，到目前为止，Attention 模型顶多是一个非常精妙的“词袋模型”而已。 

但是对于时间序列来说，尤其是对于 NLP 中的任务来说，顺序是很重要的信息，它代表着局部甚至是全局的结构，学习不到顺序信息，那么效果将会大打折扣（比如机器翻译中，有可能只把每个词都翻译出来了，但是不能组织成合理的句子）。 

于是 引入——Position Embedding，也就是“位置向量”，将每个位置编号，然后每个编号对应一个向量，通过结合位置向量和词向量，就给每个词都引入了一定的位置信息，这样 Attention 就可以分辨出不同位置的词了。 

以前在 RNN、CNN 模型中其实都出现过 Position Embedding，但在那些模型中，Position Embedding 是锦上添花的辅助手段，也就是“有它会更好、没它也就差一点点”的情况，因为 RNN、CNN 本身就能捕捉到位置信息。但是在这个纯 Attention 模型中，Position Embedding 是位置信息的唯一来源，因此它是模型的核心成分之一。 

在以往的 Position Embedding 中，基本都是根据任务训练出来的向量。而 Google 直接给出了一个构造 Position Embedding 的公式：

                  

这里的意思是将位置  映射为一个 dpos 维的位置向量，这个向量的第 i 维的数值就是 PEi(p)。

Position Embedding 本身是一个绝对位置的信息，但在语言中，相对位置也很重要，由于我们有  以及 ，这表明位置  的向量可以表明位置  的向量的线性变换，这提供了表达相对位置信息的可能性。

结合位置向量和词向量有几个可选方案，可以把它们拼接起来作为一个新向量，也可以把位置向量定义为跟词向量一样大小，然后两者加起来，本文选择加起来。

四、优点

从三个方面去对比self-attention和递归结构、卷积结构的优劣性，首先是每一层的计算复杂度，其次是能够被并行的计算量，最后是网络中长期依赖的路径长度。对比显示，self-attention表现最好。

Attention 层的好处是能够一步到位捕捉到全局的联系，因为它直接把序列两两比较（代价是计算量变为 ，当然由于是纯矩阵运算，这个计算量相当也不是很严重）。相比之下，RNN 需要一步步递推才能捕捉到，而 CNN 则需要通过层叠来扩大感受野，这是 Attention 层的明显优势。