《Recent Advances in Convolutional Neural Networks》(一)

摘要——在过去的一些年里，深度学习在许多类问题上都取得了很好的表现，例如视觉识别，语音识别和自然语言处理。在众多不同类型的深度神经网络中，CNN是被最深入研究的网络。早些年，因为缺少训练数据和电脑计算能力较差，很难在不过拟合的情况下训练一个高性能的CNN。在注释数据大量增长和GPUs快速发展的今天，涌现了许多关于CNN的研究，并在众多任务中取得了state-of-the-art的结果。本文，我们将提供一个广泛的关于CNN最新进展的调查结果。
关键词——CNN，深度学习

I．引言

CNN是一种常见的深度学习架构，受生物的自然视觉感知机制启发而来。在1959年，Hubel & Wiesel 发现，动物视觉皮层细胞负责检测光学信号。受此启发，在1980年，Kunihiko Fukushima提出了CNN的前身——neocognitron。在1990年，LeCun等人发表了一篇有重大影响力的文章，确立了CNN的现代结构，并在稍后的工作中对其进行了改进。他们提出了一种名为LeNet-5的多层人工神经网络，该网络可以分类手写的数字。和其他的神经网络一样，LeNet-5拥有许多层，且可以通过后向backpropagation算法进行训练。CNN能够得出原始图像的有效表征，这使得CNN能够直接从原始像素中，经过极少的预处理，识别视觉上面的规律。然而，由于当时缺乏大规模训练数据，计算机的计算能力也跟不上，LeNet-5 对于复杂问题的处理结果并不理想。

2006年起，人们设计了很多方法，想要克服难以训练深度CNN的困难。其中，最著名的是 Krizhevsky等人提出了一个经典的CNN 结构，并在图像识别任务上取得了重大突破。其方法的整体框架叫做AlexNet，与LeNet-5类似，但要更加深一些。AlexNet取得成功后，研究人员又提出了其他的完善方法，其中最著名的要数ZFNet,VGGNet,GoogleNet和ResNet这四种。从结构看，CNN 发展的一个方向就是层数变得更多，LSVRC 2015冠军ResNet是AlexNet的20多倍，是VGGNet的8倍多。通过增加深度，网络便能够利用增加的非线性得出目标函数的近似结构，同时得出更好的特性表征。但是，这样做同时也增加了网络的整体复杂程度，使网络变得难以优化，很容易过拟合。研究员提出了很多方法来解决这一问题。本文，我们将试着对最近的进展给一个全面的回顾且进行一些详细的讨论。

在下面的章节中，我们会介绍一些与CNN相关的研究工作。我们在第二节会先列出CNN的组成部分，然后在第三节介绍CNN不同方面的最近进展，包括卷积层、pooling层、激活函数、损失函数、正则化和优化。接着在第四节引入快速计算技巧，并在第五节探讨CNN在图像分类、物体检测、物体跟踪、姿态估计、文本检测和识别、视觉显著性检测、运动识别和场景标记物体识别等不同方面的典型应用。最后，在第六节归纳总结。

II．CNN基础组成部分

文献里有众多不同的CNN架构。然而，他们的基本组成结构都非常相似。以著名的LeNet-5为例（见图1），它由三种类型的层组成，分别为卷积、pooling和全连接层。

图1：LeNet-5网络的架构，适用于手写数字分类

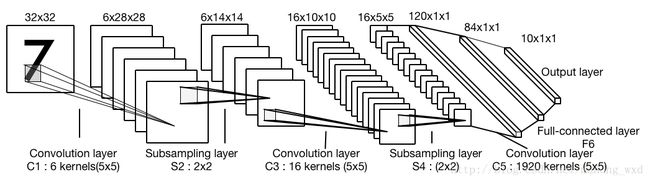
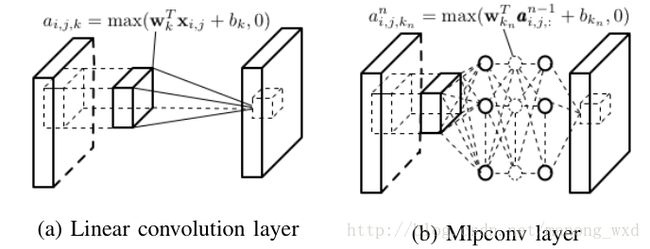
卷积层的目的是学习输入数据的特征表达形式。正如图1所示，卷积层由多个卷积核组成，卷积核是用来计算不同的特征图的。特别是，一张特征图的每一个神经元与前一层一个区域的神经元相连接。这里的区域指的是该神经元在前一层的感受野。新的特征图可以通过一个学习到的卷积核在输入图像上第一次卷积得到，然后在卷积结果上使用元素级的非线性激活函数。通过使用一些不同的卷积核，就可以获得完整的新特征图。数学上，第l层卷积层的第k张特征图的区域(i,j)特征值 zli,j,k ，可以通过下面公式计算得到：

zli,j,k=wlkTxli,j+blk(1)

wlk 和 blk 是第l层卷积层第k个滤波器的权重向量和偏置， x(i,j)l 是第l层输入区域(i,j)的中心。请注意，产生特征图 zl:,:,k 的核 wlk 是共享的。这样的权值共享机制可以减少模型的复杂度，也使得网络更加容易训练。激活函数给CNN引入了非线性因素，使得多层网络可以更容易的检测非线性特征。让a(∙)表示非线性激活函数。卷积特征 zli,j,k 的激活值 ali,j,k 计算公式如下：

ali,j,k=a(zli,j,k)(2)

sigmoid、tanh和ReLU是典型的激活函数。Pooling层的目的是通过降低特征图的分辨率来实现平移不变性。它通常放在两个卷积层之间。Pooling层的每一张特征图都和它对应的前一层卷积层的特征图连接。用pool(∙)来表示pooling函数，对于每一张特征图 al:,:,k ，我们有：

yli,j,k=pool(am,n,kl),∀(m,n)∈Rij(3)

Rij 是区域(i,j)的局部邻域。典型的pooling操作为average pooling和max pooling。通过一些卷积层和pooling层的堆叠，我们可以提取更多的抽象特征表现形式。

经过一些卷积层和pooling层后，会接着一或多层全连接层，它们是用来进行高层推理的。它们将前一层的全部神经元和当前层的全部神经元进行连接，产生全局语义信息。最后一层全连接层的输出是输出层的输入。对于分类任务，softmax操作是最常用的。另一个常用的方法是SVM，它可以和CNN特征结合来解决不同的分类任务。让θ表示一个CNN的全部参数（例如：权重向量和偏置）。通过最小化特定任务的损失函数可以获得该任务的最佳参数。假设我们有N个想要的input-output的关系 {(xn,yn);n∈[i,...,N]} ， x(n) 为第n个输入数据， y(n) 是它的对应目标标签， o(n) 是CNN的输出。CNN的损失函数计算公式如下：

L=1N∑n=1Nℓ(θ;y(n),o(n))(4)

图2：线性卷积层和mlpconv卷积层的对比

训练一个CNN是一个全局优化的问题。通过最小化损失函数，我们可以找到最适合的一组参数。随机梯度下降法是优化CNN网络的最常用解决方法。