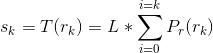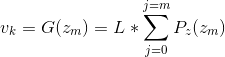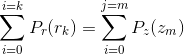直方图匹配
1. 概述
直方图匹配也叫做直方图规定化,是将某个图像的灰度分布按照某个特定的模式去变换的操作。
我们常常用到直方图均衡化,直方图均衡化是在整个灰度阶范围内对图像进行拉升;但是有的时候,这种整个范围内的拉升也许并不是最好的,我们可能会需要其按照某个灰度分布去进行拉升,也就需要用到上面提到的直方图均衡化/规定化。
2. 步骤
使用到直方图匹配的场景,我们必须知道目的图像,或者目的图像的灰度分布。直方图匹配的步骤如下:
1. 对原始图像进行直方图均衡化:![]()
2.假定对求得的图像,也就是规定化之后的图像进行直方图均衡化:![]()
3. 因为都是进行直方图均衡化,所以有![]() ,于是有
,于是有![]()
更具体的:
3. 规定化操作的目的就是要找到一个从原始图像到规定化之后图像的映射,积,从![]() 之间的映射关系。
之间的映射关系。
3. 从上面的分析可知:![]() ,有
,有
从公式可以看出,要求出![]() 之间的映射关系,只要满足
之间的映射关系,只要满足![]() 和
和![]() 的累计概率最相近即可。
的累计概率最相近即可。
3. 代码
代码步骤:
- 计算源图像的累计直方图;
- 计算规定图像的累计直方图;
- 计算源图像累计直方图各个灰度阶到规定图像的累计直方图各个灰度阶的差的绝对值;
- 求出步骤3中各阶中绝对值对应的最小值,最小值对应的灰度阶即为映射后的值。
# coding: utf-8
import cv2
import numpy as np
def show_gray_img_hist(hist, window_title):
"""
:param hist: 灰度图像的直方图,为一个256*1的 numpy.ndarray
:return: none
"""
min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(hist)
hist_img = np.zeros([256, 256], np.uint8)
for h in range(256):
intensity = int(256 * hist[h] / max_val)
cv2.line(hist_img, (h, 256), (h, 256 - intensity), [255, 0, 0])
cv2.imshow(window_title, hist_img)
def get_acc_prob_hist(hist):
acc_hist = np.zeros([256, 1], np.float32)
pre_val = 0.
for i in range(256):
acc_hist[i, 0] = pre_val + hist[i, 0]
pre_val = acc_hist[i, 0]
acc_hist /= pre_val
return acc_hist
def hist_specify(src_img, dst_img):
"""
直方图规定化,把dst_img按照src_img的图像进行规定化
:param src_img:
:param dst_img:
:return:
"""
# 计算源图像和规定化之后图像的累计直方图
src_hist = cv2.calcHist([src_img], [0], None, [256], [0.0, 255.])
dst_hist = cv2.calcHist([dst_img], [0], None, [256], [0.0, 255.])
src_acc_prob_hist = get_acc_prob_hist(src_hist)
dst_acc_prob_hist = get_acc_prob_hist(dst_hist)
# 计算源图像的各阶灰度到规定化之后图像各阶灰度的差值的绝对值,得到一个256*256的矩阵,第i行表示源图像的第i阶累计直方图到规定化后图像各
# 阶灰度累计直方图的差值的绝对值,
#diff_acc_prob = np.ndarray((256, 256), np.float32)
#for i in range(256):
# for j in range(256):
# diff_acc_prob[i, j] = abs(src_acc_prob_hist[i] - dst_acc_prob_hist[j])
diff_acc_prob = abs(np.tile(src_acc_prob_hist.reshape(256, 1), (1, 256)) - dst_acc_prob_hist.reshape(1, 256))
# 求出各阶灰度对应的差值的最小值,该最小值对应的灰度阶即为映射之后的灰度阶
table = np.argmin(diff_acc_prob, axis=0)
table = table.astype(np.uint8) # @注意 对于灰度图像cv2.LUT的table必须是uint8类型
#将源图像按照求出的映射关系做映射
result = cv2.LUT(dst_img, table)
# 显示各种图像
show_gray_img_hist(src_hist, 'src_hist')
show_gray_img_hist(dst_hist, 'dst_hist')
cv2.imshow('src_img', src_img)
cv2.imshow('dst_img', dst_img)
cv2.imshow('result', result)
result_hist = cv2.calcHist([result], [0], None, [256], [0.0, 255.])
show_gray_img_hist(result_hist, 'result_hist')
if __name__ == '__main__':
src_img = cv2.imread('D:/lena.jpg', 0)
dst_img = cv2.imread('D:/moon.jpg', 0)
hist_specify(src_img, dst_img)
cv2.waitKey()
运行结果如下:
从做到右边分别为模板图像的直方图,原始图像的直方图,模板图像,原始图像,规定化之后的结果,规定化之hi偶的直方图。