《西瓜书》笔记09:聚类
1.聚类任务
无监督学习:训练样本的标记信息是未知的。目标是通过对无标记样本的学习揭示数据内在性质,为进一步数学分析提供基础。
此类学习任务中研究最多,应用广泛的是聚类。
聚类:试图将数据集中的样本划分为若干个通常互不相交的子集。每个子集称为一个簇(cluster)。
每个簇可能对应于一些潜在概念。这些概念对于聚类算法而言事先未知。聚类过程仅能自动形成簇结构。簇所对应的概念语义需有使用者把握。
聚类可作为一个单独过程,也可作为分类等其他任务的先驱。比如商户定义用户类型不太容易,可先聚类根据结果将每个簇定义一个类,再基于这些类训练分类模型,用于判别新用户。
2.性能度量
聚类性能:评估聚类好坏。
直观的:簇内相似度高,簇间相似度低。
大致分为两类:
- 与某个参考模型比较,如该领域专家给出的划分结果。
- 不利用外部指标而直接考察聚类结果
对数据集D,假定聚类给出的簇为 C1,C2,...,Ck 。参考模型给出一个簇划分 C∗ 。将样本两两配对,我们定义四个集合:
- a:在C中同簇,C*中也同簇
- b:在C中同簇,C*中不同簇
- c:在C中不同簇,C*中同簇
- d:在C中不同簇,C*也不同簇
导出一些常用的聚类性能外部指标:
- Jaccard系数: JC=aa+b+c
- FM指数:待续
- …
上述性能度量结果在[0, 1]之间,值越大越好。
对于聚类结果的簇划分,可有:
- avg(C):簇C内样本间的平均距离
- diam(C):簇C内样本间的最远距离
- dmin(Ci, Cj):两个簇最近的样本间的距离
- dcen(Ci,Cj):两个簇中心点间的距离
由上述推导出常用的聚类性能内部指标:
- DB指数:分子簇内平均距离,分母为簇中心间距离,其最大值。越小越好
- Dunn指数:分子为簇间最近样本距离,分母为簇间最远样本距离,其最小值。越大越好。
3.距离计算
两个向量i和j,最常用的是闵可夫斯基距离,即(i-j)的Lp范数。
p = 1,曼哈顿距离
p = 2,欧氏距离
连续属性,即数值属性,可直接用距离计算。
离散属性,即列名属性,无序属性,不能直接用闵可夫斯基距离计算。采用VDM(value difference metric),某属性上取不同值时的所占比例的差的Lp范数。
4.原型聚类
基于原型的聚类。假设聚类结构能通过一组原型刻画,所谓原型,指的是样本空间具有代表性的点。
通常,此类聚类算法先对原型初始化,然后对原型进行迭代更新求解。采用不同的原型表示,不同的求解方式,产生不同的算法。
4.1 k-means聚类
最小化平方误差:
下标2表示L2范数,根号下的平方和。右上角2表示去掉根号,则是平方和。
E刻画了簇内样本间的围绕簇均值向量的紧密程度,E值越小簇内样本值相似度越高。
最小化E是个NP难问题。K均值算法采用贪心策略,迭代优化来近似求解。
k-means算法
输入:样本集D,聚类簇数k
输出:簇划分
过程:
(1)从D中选择k个样本作为初始均值向量
(2)while(当前均值向量不更新时)
(2-1)遍历各样本,计算样本与k个均值向量的距离。距离最小的均值向量确定样本的簇标记。将样本划分至对应簇。
(2-2)遍历k个簇。计算每个簇新的均值向量。如果不等于之前的则更新,否则保持不变。
直至各均值向量不再更新。或者达到最大运行轮数,或者最小调整阈值内。
3.2 学习向量量化
LVQ假设数据样本带有类别标记。学习时利用样本的这些监督信息来辅助聚类。
…
3.4 高斯混合聚类
与k均值,LVQ用原型向量来刻画聚类结构不同,高斯混合聚类采用概率模型来表达聚类原型。
常采用EM算法进行迭代优化求解。
3.5 密度聚类
基于密度的聚类(density-based clustering)
假设聚类结构能通过样本分布的紧密程度(距离度量)确定。通常,密度聚类算法从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断靠站聚类簇以获得最终结果。
DBSCAN(Density-based spatial clusting of applications with noise)
其基于一组邻域参数,刻画样本分布的紧密程度。
如上图,虚线表示邻域。令minpts=3,则x1是核心对象(邻域至少包含Min个样本),邻域内的点为密度直达点(x2)。通过密度直达的非相邻点(x3)为密度可达点。若两个点之间存在一个点x1,分别可以密度可达这两个点,则这两点成为密度相连(x3,x4)。
DBSCAN将簇定义为:由密度可达关系导出的最大的密度相连样本集合。
即该簇内,任意两点为密度相连。且能密度可达的点都包含进来了。
DBSCAN算法:
输入:样本集D,邻域参数(距离,Minpts)
输出:簇划分
过程:
(1)初始化核心对象集为空
(2)对样本集对象遍历。对每一个点,确定其领域内的点个数,若大于Min则加进核心对象。
(3)初始化簇数k=0,未访问样本集合D。
while(未访问样本集合为空)
随机选择一个核心对象为种子,找出由他可密度可达的所有样本,这就构成了第一个聚类簇。然后将该聚类簇中的对象,从核心对象中去除。再从核心对象更新集中选择种子生成下一个聚类簇。
不断重复,直至核心对象集为空,while结束。
可以想象,当簇比较紧密时,则算法倾向于将其作为一个簇,越紧密,好像密度越大,估计这就是名称的来历。簇若比较散,则除了邻域,不会合并。
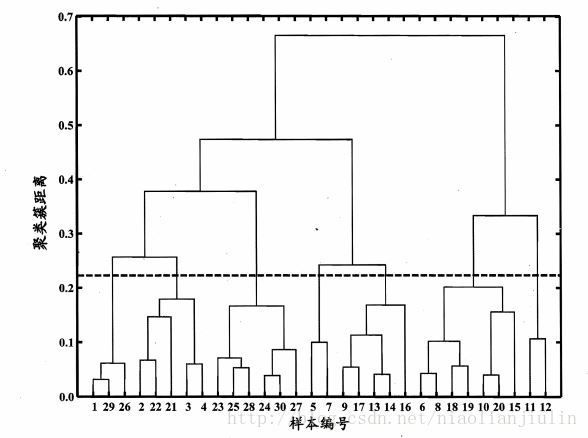
3.6 层次聚类
hierarchical clustering。不同层次上对数据集进行划分,从而形成树形的聚类结构。划分可采用自底向上的聚合策略。也可采用自顶向下的分拆策略。
AGNES(AGglomerative NESting,成团的嵌套),自底向上聚合
先将每个样本看做一个初始聚类簇,然后算法运行的每一步中找出距离最近的两个聚类簇进行合并,不断重复,直至达到预设的聚类簇个数。
如何计算两个聚类簇之间的距离?每个簇是样本集合,采用关于集合的某种距离即可。
- 最小距离:两个簇的最近样本的距离
- 最大距离:两个簇的最远样本的距离
- 平均距离:两个簇的是所有样本互连后计算平均距离
两个簇的最小距离:红线
两个簇的最大距离:黑线
两个簇的平均距离:两边全连接[4*4]后算平均(sum_dist/[4*4])
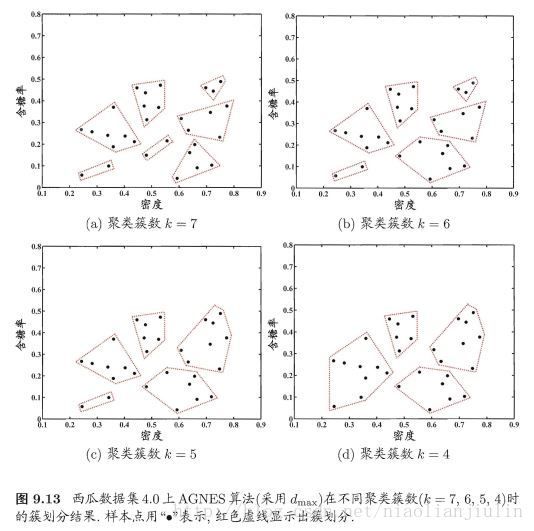
三种距离下,AGNES分别称为单链接,全链接,均链接算法。
聚类的新算法出现最多,最快。其不存在客观标准。