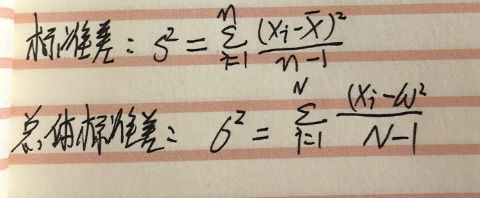机器学习中要用到的数学知识之统计学(一)
从目前自己所掌握的关于机器学习后深度学习的知识中关于数学的相关知识发现还是统计学的概念和公式用的最多的,所以我就先将这一部分的相关知识总结罗列一下,对于一些数学基础比较薄弱的童鞋应该算是比较容易入门机器学习的,只是在你听到方差样本和概率密度这些词的时候不会一脸懵逼。
当然有些最基本的概念性的东西我就不去过多解释了,自己可以去百度。
一些基本概念:
1.中位数和众数:一组数中位于中间的数就称为中位数(排序好的);一组数中出现次数最多的那个数就称为众数
示例:
a=[1,2,3,2,3,4,5]
数列a中的中位数就是2,众数是2跟3
b=[1,2,3,4,9,6,2,5]
数列b中的中位数就是4与9的均值,众数是2
2.极差和中程数:一组数中最大数与最小数之间的距离就是极差;一组数中最大数与最小数求平均得到的数就是中程数。
示例:
上面a数列的极差就是5-1=4,中程数就是(1+5)/2=3 (好吧,不知道这里咋写数学公式,后面的数学公式实在不行我就在纸上写出来拍图贴上来)
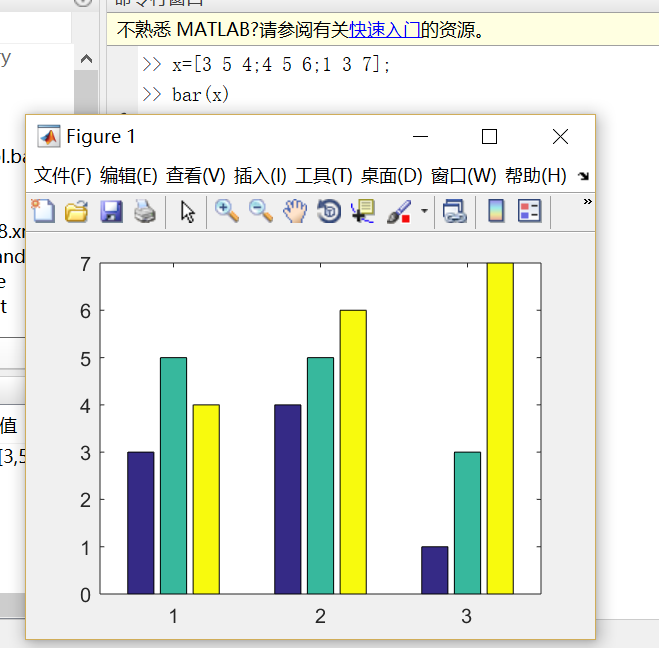
3.条形统计图(自己要学会MATLAB里的常用绘图函数)
上面就是一个三维数组的条形图
在后面讲到到概率密度函数的时候会演示如何绘制概率密度的统计条形图
4.线型图
就是用plot函数,同matplotlib一致
示例:(MATLAB中)
x=0:0.02*pi:2*pi
y1=sin(x)
y2=cos(x)
plot(x,y1,'b',x,y2,'g')
4.饼图
a=[10 20 30 40]
pie(a) //绘制饼图
exp=[0 1 0 1]
pie3(a,exp) //绘制三维饼图
5.盒须图-->数据的散布情况,它的具体定义自己百度去,(这个做大数据分析时应该会用到)
xrandn(100,25)
subplot(2,1,1)
boxplot(x)
就是用plot函数,同matplotlib一致
示例:(MATLAB中)
x=0:0.02*pi:2*pi
y1=sin(x)
y2=cos(x)
plot(x,y1,'b',x,y2,'g')
4.饼图
a=[10 20 30 40]
pie(a) //绘制饼图
exp=[0 1 0 1]
pie3(a,exp) //绘制三维饼图
5.盒须图-->数据的散布情况,它的具体定义自己百度去,(这个做大数据分析时应该会用到)
xrandn(100,25)
subplot(2,1,1)
boxplot(x)
6.集中趋势-->描述性统计学
描述性统计学中一组数据的集中趋势就是通过算术平均数,中位数和众数来体现
eg:1 1 2 3 4
它的中位数是2 众数是1,算术平均数是2.2 所以它的集中趋势是2
eg:3 3 3 3 100
100只在其中出现一次,众数是3,中位数也是3,所以它的集中趋势是3,100就称为离群值
描述性统计学中一组数据的集中趋势就是通过算术平均数,中位数和众数来体现
eg:1 1 2 3 4
它的中位数是2 众数是1,算术平均数是2.2 所以它的集中趋势是2
eg:3 3 3 3 100
100只在其中出现一次,众数是3,中位数也是3,所以它的集中趋势是3,100就称为离群值
7.样本和总体
假设有一班级,那我们可以把这个班级的学生总和当做一个总体,设为Am,这个Am就是总体,而我们再从这个班级中随机选择5个学生,那么这5个学生就可以组成一个随机样本Sam,这就是样本和总体的概念
8.总体方差-->体现的是总体的离中趋势,相比较集中趋势,它更能展现数据的特性
9 .样本方差
结合上面的假设,设这个Sam里的个体分别是x1,x2,x3,x4,x5,这个样本里的个体都有很多的特征,现在我们只取一个特征,如学生的身高来统计
结合上面的假设,设这个Sam里的个体分别是x1,x2,x3,x4,x5,这个样本里的个体都有很多的特征,现在我们只取一个特征,如学生的身高来统计
PS:在Word里编写的数学公式无法拷贝出来,所以只能看我手写的啦,字丑莫介意。