1、先思考下面的表达式怎么实现
先思考下面的表达式如何计算,虽然可以直接计算,但是怎么实现的呢?
请输入一个表达式
计算式:[7*2*2-5+1-5+3-3]
我们可以用栈来实现,怎么实现?先看一个复杂的实现方式:中缀表达式实现
2、什么是中缀表达式?
中缀表达式就是人们生活中的计算方法,比如上面的表达式,我们怎么算?7*2*2-5+1-5+3-3,在计算机中也是这样,我们先看如何实现它
3、中缀表达式计算器代码实现和讲解
3.1先定义一个栈(自定义)
//先创建一个栈,直接使用前面创建好 //定义一个 ArrayStack2 表示栈, 需要扩展功能 class ArrayStack2 { private int maxSize; // 栈的大小 private int[] stack; // 数组,数组模拟栈,数据就放在该数组 private int top = -1;// top表示栈顶,初始化为-1 //构造器 public ArrayStack2(int maxSize) { this.maxSize = maxSize; stack = new int[this.maxSize]; } //增加一个方法,可以返回当前栈顶的值, 但是不是真正的pop public int peek() { return stack[top]; } //栈满 public boolean isFull() { return top == maxSize - 1; } //栈空 public boolean isEmpty() { return top == -1; } //入栈-push public void push(int value) { //先判断栈是否满 if(isFull()) { System.out.println("栈满"); return; } top++; stack[top] = value; } //出栈-pop, 将栈顶的数据返回 public int pop() { //先判断栈是否空 if(isEmpty()) { //抛出异常 throw new RuntimeException("栈空,没有数据~"); } int value = stack[top]; top--; return value; } //显示栈的情况[遍历栈], 遍历时,需要从栈顶开始显示数据 public void list() { if(isEmpty()) { System.out.println("栈空,没有数据~~"); return; } //需要从栈顶开始显示数据 for(int i = top; i >= 0 ; i--) { System.out.printf("stack[%d]=%d\n", i, stack[i]); } } //返回运算符的优先级,优先级是程序员来确定, 优先级使用数字表示(额外添加,方便后面调用) //数字越大,则优先级就越高. public int priority(int oper) { if(oper == '*' || oper == '/'){ return 1; } else if (oper == '+' || oper == '-') { return 0; } else { return -1; // 假定目前的表达式只有 +, - , * , / } } //判断是不是一个运算符(额外添加,方便后面调用) public boolean isOper(char val) { return val == '+' || val == '-' || val == '*' || val == '/'; } //计算方法(额外添加,方便后面调用) public int cal(int num1, int num2, int oper) { int res = 0; // res 用于存放计算的结果 switch (oper) { case '+': res = num1 + num2; break; case '-': res = num2 - num1;// 注意顺序 break; case '*': res = num1 * num2; break; case '/': res = num2 / num1; break; default: break; } return res; } }
3.2具体实现
public class Calculator { public static void main(String[] args) { //根据前面老师思路,完成表达式的运算 String expression = "7*2*2-5+1-5+3-4"; // 15//如何处理多位数的问题? //创建两个栈,数栈,一个符号栈 ArrayStack2 numStack = new ArrayStack2(10); ArrayStack2 operStack = new ArrayStack2(10); //定义需要的相关变量 int index = 0;//用于扫描 int num1 = 0; int num2 = 0; int oper = 0; int res = 0; char ch = ' '; //将每次扫描得到char保存到ch String keepNum = ""; //用于拼接 多位数 //开始while循环的扫描expression while(true) { //依次得到expression 的每一个字符 ch = expression.substring(index, index+1).charAt(0); //判断ch是什么,然后做相应的处理 if(operStack.isOper(ch)) {//如果是运算符 //判断当前的符号栈是否为空 if(!operStack.isEmpty()) { //如果符号栈有操作符,就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符,就需要从数栈中pop出两个数, //在从符号栈中pop出一个符号,进行运算,将得到结果,入数栈,然后将当前的操作符入符号栈 if(operStack.priority(ch) <= operStack.priority(operStack.peek())) { num1 = numStack.pop(); num2 = numStack.pop(); oper = operStack.pop(); res = numStack.cal(num1, num2, oper); //把运算的结果如数栈 numStack.push(res); //然后将当前的操作符入符号栈 operStack.push(ch); } else { //如果当前的操作符的优先级大于栈中的操作符, 就直接入符号栈. operStack.push(ch); } }else { //如果为空直接入符号栈.. operStack.push(ch); // 1 + 3 } } else { //如果是数,则直接入数栈 //numStack.push(ch - 48); //? "1+3" '1' => 1 //分析思路 //1. 当处理多位数时,不能发现是一个数就立即入栈,因为他可能是多位数 //2. 在处理数,需要向expression的表达式的index 后再看一位,如果是数就进行扫描,如果是符号才入栈 //3. 因此我们需要定义一个变量 字符串,用于拼接 //处理多位数 keepNum += ch; //如果ch已经是expression的最后一位,就直接入栈 if (index == expression.length() - 1) { numStack.push(Integer.parseInt(keepNum)); }else{ //判断下一个字符是不是数字,如果是数字,就继续扫描,如果是运算符,则入栈 //注意是看后一位,不是index++ if (operStack.isOper(expression.substring(index+1,index+2).charAt(0))) { //如果后一位是运算符,则入栈 keepNum = "1" 或者 "123" numStack.push(Integer.parseInt(keepNum)); //重要的!!!!!!, keepNum清空 keepNum = ""; } } } //让index + 1, 并判断是否扫描到expression最后. index++; if (index >= expression.length()) { break; } } //当表达式扫描完毕,就顺序的从 数栈和符号栈中pop出相应的数和符号,并运行. while(true) { //如果符号栈为空,则计算到最后的结果, 数栈中只有一个数字【结果】 if(operStack.isEmpty()) { break; } num1 = numStack.pop(); num2 = numStack.pop(); oper = operStack.pop(); res = numStack.cal(num1, num2, oper); numStack.push(res);//入栈 } //将数栈的最后数,pop出,就是结果 int res2 = numStack.pop(); System.out.printf("表达式 %s = %d", expression, res2); } }
以上代码看懂就行,这是个复杂的解法
缺点:
1、需要先判断优先级
2、两个栈进行存储
3、不适合计算机计算
优点:
方便我们生活中计算
为了方便计算机计算,可用后缀表达式
4、后缀表达式(逆波兰式)
后缀和中缀的比较
后缀和中缀的比较:1、无需每次都判断优先级 2、一个栈可实现 3、逻辑简单
中缀转后缀
我们使用后缀,需要先明白中缀怎么转后缀(生活中表达式转后缀):
1、先建立两个栈,一个是s1(符号栈),一个是s2(数栈) 2、从左向右扫描表达式 3、遇到数直接压入s2 4、遇到符号,进行判定: 4.1 S1为空,直接压入 4.2 不为空,和栈顶符号比较优先级: 4.1.1 若优先级比栈顶符号高,压入S1 4.1.2 若优先级比栈顶符号低,栈顶符号取出压入S2,添加的符号转到4重新判定 4.1.3 遇到括号: 4.1.3.1 左括号( 直接压入S1 4.1.3.2 右括号 ),将S1栈顶元素逐个弹出压入S2,直到遇见左括号 ( 抵消 5、扫描完后,将S1符号压入S2,并逆序弹出,得到的就是后缀表达式
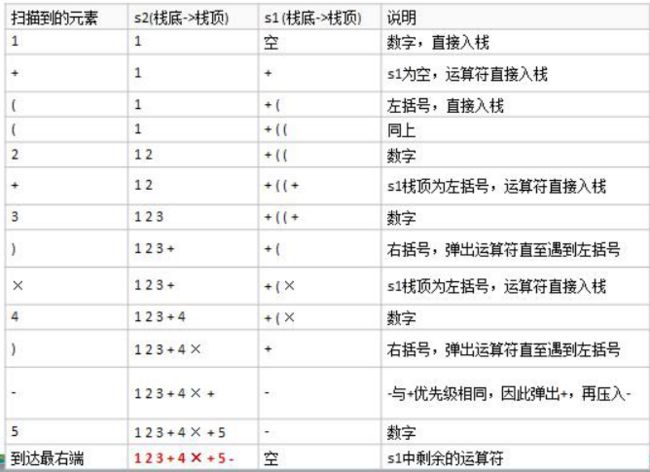
举例:将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式
代码实现
表达式放入集合
先把表达式字符串转成list类型,方便存取(不用数组是因为数组需要下标索引,还要定义长度,不方便)
//根据表达式传入集合 public static ListtoSuffixExpression(String expression) { List list = new ArrayList<>(); int i = 0; //判断长度是否超过 String str; //拼接多位数,如30 char ch = ' '; //存放从集合取出的单个字符 do { ch = expression.charAt(i); if (ch < 48 || ch > 57) { //根据ASCii表,48~57是数字 list.add("" + ch); //前面加“”更方便转成string类型 i++; } else { str = ""; //为什么不在方法开始初始化?因为str是拼接多位数,放在方法开始循环的时候会一直添加,所以需要再局部初始化 while (i < expression.length() && (ch = expression.charAt(i)) >= 48 && (ch = expression.charAt(i)) <= 57) { str += ch; i++; } list.add(str); } } while (i < expression.length()); return list; }
中缀转成后缀
//转成后缀 public static ListparseSuffixExpression(List ls) { //准备两个栈 Stack S1 = new Stack<>(); //符号栈 List S2 = new ArrayList<>(); //数栈 for (String item : ls) { if (item.matches("\\d+")) { //如果是数字(正则表达式),加入数栈 S2.add(item); } else if (item.equals("(")) {//如果是(,加入符号栈 S1.push(item); } else if (item.equals(")")) { //如果是),弹出符号栈符号直到和(抵消 while (!S1.peek().equals("(")) { S2.add(S1.pop()); } S1.pop(); //消除( } else { while (S1.size()!=0 && Operation.getValue(S1.peek()) >=Operation.getValue(item) ){//比较符号的优先级 S2.add(S1.pop()); } //再将item压入 S1.push(item); } } //执行完后,如果符号栈不为空,就加入数栈 while (S1.size()!=0){ S2.add(S1.pop()); } return S2; } }
判断优先级(Operation类)
class Operation{ private static int ADD=1; private static int SUB=1; private static int MUL=2; private static int DIV=2; public static int getValue(String oper){ int result=0; switch (oper){ case "+": result= ADD; break; case "-": result= SUB; break; case "*": result= MUL; break; case "/": result= DIV; break; default: new RuntimeException("输入符号异常"); } return result; }
后缀表达式计算
public static int calculate(Listls) { Stack stack = new Stack<>(); for (String item : ls) { if (item.matches("\\d+")) {//匹配的是数字 //入栈 stack.push(item); } else {//如果不是数字,取数字计算 int num2 = Integer.parseInt(stack.pop()); int num1 = Integer.parseInt(stack.pop()); int res = 0; switch (item) { case "+": res = num1 + num2; break; case "-": res = num1 - num2; break; case "*": res = num1 * num2; break; case "/": res = num1 / num2; break; default: throw new RuntimeException("运算符有误"); } stack.push(String.valueOf(res)); } } return Integer.parseInt(stack.pop()); }