Neural networks and deep learning阅读笔记（2）后向传播算法

Neural networks and deep learning阅读笔记（2）后向传播算法

上一章主要是梯度下降算法，但是如何计算cost function的梯度没有详细讲，这一章就主要讲了一种计算梯度的算法——backpropagation后向传播算法。这一章有很多数学emmm慢慢推吧，后向传播还是蛮重要的

Warm up

w_jk^l如图所示代表了从（l-1）层的第k个神经元到第l层第j个神经元的权重。b_j^l代表了第l层第j个神经元的偏置，a_j^l代表了第l层第j个神经元的激活值，也就是输入经过sigmoid函数之后的值。所以每一层的激活值可以用上一层的激活值表示：

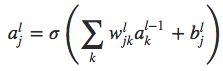
我们将这三个值分别用一个矩阵w^l，两个向量a^l、b^l来表示。并且sigmoid函数可以对向量中的每一个元素进行映射，所以上式可以如下表示：

我们将括号里的内容记为z^l，称为加权输入weighted input，所以a^l=$\sigma$(z^l)。

对于损失函数的两个假设

第一个假设就是总损失函数C可以被写成每一个训练样本的损失函数的平均，即C=$\frac{1}{n}\Sigma$_xC_x。其中C_x=$\frac{1}{2}$||y-a^L||²。实际上后向传播算法计算了单个样本的损失函数对权重、偏置的偏微分，然后取平均，所以我们需要这样一个假设。
第二个假设就是损失函数可以写成输出的函数，即C=C(a^L)。

Hadamard product

我们使用$\odot$这个算子表示两个同维度的向量elementwise的乘积，即对应的元素相乘得到新的向量。

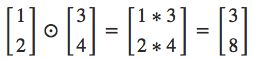
four fundamental equations

首先作者引入了一个变量$\delta$_j^l，代表第l层第j个神经元的误差error，后向传播算法就是先计算error，然后将误差与$\partial$C/$\partial$w_jk^l和$\partial$C/$\partial$b_j^l联系起来。error的定义如下：

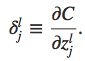
error in the output layer: $\delta$^L

(BP1):
右边$\partial$C/$\partial$a_j^L以第j个输出激活值的函数描述了损失变化的快慢。第二项$\sigma$’(z_j^L)描述了激活函数关于z_j^L变化的快慢。相乘则是损失关于z_j^L变化的快慢。
值得注意的是，上式中每一项都比较容易计算。
如果将$\delta$用矩阵形式来表示：

$▽$_aC代表了C关于a的输出激活值的变化快慢。由C的公式我们可以算出$▽$_aC=(a^L-y)，所以公式BP1变成为：

$\delta$^l in terms of $\delta$^l+1

(BP2):

啊，懵…假设我们知道了l+1层的error，可以想象这个式子是向后传播error到第l层。
所以我们首先用BP1计算$\delta$^L，然后用BP2计算$\delta$^L-1、$\delta$^L-2……

for the rate of change of the cost with respect to any bias in the network

(BP3):

error正好等于损失对偏置的偏导。

for the rate of change of the cost with respect to any weight in the network

(BP4):

这个式子可以用下面一张图来帮助理解：

当a_in很小的时候，$\partial$C/$\partial$w也会很小，代表了权重学习很慢。
sigmoid函数在接近0或者1的时候图像是很平缓的，所以其在0或者1附近的导数约等于0。这个时候权重学习很慢，我们称输出神经元饱和saturated。偏置也是同样的情况。

作者说不期望我们第一次就完全理解这四个式子，不理解的话看一下之后的proof，我自己看了一遍proof，之后做了笔记
四个式子整理如下：

proof：
首先从BP1开始，之前我们定义了：

根据链式法则，我们可以改写成如下形式：

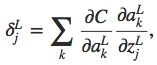
k是输出层所有的神经元。而输出激活值a_k^L仅基于此神经元的输入值z_j^L，所以当k≠j时，$\partial$a_k^L/$\partial$z_j^L就没有啦~所以上式简化成

而a_j^L=$\sigma$(z_j^L)，所以右边第二项可以简化成$\sigma$’(z_j^L)，上式即变为BP1。
下面是BP2的证明，使用链式法则：


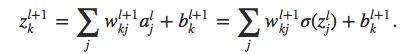
所以上式第二项可以表示成：

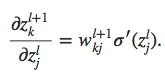
将其带入$\delta$_j^l的表达式即可得到BP2。
BP3、BP4作者留作练习了，不过都是用链式法则证明的，可以自己推一下。

The backpropagation algorithm

1. Input
   x：设置输入层相应的激活值a¹
2. Feedforward
   对于l=2,3,…,L，计算z^l=w^la^l-1+b^l和a^l=$\sigma$(z^l)
3. Output error
   $\delta$^L：计算向量$\delta$^L=$▽$_aC $\odot$ $\sigma$'(z^L)
4. Backpropagate the error
   对于每一层l=L-1, L-2, …, 2，用BP2计算前一层error
5. Output
   损失函数的梯度可以用以下两式计算。
   
   

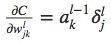
The code for bp

搓手手~~
上一章是定义了一个minimatch

def update_mini_batch(self, mini_batch, eta):
	nabla_b = [np.zeros(b.shape) for b in self.biases]
	nabla_w = [np.zeros(w.shape) for w in self.weights]
	for x, y in mini_batch:
		delta_nabla_b, delta_nabla_w = self.backprop(x, y)
		nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
		nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
	self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)]
	self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)]

所以重点其实只有一句话

delta_nabla_b, delta_nabla_w = self.backprop(x, y)

来，我们再把bp算法复习一遍~

def backprop(self, x, y):
	nabla_b = [np.zeros(b.shape) for b in self.biases]
	nabla_w = [np.zeros(w.shape) for w in self. weights]
	# feedforward
	activation = x
	activations = [x] # list to store all the activations, layer by layer
	zs = [] # list to store all the z vectors, layer by layer
	for b, w in zip(self.biases, self.weights):
		z = np.dot(w, activation)+b
		zs.append(z)
		activation = sigmoid(z)
		activations.append(activation)
	# backward pass
	delta = self.cost_derivative(activations[-1], y) * \ sigmoid_prime(zs[-1])
	nabla_b[-1] = delta
	nabla_w[-1] = np.dot(delta, activations[-2].transpose())
	for l in xrange(2, self.num_layers):
		z = zs[-l]
		sp = sigmoid_prime(z)
		delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
		nabla_b[-l] = delta
		nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
	return (nabla_b, nabla_w)

def cost_detivative(self, output_activations, y):
	return (output_activations-y)

然后在Network这个class的外面再定义几个函数，计算sigmoid和其导数：

def sigmoid(z):
	return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
	return sigmoid(z)*(1-sigmoid(z))

哒啦~完成！