Ensemble Learning 之 Bagging 与 Random Forest

Bagging 全称是 Boostrap Aggregation，是除 Boosting 之外另一种集成学习的方式，之前在已经介绍过关与 Ensemble Learning 的内容与评价标准，其中“多样性”体现在应尽可能的增加基学习器的差别。Bagging 主要关注增大 “多样性”，他的做法是这样的，给定训练集  D D，对  D D 进行 Bootstrap 采样，得到若干个不同的子集，Bootstrap 会确保各个子集有一定的交集，分别在各个子集上训练得到基分类器并且组合起来共同进行决策。

Bootstrap 与 Bagging

Bootstrap Sampling 是一种统计学上的抽样方法，该方法是这样执行的，对于有  m m 个样本的数据集  D D，进行  m m 次有放回采样得到数据集  D′ D′ ，明显  D D 与  D′ D′ 大小相同，而且放回采样使得  D′ D′ 中有的样本重复出现，有的样本则没有出现，简单估计一下，某个样本在  m m 次采样中始终没被采到的概率为  (1−1m)m (1−1m)m ,取极限：

limm→∞(1−1m)m=1e≈0.368 limm→∞(1−1m)m=1e≈0.368

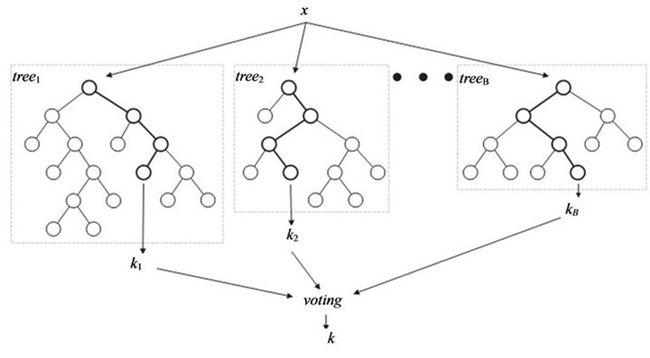
即  D D 中的样本大概有 63.2% 几率出现在  D′ D′ 中，采样出 B 个 Bootstrap 样本集  D1,D2,…,DB D1,D2,…,DB ，对这 B 个样本集分别训练一个基学习器  Tb(x) Tb(x) ，结合这些基学习器共同作出决策。决策时，在分类任务中通常采用投票法，若两个类别票数一样，最简单的做法是随机选择一个；而回归任务则一般使用平均法。整个流程如下所示：

综上给出 Bagging 的的学习算法：

输入：训练集 D={(xi,yi)}Ni=1 D={(xi,yi)}i=1N  与参数 B

1. 采样得到 B 个 Bootstrap 训练集： {Db}Bb=1. {Db}b=1B.

2.  for for  b=1,2,…B b=1,2,…B  do do:

      用 Bootstrap 训练集  Db Db 得到基学习器  Tb(x) Tb(x);

3. 组合 B 个学习器得到最终模型  T(x)=∑bTb(x) T(x)=∑bTb(x).

 

Bagging 较之 单学习器的效果会有很大提升，下图左为对 CART 进行 Bagging 后效果的提升，但是 Bagging 效果通常不如 Boosting ，下图右为两者的对比。

由于 Bagging 中各个基学习器独立进行，简直再适合并行不过了，而且速度非常快。

Random Forest

Random Forest 是建立在 Bagging 之上的概念，首先其做法类似于 Bagging ，通过 Bootstrap 采样得到 B 个不同的样本集，区别在于基学习器 Decision Tree 的建立，Random Forest 在训练基学习器的过程中进一步引入了随机属性选择，具体来说，假设当前待分裂节点有  d d 个特征，Bagging 中的决策树在分裂时会在所有  d d 个特征中选出一个最优特征用作划分特征；而 Random Forest 对于待分裂节点，先在  d d 个特征集集中随机选取包含  k k 个特征的子集，然后在这  k k 个子集中选择最优特征来划分数据集，这里参数  k k 控制了随机程度，若  k=d k=d ，则 Random Forest = Bagging ；若  k=1 k=1 则代表随机选取一个属性进行划分，这时效果会很差；一般性况下，推荐选取  k=log2d k=log2d 。Random Forest 额示意图如下，其实看不出与 Bagging 的差别。

随机森林建模过程

1. 假设我们设定训练集中的样本个数为N ，然后通过 Bootstrap Sampling 来获得 N 个有重复的样本集，这样的抽样结果将作为我们生成决策树的训练集；

2. 对于有 d 个特征的数据集，每个节点都将随机选择 k (k

3. 每棵决策树都最大可能地进行生长而不进行剪枝；

4. 通过对所有的决策树进行加总来预测新的数据（在分类时采用多数投票，在回归时采用平均）。

随机森林的优点：

1. 正如上文所述，随机森林算法能解决分类与回归两种类型的问题，并在这两个方面都有相当好的估计表现；

2. 随机森林可以做类似于 GBDT 那样的特征组合；

3. 在对缺失数据进行估计时，随机森林是一个十分有效的方法；

4. 当存在分类不平衡的情况时，随机森林能够提供平衡数据集误差的有效方法，比如对于 10:1 的数据，将多数数据分为 10份，做 10个 1:1 的单模型然后 Bagging 起来即可。

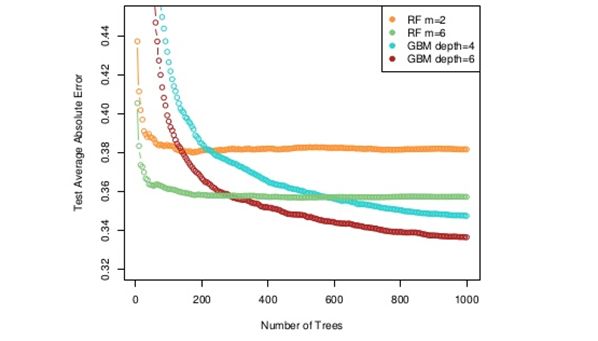
Random Forest 在许多任务上表现非常良好，而且易于实现、开销小，只对 Bagging 做了很小的改动，Bagging 中的“多样性”仅仅来自于对样本的扰动，而随机森林中加上了来自特征的扰动，正是由于这个改动，随机森林比 Bagging 拥有更小的泛化误差。而且使得基学习器更加“多样”。但 Random Forest 效果一般还是不如 Gradient Boosting ，如下图所示：

 

Bias and Variance 分析

从Bias 与 Variance 的角度来分析 Bagging 与 Boosting 的话，Bagging 是对样本重采样，对每一重采样得到的子样本集训练一个基学习器，最后取平均。由于子样本集的相似性以及使用的是同种学习器，因此各学习器有近似相等的 Bias 和 Variance（但学习器并不独立）。用 Bagging 组合 B 个模型，每个每个模型的损失用  Lb Lb 表示，所以Bagging 后的损失为所有学习器的均值：  1N∑bLb 1N∑bLb ，根据期望公式  E[X¯]=E[X] E[X¯]=E[X] :

E(1N∑bLb)=E(Lb)，b=1,2,…,B E(1N∑bLb)=E(Lb)，b=1,2,…,B

所以 Bagging 后的 Bias 和单个基学习器的接近，并不能显著降低bias，但是若各基学习器独立，根据  Var(X¯)=1NVar(X) Var(X¯)=1NVar(X) 则有:

Var(1N∑bLb)=1NVar(Lb)，b=1,2,…,B Var(1N∑bLb)=1NVar(Lb)，b=1,2,…,B

所以 Bagging 可以显著降低 Variance。实际上由于各个学习器并不是严格独立，所 Variance 的较少会小于 N 倍。

Boosting从优化角度来看，每一次迭代都比上一次更加精准，Adaboost 是从改变样本权值角度出发， Gradient Boosting 是从减小残差或者说从最大程度减小损失函数出发，所以 Boosting 主要还是靠降低 Bias 来提升预测精度。

综上， Boosting 降低 Bias ，Bagging 降低 Variance .