本文内容来自MIT_6.031_sp18: Software Construction课程的Readings部分,采用CC BY-SA 4.0协议。
由于我们学校(哈工大)大二软件构造课程的大部分素材取自此,也是推荐的阅读材料之一,于是打算做一些翻译工作,自己学习的同时也能帮到一些懒得看英文的朋友。另外,该课程的阅读资料中有的练习题没有标准答案,所给出的“正确答案”为译者所写,有错误的地方还请指出。
(更新:从第10章开始只翻译正确答案)
译者:李秋豪
审校:
V1.0 Sun Apr 1 22:23:37 CST 2018
本次课程的目标
今天我们会介绍以下几个思想:
- 不变量(invariants)
- 表示暴露(representation exposure)
- 抽象函数(abstraction functions)
- 表示不变量(representation invariants)
在这篇阅读中,我们会学习用一种正规的数学思想(抽象函数和表示不变量)去理解抽象数据类型ADT的实现。这些思想在软件设计的实践中非常重要。其中,抽象函数会让我们清晰的定义对两个ADT判断相等的操作(我们会在后面的课程中深入介绍),而表示不变量会让我们更易发现破坏数据结构导致的bug。
不变量
回想我们之前讨论过的关于ADT的内容,什么设计会产生好的ADT?其中最重要的一点就是它会保护/保留自己的不变量。 不变量是一种属性,它在程序运行的时候总是一种状态,而不变性就是其中的一种:一旦一个不变类型的对象被创建,它总是代表一个不变的值。当一个ADT能够确保它内部的不变量恒定不变(不受使用者/外部影响),我们就说这个ADT保护/保留自己的不变量.
当一个ADT保护/保留自己的不变量时,对代码的分析会变得更简单。例如,你能够依赖字符串不变性的特点,在分析的时候跳过那些关于字符串的代码;或者当你尝试基于字符串建立其他的不变量的时候,也会变得更简单。与此相对,对于可变的对象,你将不得不对每一处使用它的代码处进行审查。
不变性
在这篇阅读的后面,我们会看到许多关于不变量的例子,现在我们先看一看不变性:
/**
* This immutable data type represents a tweet from Twitter.
*/
public class Tweet {
public String author;
public String text;
public Date timestamp;
/**
* Make a Tweet.
* @param author Twitter user who wrote the tweet
* @param text text of the tweet
* @param timestamp date/time when the tweet was sent
*/
public Tweet(String author, String text, Date timestamp) {
this.author = author;
this.text = text;
this.timestamp = timestamp;
}
}我们应该怎么样做才能确保Tweet对象是不可变的(一旦被创建,author, message, 和 date都不能被改变)?
第一个威胁就是使用者可以直接访问Tweet内部的数据,例如:
Tweet t = new Tweet("justinbieber",
"Thanks to all those beliebers out there inspiring me every day",
new Date());
t.author = "rbmllr";这就是一个表示暴露(Rep exposure)的例子,就是说类外部的代码可以直接修改类内部存储的数据。上面的表示暴露不仅影响到了不变量,也影响到了表示独立性(译者注:“抽象数据类型”),如果我们改变类内部数据的表示方法,使用者也会受到影响。
幸运地是,Java给我们提供了处理这样的表示暴露的方法:
public class Tweet {
private final String author;
private final String text;
private final Date timestamp;
public Tweet(String author, String text, Date timestamp) {
this.author = author;
this.text = text;
this.timestamp = timestamp;
}
/** @return Twitter user who wrote the tweet */
public String getAuthor() {
return author;
}
/** @return text of the tweet */
public String getText() {
return text;
}
/** @return date/time when the tweet was sent */
public Date getTimestamp() {
return timestamp;
}
}其中, private 表示这个区域只能由同类进行访问;而final确保了该变量的索引不会被更改,对于不可变的类型来说,就是确保了变量的值不可变。
但是这并没有解决全部问题,表示还是会暴露!思考下面这个代码:
/** @return a tweet that retweets t, one hour later*/
public static Tweet retweetLater(Tweet t) {
Date d = t.getTimestamp();
d.setHours(d.getHours()+1);
return new Tweet("rbmllr", t.getText(), d);
}retweetLater 希望接受一个Tweet对象然后修改Date后返回一个新的Tweet对象。
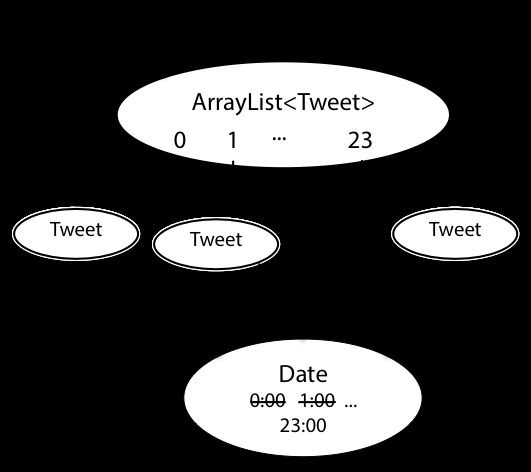
问题出在哪里呢?其中的 getTimestamp 调用返回一个一样的Date对象,它会被 t.t.timestamp 和 d 同时索引。所以当我们调用 d.setHours()后,t也会受到影响,如下图所示:
这样,Tweet的不变性就被破坏了。这里的问题就在于Tweet将自己内部对于可变对象的索引“泄露”了出来,因此整个对象都变成可变的了,使用者在使用时也容易造成隐秘的bug。
我们可以通过防御性复制来弥补这个问题:在返回的时候复制一个新的对象而不会返回原对象的索引。
public Date getTimestamp() {
return new Date(timestamp.getTime());
}可变类型通常都有一个专门用来复制的构造者,你可以通过它产生一个一模一样的复制对象。在上面的例子中,Date的复制构造者就接受了一个timestamp值,然后产生了一个新的对象。另一个复制可变对象的方法是使用clone() ,但是它没有被很多类支持(译者注:标准库里面只有5%支持),在Java中,使用clone()可能会带来一些麻烦。你可以在 Josh Bloch, Effective Java, item 11, 或者 Copy Constructor vs. Cloning获得更多有关这方面的信息。
现在我们已经通过防御性复制解决了 getTimestamp返回值的问题,但是我们还没有完成任务!思考这个使用者的代码:
/** @return a list of 24 inspiring tweets, one per hour today */
public static List tweetEveryHourToday () {
List list = new ArrayList();
Date date = new Date();
for (int i = 0; i < 24; i++) {
date.setHours(i);
list.add(new Tweet("rbmllr", "keep it up! you can do it", date));
}
return list;
} 这个代码尝试创建24个Tweet对象,每一个对象代表一个小时,如下图所示:
但是,Tweet的不变性再次被打破了,因为每一个Tweet创建时对Date对象的索引都是一样的。所以我们应该对创建者也进行防御性编程:
public Tweet(String author, String text, Date timestamp) {
this.author = author;
this.text = text;
this.timestamp = new Date(timestamp.getTime());
}通常来说,你要特别注意ADT操作中的参数和返回值。如果它们之中有可变类型的对象,确保你的代码没有直接使用索引或者直接返回索引。
你可能会提出异议。这样不会很浪费吗?毕竟你要复制创建这么多新的对象。为什么不直接在规格说明中解决这个问题:
/**
* Make a Tweet.
* @param author Twitter user who wrote the tweet
* @param text text of the tweet
* @param timestamp date/time when the tweet was sent. Caller must never
* mutate this Date object again!
*/
public Tweet(String author, String text, Date timestamp) {这种方法一般只在迫不得已的时候使用——例如,这个可变对象的数据量非常大,如果进行防御性复制的话会花费很多资源(当然,这取决于你对程序的判断)。如果不是极端情况,确保ADT会保留/保护自己的不变量总比通过规格说明来限定使用者要好。
而更好的解决方案是使用不可变类型。例如上面的例子中,如果我们使用的是 java.time.ZonedDateTime而非 java.util.Date, 那么我们只需要添加 private和final即可,不用再担心表示保留。
可变类型的不可变包装
Java的collections类提供了一种有趣的“折中”:不可变包装。
Collections.unmodifiableList() 会接收一个(可变)List然后将其包装为一个不可变对象——它的 set(), add(), remove(),等操作都会抛出异常。所以你可以将一个List包装为不可变对象(记得将以前对于List的索引丢掉),然后将它传入其他地方使用。
这种方法的缺点就是你只能在运行时获得不可变性,而不是编译时。Java不会在编译的时候对你对“不可变”列表的修改提出警告。但是这总比什么都不做好,所以使用不可变的列表、映射、和集合也是减少bug的好方法。
阅读小练习
Rep exposure
思考下面这个有问题的数据类型:
/** Represents an immutable right triangle. */
class RightTriangle {
/*A*/ private double[] sides;
/*B*/ public final int hypotenuse = 2;
/** Make a right triangle.
* @param legA, legB the two legs of the triangle
* @param hypotenuse the hypotenuse of the triangle.
*C* * Requires hypotenuse^2 = legA^2 + legB^2
* (within the error tolerance of double arithmetic)
*/
public RightTriangle(double legA, double legB, double hypotenuse) {
/*D*/ this.sides = new double[] { legA, legB };
/*D*/ this.hypotenuse = hypotenuse;
}
/** Get the two sides of the right triangle.
* @return two-element array with the triangle's side lengths
*/
public double[] getAllSides() {
/*E*/ return sides;
}
/** @param factor to multiply the sides by
* @return a triangle made from this triangle by
* multiplying all side lengths by factor.
*/
public RightTriangle scale(double factor) {
return new RightTriangle(sides[0]*factor, sides[1]*factor, hypotenuse*factor);
}
/** @return a regular triangle made from this triangle.
* A regular right triangle is one in which
* both legs have the same length.
*/
public RightTriangle regularize() {
double bigLeg = Math.max(side[0], side[1]);
return new RightTriangle (bigLeg, bigLeg, hypotenuse);
}
}以下哪些说法是正确的?
- [ ] The line marked
/*A*/is a problem for rep exposure because arrays are mutable. - [x]
/*B*/处有问题,因为这种表示方法会让使用者依赖于类型内部的表示。 - [ ] The line marked
*C*is a problem because creator operations should not have preconditions. - [ ] The two lines marked
/*D*/are a problem because they put legA, legB, and hypotenuse into the rep without doing a defensive copy first. - [x]
/*E*/处有问题,因为这影响到了类的不可变性。
表示不变量和抽象函数
我们现在深入理解一下抽象数据类型背后的理论,这些理论不仅本身很有趣,它们在ADT的设计与实现中也很有意义。如果你能够很好的理解它们,你将会设计出更好的抽象类型,并且远离那些隐晦的陷阱。
在研究抽象类型的时候,先思考一下两个值域之间的关系:
表示域(space of representation values)里面包含的是值具体的实现实体。在简单的情况下,一个抽象类型只需要实现为单个的对象,但是更常见的情况是使用一个很多对象的网络。
抽象域里面包含的则是类型设计时支持使用的值。这些值是由表示域“抽象/想象”出来的,也是使用者关注的。例如,一个无限整数对象的抽象域是整个整数域,但是它的实现域可能是一个由原始整数类型(有限)组成的数组实现的,而使用者只关注抽象域。
但是,实现者是非常“在意”表示域(和抽象域)的,因为实现者的责任就是实现表示域到抽象域的转换(映射)。
例如,我们选择用字符串来表示一个字符集合:
public class CharSet {
private String s;
...
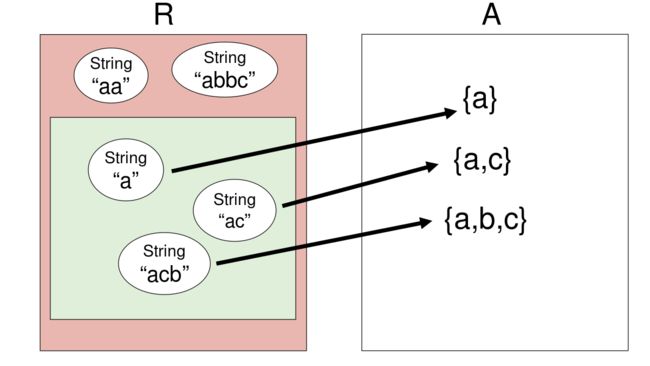
}如上图所示,表示域R包含的是我们的实现实体(字符串),而抽象域里面是抽象类型表示的字符集合,我们用箭头表示这两个域之间的映射关系。这里要注意几点:
- 每一个抽象值都是由表示值映射而来 。我们之前说过实现抽象类型的意义在于支持对于抽象值的操作,即我们需要能够创建和管理所有的抽象值,因此它们也必须是可表示的。
- 一些抽象值是被多个表示值映射而来的。这是因为表示方法并不是固定的,我们可以灵活的表示一个抽象值。
- 不是所有的表示值都能映射到抽象域中。在上面这个例子中,“abbc”就没有被映射。因为我们已经确定了表示值的字符串中不能含有重复的字符——这样我们的
remove方法就能在遇到第一个对应字符的时候停止,因为我们知道没有重复的字符。
由于我们不可能对每一个映射一一解释,为了描述这种对应关系和这两个域,我们再定义两个概念:
抽象函数abstraction function是表示值到其对应的抽象值的映射:
AF : R → A
快照图中的箭头表示的就是抽象函数,可以看出,这种映射是满射,但不一定是单射(不一定是双射)。
表示不变量rep invariant是表示值到布尔值的映射:
RI : R → boolean
对于表示值r,当且仅当r被AF映射到了A,RI(r)为真。换句话说,RI告诉了我们哪些表示值是“良好组织”的(能够去表示A中的抽象值),在下图中,绿色表示的就是RI(r)为真的部分,AF只在这个子集上有定义。
例如上图中,CharSet这种类型的实现禁止有重复字符,所以 RI(“a”) = true, RI(“ac”) = true, RI(“acb”) = true, 但是 RI(“aa”) = false, RI(“abbc”) = false.其中为假的集合用红色区域表示,合法的(为真)的字符串集合用绿色表示。
表示不变量和抽象函数都应该在表示声明后注释出来:
public class CharSet {
private String s;
// Rep invariant:
// s contains no repeated characters
// Abstraction function:
// AF(s) = {s[i] | 0 <= i < s.length()}
...
}一个常见的疑惑就是,抽象函数和表示不变量似乎是被表示域和抽象域决定的,甚至似乎抽象域就可以决定它。如果是这样的话,那么它们的定义似乎没什么用。
首先证明抽象域并不能独立决定AF和RI:对于同样的抽象类型可以有多种表示方法。例如对于一个字符集合,我们既可以用字符串来表示,也可以用比特向量来表示,每一个比特位对应一个可能的字符。显然我们需要两个不同的抽象函数来表示这两种不同的映射。
现在我们再来证明表示域和抽象域也不能决定AF和RI。这里的关键点在于,当我们确定表示域(表示值的空间)后,我们并不能决定哪一些表示值是合法的,以及如果它是合法的,它会被怎么解释/映射。例如在上面的例子中,我们也可以允许表示值有重复的字符,但是我们要求表示值中的字符必须是排好序的,因为这样我们就可以对其进行二分查找而非线性的遍历了。对于同一个表示域,我们得到了不同的表示不变量:
public class CharSet {
private String s;
// Rep invariant:
// s[0] <= s[1] <= ... <= s[s.length()-1]
// Abstraction function:
// AF(s) = {s[i] | 0 <= i < s.length()}
...
}最后,即使是同样的抽象域和表示域以及同样的表示不变量,我们也可能有不同的解释方法/抽象函数。还是上面的例子,我们可以对表示值中相邻的字符做不同的解释: "acgg" 被解释为[a-c] 和 [g-g]中的字符,即{a,b,c,g}。现在的映射如下图所示:
public class CharSet {
private String s;
// Rep invariant:
// s.length() is even
// s[0] <= s[1] <= ... <= s[s.length()-1]
// Abstraction function:
// AF(s) = union of { c | s[2i] <= c <= s[2i+1] }
// for all 0 <= i < s.length()/2
...
}总之,一个ADT的实现不仅是选择表示域(规格说明)和抽象域(具体实现),同时也要决定哪一些表示值是合法的(表示不变量),合法表示会被怎么解释/映射(抽象函数)。
所以,你必须像我们一样在代码中写出这些设计,以便别的程序员(或者未来的你)明白这些表示到底意味着什么。为什么呢?当程序员不明白表示的含义时会发生什么问题呢?请完成下面的阅读小练习。
你可以在Github上找到上面例子中
CharSet的三种实现的代码。
阅读小练习
Exploring a rep
请思考上面 CharSet 的最后一种实现方式:
public class CharSet {
private String s;
// Rep invariant:
// s.length() is even
// s[0] <= s[1] <= ... <= s[s.length()-1]
// Abstraction function:
// AF(s) = union of { c | s[2i] <= c <= s[2i+1] }
// for all 0 <= i < s.length()/2
...
}下面哪个选项的 s 满足了表示不变量?
[ ]
"abc"[x]
"abcd"[x]
"eeee"[x]
"ad"[ ]
"adad"[ ]
""(译者注:s.length()-1)
AF("acfg") 会映射到哪一个集合?
[ ] {a,b,c,d,e,f,g}
[x] {a,b,c,f,g}
[ ] {a,c,f,g}
[ ] some other abstract value
[ ] no abstract value, because
"acfg"does not satisfy the rep invariant
下面哪一个选项会和 "tv"映射到同一个抽象值?
[ ]
"ttv"[x]
"ttuuvv"[x]
"ttuv"[ ]
"tuv"
Who knows what?
以下哪一些选项是使用者需要了解的?
[x] 抽象域
[ ] 抽象函数
[x] 创建者
[x] 观察者
[ ] 表示域
[ ] 表示不变量
以下哪一些选项是开发者需要了解的?
- [x] 抽象域
- [x] 抽象函数
- [x] 创建者
- [x] 观察者
- [x] 表示域
- [x] 表示不变量
Rep invariant pieces
假设 C 这种抽象数据类型的表示用到了两个字符串:
class C {
private String s;
private String t;
...
}假设你不知道任何关于C抽象的信息,以下哪一些选项可能是C的表示不变量?
[x]
s只能包含字母[x]
s.length() == t.length()[ ]
srepresents a set of characters[ ]
C’s observers[x]
s是t反序过来的结果[ ]
s+t
Trying to implement without an AF/RI
假设Louis 是这样表示CharSet的:
public class CharSet {
private String s;
...
}不幸的是,Louis忘记写下抽象函数(AF)和表示不变量(RI)了。这里有四中可能的AF/RI对。它们在之前的例子中已经提到过了:
SortedRep:
// AF(s) = {s[i] | 0 <= i < s.length()}
// RI: s[0] < s[1] < ... < s[s.length()-1]SortedRangeRep:
// AF(s) = union of { c | s[2i] <= c <= s[2i+1] }
// for all 0 <= i < s.length()/2
// RI: s.length() is even, and s[0] <= s[1] <= ... <= s[s.length()-1]NoRepeatsRep:
// AF(s) = {s[i] | 0 <= i < s.length()}
// RI: s contains no character more than onceAnyRep:
// AF(s) = {s[i] | 0 <= i < s.length()}
// RI: true假设Louis有三个不同的朋友在帮助他分别实现该类型的三个操作: add(), remove(), and contains(),每一个朋友对这种类型的表示都有自己的猜想。
对于下面 add()的实现,哪一种AF/RI是可以对的上的?
/**
* Modifies this set by adding c to the set.
* @param c character to add
*/
public void add(char c) {
s = s + c;
}[ ] SortedRep
[ ] SortedRangeRep
[ ] NoRepeatsRep
[x] AnyRep
Trying to implement without an AF/RI #2
对于下面 remove()的实现,哪一种AF/RI是可以对的上的?
/**
* Modifies this set by removing c, if found.
* If c is not found in the set, has no effect.
* @param c character to remove
*/
public void remove(char c) {
int position = s.indexOf(c);
if (position >= 0) {
s = s.substring(0, position) + s.substring(position+1, s.length());
}
}[x] SortedRep
[ ] SortedRangeRep
[x] NoRepeatsRep
[ ] AnyRep
Trying to implement without an AF/RI #3
对于下面 contains()的实现,哪一种AF/RI是可以对的上的?
/**
* Test for membership.
* @param c a character
* @return true iff this set contains c
*/
public boolean contains(char c) {
for (int i = 0; i < s.length(); i += 2) {
char low = s.charAt(i);
char high = s.charAt(i+1);
if (low <= c && c <= high) {
return true;
}
}
return false;
}[ ] SortedRep
[x] SortedRangeRep
[ ] NoRepeatsRep
[ ] AnyRep
例子:有理数
这里列出了一个表示有理数的例子。仔细观察表示不变量和抽象函数。我们似乎可以允许更多的表示值是合法的,但是这样做会让一些操作的实现变得复杂(假设变了),另一些操作则可能变得简单。
public class RatNum {
private final int numerator;
private final int denominator;
// Rep invariant:
// denominator > 0
// numerator/denominator is in reduced form
// Abstraction function:
// AF(numerator, denominator) = numerator/denominator
/** Make a new RatNum == n.
* @param n value */
public RatNum(int n) {
numerator = n;
denominator = 1;
checkRep();
}
/** Make a new RatNum == (n / d).
* @param n numerator
* @param d denominator
* @throws ArithmeticException if d == 0 */
public RatNum(int n, int d) throws ArithmeticException {
// reduce ratio to lowest terms
int g = gcd(n, d);
n = n / g;
d = d / g;
// make denominator positive
if (d < 0) {
numerator = -n;
denominator = -d;
} else {
numerator = n;
denominator = d;
}
checkRep();
}
}阅读小练习
RatNum
阅读上面的代码和快照图,对于下面的每一种现象/属性,哪一行代码“负有最大的责任”(导致)?
RatNum(1,-2) 出现在 R的红色区域:
[ ]
private final int numerator;[ ]
private final int denominator;[ ]
// Rep invariant:[x]
// denominator > 0[ ]
// numerator/denominator is in reduced form[ ]
// Abstraction function:[ ]
// AF(numerator, denominator) = numerator/denominator
RatNum(2,4) 出现在 R的红色区域:
[ ]
private final int numerator;[ ]
private final int denominator;[ ]
// Rep invariant:[ ]
// denominator > 0[x]
// numerator/denominator is in reduced form[ ]
// Abstraction function:[ ]
// AF(numerator, denominator) = numerator/denominator
RatNum(-1,2)到 -1/2 有一个箭头:
[ ]
private final int numerator;[ ]
private final int denominator;[ ]
// Rep invariant:[ ]
// denominator > 0[ ]
// numerator/denominator is in reduced form[ ]
// Abstraction function:[x]
// AF(numerator, denominator) = numerator/denominator
检查表示不变量
表示不变量不仅是一个简洁的数学概念,你还可以通过断言检查它的不变属性来动态捕捉bug。例如上面的RatNum,这里就举出了一种检查的方法:
// Check that the rep invariant is true
// *** Warning: this does nothing unless you turn on assertion checking
// by passing -enableassertions to Java
private void checkRep() {
assert denominator > 0;
assert gcd(Math.abs(numerator), denominator) == 1;
}你应该在每一个创建或者改变表示数据的操作后调用 checkRep() 检查不变量,换句话说,就是在使用创建者、生产者以及改造者之后。在上面的RatNum中,你可以看到我们在两个创建者的最后都使用了 checkRep() 进行检查。
虽然说观察者通常不需要使用 checkRep() 进行检查,但这也是一个不错的主意。为什么?因为在每一个操作中调用 checkRep() 检查不变量更能够帮助你捕捉因为表示暴露而带来的bug。
为什么 checkRep() 是私有的?谁应该为为表示不变量负责?使用者还是实现者?
阅读小练习
Checking the rep invariant
以下哪一个选项的说法是正确的?
[ ]
checkRep()is the abstraction function[x]
checkRep()断言检查了表示不变量[x] 对于实现者来说,在每一个类的公共方法返回前调用
checkRep()进行检查是一个好主意[ ] it’s good for a client to call
checkRep()just after calling a public method of an ADT class
不要在表示中使用Null
回忆一下我们之前说过的使用null的坏处(译者注:“规格说明”),我们应该尽可能在编程中避免它。正因为如此,我们之前说如果没有特殊说明,前置条件和后置条件中都隐式包含不会有null值出现。
现在我们将这种闲置扩展到抽象数据类型的表示中。默认情况下,我们不允许表示中的索引出现null值(包括数组或者列表中的元素)。例如,如果你的表示是:
class CharSet {
String s;
}那么表示不变量中默认就会有 s != null ——你不需要专门在表示不变量的注释中进行说明。
然而,当你在实现检查表示不变量的 checkRep() 时,你应该显式的检查 s != null,确保当 s 是 null 的时候会快速失败。通常来说,这种检查会是自动的,因为很多操作在内容是null时会自动抛出异常,例如:
private void checkRep() {
assert s.length() % 2 == 0;
...
}这个时候你就不需要使用 assert s != null,因为对 s.length() 的调用会在s为null的时候自动失败报错。但是如果没有对null的自动检查,你就需要显式的使用 assert s != null了。
友善改动
回忆之前我们对于不可变类型的定义:对象一旦被创建其值不会发生更改。现在我们学习了抽象数据类型中的表示域和抽象域,我们可以将这个定义更加细化一下:对象一旦被创建,其抽象值不会发生改变。也就是说,对于使用者来说,其代表的值是不会变的,但是实现者可以在底层对表示域做一些改动,这些不会影响到抽象域的改动就称为友善改动(beneficent mutation).
这里举出了一个之前提到的RatNum类型,不过我们将表示不变量的限制放宽了,不再要求分子和分母必须是最简形式:
public class RatNum {
private int numerator;
private int denominator;
// Rep invariant:
// denominator != 0
// Abstraction function:
// AF(numerator, denominator) = numerator/denominator
/**
* Make a new RatNum == (n / d).
* @param n numerator
* @param d denominator
* @throws ArithmeticException if d == 0
*/
public RatNum(int n, int d) throws ArithmeticException {
if (d == 0) throw new ArithmeticException();
numerator = n;
denominator = d;
checkRep();
}
...
}这样的话,再显示值之前,我们要对其进行简化:
/**
* @return a string representation of this rational number
*/
@Override
public String toString() {
int g = gcd(numerator, denominator);
numerator /= g;
denominator /= g;
if (denominator < 0) {
numerator = -numerator;
denominator = -denominator;
}
checkRep();
return (denominator > 1) ? (numerator + "/" + denominator)
: (numerator + "");
}注意到 toString 实现更改了私有区域 numerator 和 denominator, 即它改变了表示域——虽然这还是一个观察者!但是关键点在于,这种改动并没有改变映射到的抽象值。我们对分子分母进行的约分和同乘-1的操作并没有改变AF(numerator, denominator) = numerator/denominator的行为。也可以这样想,AF是一种多对一函数,即一个表示值可以用多种表示值来实现。所以这种改动是无害的,也就是“友善”的。
我们会在后面的课程中看到很多使用友善改动的例子。这种实现上的自由通常可以带来性能上的提升,例如缓冲、数据结构再平衡、延迟清除等策略。
AF, RI以及表示暴露安全性的注解
你应该在抽象类型(私有的)表示声明后写上对于抽象函数和表示不变量的注解,这是一个好的实践要求。我们在上面的例子中也是这么做的。
当你在描述抽象函数和表示不变量的时候,注意要清晰明确:
- 对于RI(表示不变量),仅仅宽泛的说什么区域是合法的并不够,你还应该说明是什么使得它合法/不合法。
- 对于AF(抽象函数)来说,仅仅宽泛的说抽象域表示了什么并不够。抽象函数的作用是规定合法的表示值会如何被解释到抽象域。作为一个函数,我们应该清晰的知道从一个输入到一个输入是怎么对应的。
本门课程还要求你将表示暴露的安全性注释出来。这种注释应该说明表示的每一部分,它们为什么不会发生表示暴露,特别是处理的表示的参数输入和返回部分(这也是表示暴露发生的位置)。
下面是一个Tweet类的例子,它将表示不变量和抽象函数以及表示暴露的安全性注释了出来:
// Immutable type representing a tweet.
public class Tweet {
private final String author;
private final String text;
private final Date timestamp;
// Rep invariant:
// author is a Twitter username (a nonempty string of letters, digits, underscores)
// text.length <= 140
// Abstraction function:
// AF(author, text, timestamp) = a tweet posted by author, with content text,
// at time timestamp
// Safety from rep exposure:
// All fields are private;
// author and text are Strings, so are guaranteed immutable;
// timestamp is a mutable Date, so Tweet() constructor and getTimestamp()
// make defensive copies to avoid sharing the rep's Date object with clients.
// Operations (specs and method bodies omitted to save space)
public Tweet(String author, String text, Date timestamp) { ... }
public String getAuthor() { ... }
public String getText() { ... }
public Date getTimestamp() { ... }
}注意到我们并没有对 timestamp 的表示不变量进行要求(除了之前说过的默认 timestamp!=null)。但是我们依然需要对timestamp 的表示暴露的安全性进行说明,因为整个类型的不变性依赖于所有的成员变量的不变性。
下面是关于 RatNum的另一个例子:
// Immutable type representing a rational number.
public class RatNum {
private final int numerator;
private final int denominator;
// Rep invariant:
// denominator > 0
// numerator/denominator is in reduced form, i.e. gcd(|numerator|,denominator) = 1
// Abstraction function:
// AF(numerator, denominator) = numerator/denominator
// Safety from rep exposure:
// All fields are private, and all types in the rep are immutable.
// Operations (specs and method bodies omitted to save space)
public RatNum(int n) { ... }
public RatNum(int n, int d) throws ArithmeticException { ... }
...
}可以看到,对于不可变类型的表示,表示暴露的安全性说明会简单很多。
你可以在GitHub获取
RatNum的所有代码
阅读小练习
Arguing against rep exposure
思考这个抽象数据类型:
// Mutable type representing Twitter users' followers.
public class FollowGraph {
private final Map> followersOf;
// Rep invariant:
// all Strings in followersOf are Twitter usernames
// (i.e., nonempty strings of letters, digits, underscores)
// no user follows themselves, i.e. x is not in followersOf.get(x)
// Abstraction function:
// AF(followersOf) = the follower graph where Twitter user x is followed by user y
// if and only if followersOf.get(x).contains(y)
// Safety from rep exposure:
// All fields are private, and ..???..
// Operations (specs and method bodies omitted to save space)
public FollowGraph() { ... }
public void addFollower(String user, String follower) { ... }
public void removeFollower(String user, String follower) { ... }
public Set getFollowers(String user) { ... }
} 对于上面代码中的注解,下面哪一个选项可以正确的替代 ..???.. ,从而使得表示暴露的安全性得到说明?
1. “Strings are immutable.”
No
2. “followersOf 是一个可变的 Map, 其包含着可变的 Set 对象,但是 getFollowers() 在返回时会对 Set 进行防御性复制,并且其他的参数和返回值都是不可变类型的 String 或者 void .”
Yes
3. “This class is mutable, so rep exposure isn’t an issue.”
No
4. “followersOf is a mutable Map, but it is never passed or returned from an operation.”
No
5. “FollowGraph() does not expose the rep; addFollower() does not expose the rep; removeFollower() does not expose the rep; getFollowers() does not expose the rep.”
No
6. “String 是不可变的, 并且表示中的 Set 对象都使用了不可变包装。虽然Map类型是可变的,但是没有操作传入或者返回这种类型的对象。”
Yes
一个ADT的规格说明应该写什么?
由于我们已经讲了如何对表示不变量和抽象函数做注解,现在我们就来更新一下我们对于规格说明的理解,即一个ADT的规格说明应该写什么?
如上图所示,规格说明在使用者和实现者之间构建起了一道“防火墙”。抽象类型的规格说明(包含操作的说明)应该只关注使用者可见的部分,这包括参数、返回值、可能抛出的异常。例如规格说明需要引用T的值时,它应该是抽象域的值而非表示域。
规格说明不应该谈论具体的表示/实现细节,例如表示域里面的值。它应该认为表示本身(私有区域)对于使用者是不可见的,就像是方法里面的局部变量对外部不可见。这也是为什么我们在注解表示不变量和抽象函数的时候使用的是"\\"注释而非典型的Javadoc格式。如果我们使用Javadoc注释的话,内部的实现细节会出现在规格说明中,而这会影响表示独立性以及信息隐藏。
用ADT不变量替换前置条件
良好设计的ADT的一个大优点在于我们可以使用它将本该写在前置条件中的限制封装起来。例如,现在有一个规格说明是这样:
/**
* @param set1 is a sorted set of characters with no repeats
* @param set2 is likewise
* @return characters that appear in one set but not the other,
* in sorted order with no repeats
*/
static String exclusiveOr(String set1, String set2);我们可以利用ADT(SortedSet)的不变量属性要求这种前置条件:
/** @return characters that appear in one set but not the other */
static SortedSet exclusiveOr(SortedSet set1, SortedSet set2); 这满足了我们所有的要求:
- 远离bug:因为要求的条件(排序、无重复)都已经是ADT的不变量了,所以Java可以对其进行静态检查,在编译期阻止所有不满足的操作。
- 易于理解:因为这样写更简单,并且ADT
SortedSet的名字就已经表明了它该有的属性。 - 可改动:因为我们可以改变
SortedSet的内部实现而不影响exclusiveOr或其他的使用者代码。
我们以前很多用前置条件的地方现在都可以用定制的ADT来替换。
阅读小练习
Encapsulating preconditions in ADTs
思考下面这个方法:
/**
* Find tweets written by a particular user.
*
* @param tweets a list of tweets with distinct timestamps, not modified by this method.
* @param username Twitter username (a nonempty sequence of letters, digits, and underscore)
* @return all and only the tweets in the list whose author is username,
* in the same order as in the input list.
*/
public static List writtenBy(List tweets, String username) { ... } 你会创建一个什么ADT来避开这种繁杂的前置要求?
[ ]
TweetsAndUsername[x]
TweetList[x]
Username[ ]
UsernameCharacter
如何建立不变量
不变量是一种在程序中一直为真的属性,对于对象而言,就是从对象创建开始一直具有的属性。
为了保持一个不变量,我们需要:
- 确保在对象创建的时候不变量成立
- 确保对对象在接下来的每一个改变后不变量依然成立
- 译者注:这就是状态机中的不变性 状态机:如何构建稳定的婚姻
翻译成对于ADT的操作,就是:
- 创建者和生产者必须对新的对象就建立不变量
- 改造者和观察者必须保持/保护这种不变量
表示暴露会使得情况更加复杂,如果一个表示被暴露出来,那么程序的任何地方都可能对其进行修改,我们也就没法确保不变量一直成立了。所以使用不变量完整的规则应该是:
结构归纳法. 如果一个抽象数据类型的不变量满足:
- 被创建者或生产者创建;
- 被改造者和观察者保持;
- 没有表示暴露。
那么这种类型的所有实例的不变量都是成立的。
阅读小练习
Structural induction
Recall this data type from the first exercise in this reading:回忆在第一个练习中的数据类型:
/** Represents an immutable right triangle. */
class RightTriangle {
private double[] sides;
// RI: ???
// AF: ???
// sides[0] and sides[1] are the two legs,
// and sides[2] is the hypotenuse, so declare it to avoid having a
// magic number in the code:
public static final int HYPOTENUSE = 2;
/** Make a right triangle.
* @param legA, legB the two legs of the triangle
* @param hypotenuse the hypotenuse of the triangle.
* Requires hypotenuse^2 = legA^2 + legB^2
* (within the error tolerance of double arithmetic)
*/
public RightTriangle(double legA, double legB, double hypotenuse) {
this.sides = new double[] { legA, legB, hypotenuse };
}
/** Get all the sides of the triangle.
* @return three-element array with the triangle's side lengths
*/
public double[] getAllSides() {
return sides;
}
/** @return length of the triangle's hypotenuse */
public double getHypotenuse() {
return sides[HYPOTENUSE];
}
/** @param factor to multiply the sides by
* @return a triangle made from this triangle by
* multiplying all side lengths by factor.
*/
public RightTriangle scale(double factor) {
return new RightTriangle (sides[0]*factor, sides[1]*factor, sides[2]*factor);
}
/** @return a regular triangle made from this triangle.
* A regular right triangle is one in which
* both legs have the same length.
*/
public RightTriangle regularize() {
double bigLeg = Math.max(sides[0], sides[1]);
return new RightTriangle (bigLeg, bigLeg, sides[2]);
}
}这个数据类型中有一个重要的不变量,那就是直角边和斜边之间的勾股关系。
假设使用者遵守了规格说明,以下哪一个说法是正确的?
[x] 创建者
RightTriangle()建立的不变量- [ ] The observer
getAllSides()preserves the invariant - [x] 观察者
getHypotenuse()保持了不变量 - [x] 生产者
scale()保持了不变量 [ ] The producer
regularize()preserves the invariant
总结
- 不变量是指对于一个对象,它有一种能够在整个生命周期保证为真的属性。
- 一个好的ADT会确保它的不变量为真。不变量是由创建者和生产者创建,被观察者和改造者保持。
- 表示不变量明确了什么是合法的表示值,并且这些表示应该在运行时调用
checkRep()检查。 - 抽象函数将具体的表示映射到抽象值上。
- 表示暴露会威胁到表示独立性和表示不变量。
下面将这篇阅读的知识点与我们的三个目标联系起来:
- 远离bug. 一个好的ADT会确保它的不变量为真,因此它们不会被使用者代码中的bug所影响。同时,通过显式的声明和动态检查不变量,我们可以尽早的发现bug,而不是让错误的行为继续下去。
- 易于理解. 表示不变量和抽象函数详细的表述了抽象类型中表示的意义,以及它们是如何联系到抽象值的。
- 可改动. 抽象数据类型分离了抽象域和表示域,这使得实现者可以改动具体实现而不影响使用者的代码。