红黑树完全攻略
文章目录
- 1. 前言
- 2. 旋转
- 2.1 为什么旋转
- 2.2 基础旋转
- 2.3 复杂旋转
- 3. 红黑树的性质
- 4. 插入
- 4.1 插入论证
- 4.2 复杂插入
- 4.2.1 U 为红色的场景
- 4.2.2 U 为黑色的场景
- 4.3 复杂插入总结
- 5. 删除
- 5.1 删除问题转化
- 5.2 删除情况枚举
- 5.3 复杂删除
- 5.3.1 N 有个红色的兄弟 U
- 5.3.2 N 有个黑色兄弟 U
- 5.3.3 N 有个黑色兄弟 U 续
- 5.3.4 N 有个黑色的兄弟 U 续续
- 5.3 复杂删除总结
- 6. 实现
- 6.1 如何测试
- 7. 参考资料
1. 前言
这次重新看《后会无期》的时候，反复思考了「听过很多道理，依然过不好这一生」这句话的正确性。反复思考的问题有三个：
-
道理是否适用于自己？ —> 道理是所有通用场景下，抽象出来的共性，不具有个体特征。
-
什么场景下道理是成立的？—> 道理成立的场景是什么。
-
如何定义好的标准？ —> thinking
注：「一分耕耘一分收获」只有在绝对理想的情况下才能成立，在气候、价格有任何波动的情况下都不会完美的呈现正比例关系。
2. 旋转
为什么要写个前言 ，是因为笔者突然意识到思考是比做更重要的事情。99% 写红黑树文章介绍的，都告诉你要做旋转，要左旋、要右旋。但请记得所有不告诉你理由，但是要求必须这么做的都是在「耍流氓」。
2.1 为什么旋转
问：红黑树是一种什么树？
答：平衡二叉搜索树，提取定语平衡 、二叉搜索树 。
- 二叉搜索树：左孩子比根小，右孩子比根大，详情请戳链接。
- 平衡二叉搜索树：在满足二叉搜索树性质的基础上增加叶结点的高度差不超过 1 的限制，详情请戳链接。
2.2 基础旋转
假设现在只存在三个节点，插入可选方式如下：
- 根 -> 左 -> 右 （未违反平衡的性质）
- 根 -> 左 -> 左、根 -> 左 -> 右、根 -> 右 -> 右、根 -> 右 -> 左 （ 违反平衡性质）
违反性质的四种情况如下图所示，在满足平衡二叉搜索树的性质的情况下，只有两种旋转是合法的：
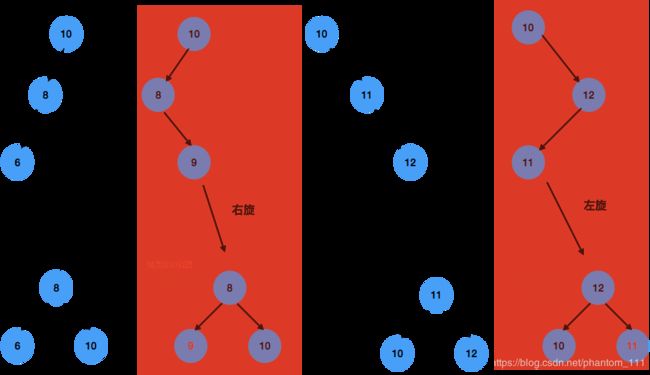
问：如何将不合法的旋转变的合法化呢？
既然只有 根 -> 左 -> 左、根 -> 右 -> 右 这两种情况可以做旋转，那么先定两个小目标：
- 将 根 -> 左 -> 右 变成 根 -> 左 -> 左
- 左旋可解：根的右孩子变为根，根的变为根的左孩子
- 将 根 -> 右 -> 左 变成 根 -> 右 -> 右
- 右旋可解：根的左孩子变成根，根变成根的右孩子
进行上述步骤的调整后，所有情况都变为可做旋转的两种情况，然后继续旋转就好啦。
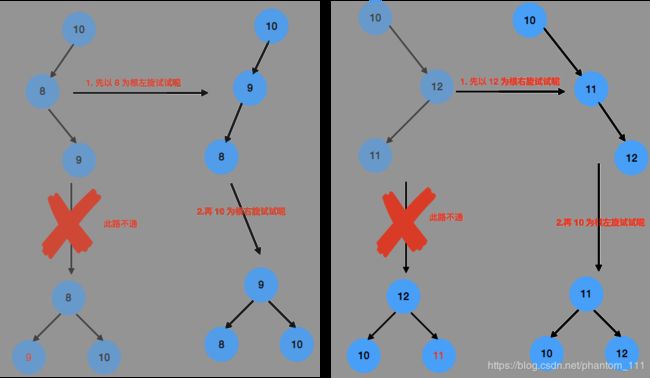
喜大普奔，现在所有可枚举的插入情况，均能够平衡化。
2.3 复杂旋转
上面的基础旋转是所有节点只存在一个孩子的情况，那如果有两个孩子要怎么旋转呢？
这里其实不必死记硬背，记住「出来混迟早要还的」就好。以右旋为例：
- 根 10 会变成左孩子 8 的右孩子，那么根 10 的左孩子现在处于缺失状态
- 左孩子 8 的右孩子会变成根 10 ，那么跟 8 的右孩子 9 会处于游离状态
- 咦，这里直接把游离的右孩子 9 跟变为根 10 的左孩子，一起就又会恢复平静了
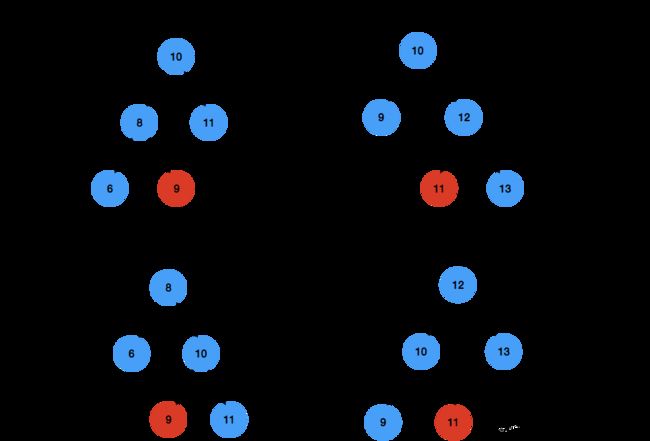
3. 红黑树的性质
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色（叶子是NIL节点）。
- 从每个叶子到根的所有路径上不能有两个连续的红色节点。
- 从任一节点到其每个叶子的所有不包含重复点的路径都包含相同数目的黑色节点。
注：
请读 10 遍，然后死记硬背下来（ps 人家就是这么规定的，我也不知道为啥？就好像 red 和 black 为啥这么拼写一样……
红黑树并没有要求绝对的平衡性
4. 插入
敲黑板划重点，虽然性质是人家规定的，但是想法是自己的不是。
请不要先想任何性质上的规则，要想下现在面临的问题：
- 每次插入的节点是红色好还是黑色好呢？
-
做为一个成熟的年轻人，我猜你一定会选红色，为什么呢？因为黑色的话，你每插入一个节点都会违反性质 5 ，也就意味着你每次都必须做旋转。
注：看了这么久，思考个问题吧 —— 你说是木棍打头痛，还是铁棍打头痛呢？（ps 单纯皮一下，因为我盲猜你一定困了……
- 先想下插入的可枚举情况有：
- 插入根节点 : 置该节点为黑色，无需调整
- 插入非根节点：
- 该节点的父亲是黑色，无需调整
- 该节点的父亲是红色，需要调整，那怎么调整呢？
- 简单将父亲节点置为黑色可以嘛（ ps 太傻太天真，人家可是红黑树啊，怎么会这么简单呢……
4.1 插入论证
上述两种简单的插入情况，笔者就不写了，我确信以及相信你们肯定都能理解清楚。
先看下 too young too simple too naive 的想法为什么不行，毕竟笔者是个讲道理的人。
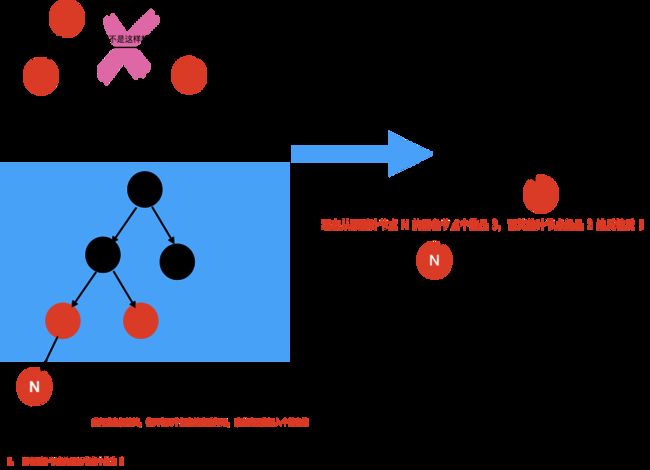
让我们先想一想矛盾点是什么
-
为了满足性质 4 ，需要将插入节点的父节点置为黑色，但能推导出来的结论是：
- 所有以该父节点为根的子树仍满足红黑树性质
- 所有从根节点经过该父节点的路径，黑色节点个数都会加 1，造成违反性质 5
注： 这段有点绕，但其实就是上图的翻译，理解不清楚的话可以看图多想一会会
划重点了，在红红是父子关系的时候，我们不能随意的将父节点置为黑色，即不能随意将某条路径上黑色节点的个数加 1 ，要秉承着「一荣俱荣，一损俱损」的观点，翻译过来就是：
- 左边黑节点个数加 1 可以，右边你也得给我加 1
- 左边黑节点个数减 1 可以，右边你也得给我减 1
4.2 复杂插入
知易行难，所以该怎么做的呢？别急，让我们在思考下，我们现在能够判断出来的内容：
- N 和父亲 P 均为红色，在红红不为父子的限制下，N 的祖父一定为黑色
- N 的叔叔 U 可红色可黑色
又到了枚举情况的环节，所有可列举情况如下
4.2.1 U 为红色的场景
核心将祖父节点 G 的颜色跟他的孩子 P 、U 颜色互换。
注： 这里设置 G 为红色，需判断 G 的父亲是否为红色，若是，则需要递归跳转，若否，则整棵树满足性质。
4.2.2 U 为黑色的场景
4.2.2.1 插入节点 N 在 P 的左边（符合可右旋的条件）
思考：为什么步骤 2 是右旋而不是将 G 节点的父亲置为黑色呢？
- 笔者认为原因有两个：
- 设置一个节点为黑色，必定会违反性质 5 ，导致整棵树都要做旋转。
- 父子节点交换颜色后，右旋就可以直接使得该子树满足红黑性质，不必对整棵树旋转。
4.2.2.2 插入的节点 N 在 P 的右边（不符合右旋条件）
没有条件也要创造条件，办法总比困难多
- 先左旋，为后面的右旋打基础 —> 转化为 4.2.2.1 的情况
- 交换父子颜色 + 右旋，所有性质都满足啦
4.3 复杂插入总结
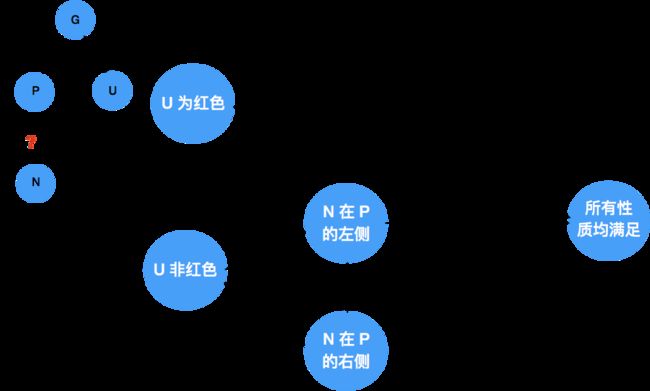
注： 在 U 为非红色，以及插入节点 N 在 P 节点右侧的情况下是最复杂的，如果没看懂怎么办呢？亲亲，这边建议您多看两遍哟……
5. 删除
絮絮叨叨的笔者终于把插入写完了，但是明显删除才是更难的啊，那咋办呢？
不妨不妨，来日方长，你以为我要收尾了吧，其实我主要就是想写下「不妨不妨，来日方长」这句话。（ps 没办法，就是这么皮呀
5.1 删除问题转化
枚举大法是真香呀！
-
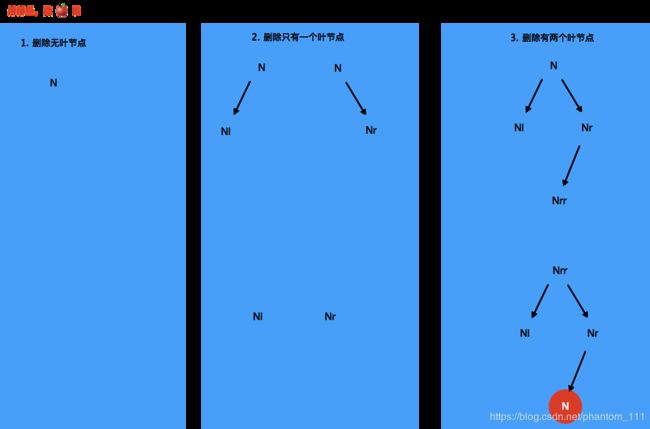
删除无孩子节点 —— 直接删除不用多想
-
删除只有一个孩子节点 —— 用孩子替代删除节点
-
删除有两个孩子节点
- 找到它右子树最小节点 M
- 将 M 值与待删除节点替换
- 删除 M
注：
M 一定只有一个孩子，因为他是右子树最小的节点啊，所以 M 的右孩子一定指向哨兵节点
替代节点 M 也可以是左子树最大的节点，并且也会只有一个孩子
结论： 问题转化为如何删除没有孩子的节点或者是删除只有一个孩子的节点啦。
5.2 删除情况枚举
删除在加上颜色限制以后的可枚举情况：
-
删除节点为红色 — 不违反任何红黑树性质，直接删除即可
-
删除节点为黑色
-
删除的黑色节点有一个红色的孩子 — 用他的孩子替代他，然后将孩子的颜色置为黑色
-
删除的黑色节点有一个黑色的孩子—讲真这是最不想看到的情况，照例单独讨论吧，因为真的太复杂了，笔者已经哭晕了……
注： 这么想要了解的知识，怎么可能知道一半就放弃呢……
5.3 复杂删除
删除黑色节点，本质就是造成某条路径上黑色节点的个数少 1 ，导致红黑树不再满足性质 5。来，别慌，跟我再复习一次。结点删除要秉承着「一荣俱荣，一损俱损」的观点，翻译过来就是：
- 左边黑节点个数加 1 可以，右边你也得给我加 1
- 左边黑节点个数减 1 可以，右边你也得给我减 1
鉴于笔者写到此处时脑子已经一团浆糊（其实是我自己构造不出来，想象中的场景），以下所有的删除都是局部视图，并且均已完成删除节点替换的步骤
5.3.1 N 有个红色的兄弟 U
5.3.2 N 有个黑色兄弟 U
黑色的兄弟 U 是个好兄弟，因为不仅他自己是黑色的，他的两个儿子也都是黑色的，笔芯。
注：U 置为红色后可能会违反红红不为父子的情况，若父节点 P 非红色，树满足性质；若父节点 P 为红色，递归调整。
5.3.3 N 有个黑色兄弟 U 续
黑色的兄弟 U 还蛮省心的因为他有个还算乖巧、不调皮捣蛋的儿子。
等等，先枚举下 U 儿子的可能性？
-
黑黑— 上面已经讨论过啦，写太多弊端就是读到下面会忘记上面，记不住的话我们回去复习复习呗 -
红红 — U 的左儿子 Ul 是个乖儿子，因为它是红色的
-
红黑 — U 的左儿子 Ul 是个乖儿子，因为它是红色的
-
黑红 — 这两个是个不省心的儿子，我们后面再继续讨论
5.3.4 N 有个黑色的兄弟 U 续续
醒醒，我们就快结束了，喝完这一杯，没有下一杯了……，所以亲亲，这边建议你戒骄戒躁，耐心看完呦！
复习下现在的场景，黑色的兄弟 U 有一对不省心的儿子，左儿子 Ul 是黑色，右儿子 Ur 红色。
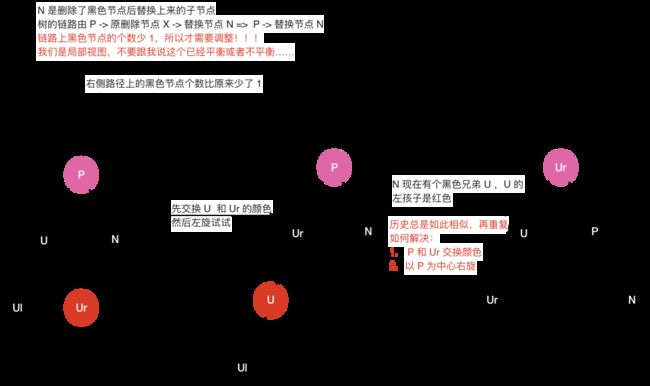
5.3 复杂删除总结
鉴于笔者脑子已经一团浆糊 + 非常困，复杂删除的总结图，我们就简单一点画好啦。
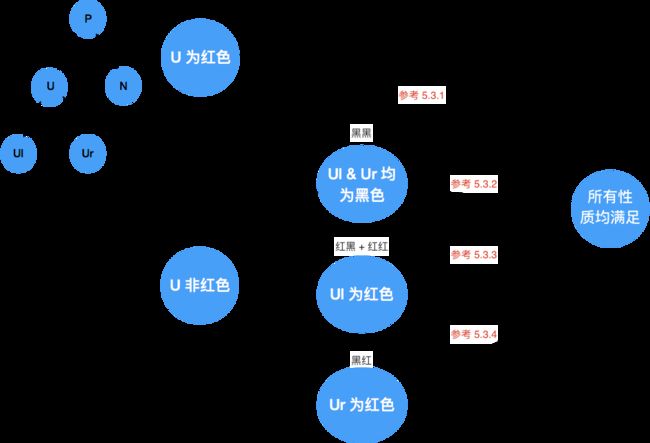
6. 实现
昔日战国七雄争霸，秦于长平之战斩杀赵军约 45 万。而此战失败的主要原因是，赵王遂弃用名将廉颇，而起用赵括代替廉颇，而赵括只会熟读兵书，但缺乏战场经验，不懂得灵活应变。
为什么写上面这段呢？可能是要反思自己不能只看书，不思考，不实现吧（ps 毕竟我是个天马行空的笔者……。
原则上讲，也不是我实现的，是我理解了思想后照抄了 nginx 的 rbtree 实现的源码。实现思路完全按照上述介绍的步骤。
go 实现的源码地址
注：笔者忙着总结文章，这里的代码有很多细节还木有打磨好，各位大侠请轻喷啊
6.1 如何测试
「有东西让你抄就很简单了」，复杂的是怎么确认自己抄的是否正确呢？
- 笔者大概看了下其他人红黑树的测试，大概都是单纯的测试下插入+ 先序遍历结果，总觉得不是很符合预期
- 后来想了下，测试其实应该测试各种插入、删除后是否仍满足红黑树的性质 (ps 不能吐槽我……)
7. 参考资料
-
维基百科红黑树
-
红黑树动态展示的网站
-
nginx 源码 src/core 目录下的 ngx_rbtree.h + ngx_rbtree.c —> 可自己拉源码看