non-local Means(非局部均值)降噪算法及快速算法原理与实现
Non-Local Means算法原理：
Non-Local Means顾名思义，这是一种非局部平均算法。何为局部平均滤波算法呢？那是在一个目标像素周围区域平滑取均值的方法，所以非局部均值滤波就意味着它使用图像中的所有像素，这些像素根据某种相似度进行加权平均。滤波后图像清晰度高，而且不丢失细节。非局部均值滤波由Baudes提出，其出发点应该是借鉴了越多幅图像加权的效果越好的现象，那么在同一幅图像中对具有相同性质的区域进行分类并加权平均得到去噪后的图片，应该降噪效果也会越好。该算法使用自然图像中普遍存在的冗余信息来去噪声。与双线性滤波、中值滤波等利用图像局部信息来滤波不同，它利用了整幅图像进行去噪。即以图像块为单位在图像中寻找相似区域，再对这些区域取平均，较好地滤除图像中的高斯噪声。NL-Means的滤波过程可以用下面公式来表示：
w代表权重。衡量相似度的方法有很多，最常用的是根据两个像素亮度差值的平方来估计。由于有噪声，单独的一个像素并不可靠，所以使用它们的邻域，只有邻域相似度高才能说这两个像素的相似度高。衡量两个图像块的相似度最常用的方法是计算他们之间的欧氏距离：
如上图所示，p为去噪的点，q1和q2的邻域与p相似，所以权重w(p,q1) 和w(p,q2) 较大，而邻域相差比较大的点q3的权重值w(p,q3) 很小。如果用一幅图把所有点的权重表示出来，那就得到下面这些权重图：
一般而言，考虑到算法复杂度，搜索区域大概取21x21，相似度比较的块的可以取7x7。实际中，常常需要根据噪声来选取合适的参数。当高斯噪声的标准差σ 越大时，为了提高算法鲁棒性，需要增大块区域，同样也需要增加搜索区域。同时，滤波系数h 与 σ 满足正相关：h=kσ，当块变大时，k 需要适当减小。
Non-Local Means算法实现：
function [output]=NLmeansfilter(input,t,f,h)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% input: image to be filtered
% t: radio of search window
% f: radio of similarity window
% h: degree of filtering
%
% Author: Jose Vicente Manjon Herrera & Antoni Buades
% Date: 09-03-2006
%
% Implementation of the Non local filter proposed for A. Buades, B. Coll and J.M. Morel in
% "A non-local algorithm for image denoising"
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Size of the image
[m n]=size(input);
% Memory for the output
Output=zeros(m,n);
% Replicate the boundaries of the input image
input2 = padarray(input,[f f],'symmetric');
% Used kernel
kernel = make_kernel(f);
kernel = kernel / sum(sum(kernel));
h=h*h;
for i=1:m
for j=1:n
i1 = i+ f;
j1 = j+ f;
W1= input2(i1-f:i1+f , j1-f:j1+f);
wmax=0;
average=0;
sweight=0;
rmin = max(i1-t,f+1);
rmax = min(i1+t,m+f);
smin = max(j1-t,f+1);
smax = min(j1+t,n+f);
for r=rmin:1:rmax
for s=smin:1:smax
if(r==i1 && s==j1) continue; end;
W2= input2(r-f:r+f , s-f:s+f);
d = sum(sum(kernel.*(W1-W2).*(W1-W2)));
w=exp(-d/h);
if w>wmax
wmax=w;
end
sweight = sweight + w;
average = average + w*input2(r,s);
end
end
average = average + wmax*input2(i1,j1);
sweight = sweight + wmax;
if sweight > 0
output(i,j) = average / sweight;
else
output(i,j) = input(i,j);
end
end
end
function [kernel] = make_kernel(f)
kernel=zeros(2*f+1,2*f+1);
for d=1:f
value= 1 / (2*d+1)^2 ;
for i=-d:d
for j=-d:d
kernel(f+1-i,f+1-j)= kernel(f+1-i,f+1-j) + value ;
end
end
end
kernel = kernel ./ f; 下面是我写的测试函数：
%% 测试函数
clc,clear all,close all;
ima=double(imread('3.jpg'));
[wid,len,channels]=size(ima);
% add noise
sigma=10;
rima=ima+sigma*randn(size(ima));
% denoise
fima=rima;
if channels>2
fori=1:channels
fima(:,:,i)=NLmeansfilter(rima(:,:,i),5,2,sigma);
end
end
% show results
subplot(1,3,1),imshow(uint8(ima)),title('original');
subplot(1,3,2),imshow(uint8(rima)),title('noisy');
subplot(1,3,3),imshow(uint8(fima)),title('filtered');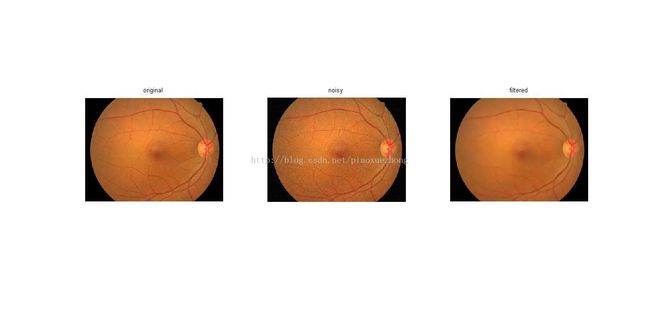
由于原始算法的复杂度较高，导致算法耗时及较长，所以针对NLM算法产生了不少优化算法，如使用积分图像技术对算法进行加速。为了降低空间复杂度，将偏移量作为最外层循环，即每次只需要在一个偏移方向上求取积分图像，并对该积分图像进行处理。而不需要一次性求取出所有积分图像，参考【6】。算法流程见下图：
先构造一个关于像素差值的积分图像：
其中
这样在计算两个邻域
和 
间的距离时，就可以在常量时间内完成：
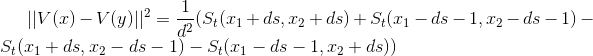
这样，整个算法复杂度将降为
。具体代码如下：
function DenoisedImg=fastNLmeans(I,ds,Ds,h)
%I:含噪声图像
%ds:邻域窗口半径
%Ds:搜索窗口半径
%h:高斯函数平滑参数
%DenoisedImg：去噪图像
I=double(I);
[m,n]=size(I);
PaddedImg = padarray(I,[Ds+ds+1,Ds+ds+1],'symmetric','both');
PaddedV = padarray(I,[Ds,Ds],'symmetric','both');
average=zeros(m,n);
sweight=average;
wmax=average;
h2=h*h;
d2=(2*ds+1)^2;
for t1=-Ds:Ds
for t2=-Ds:Ds
if(t1==0&&t2==0)
continue;
end
St=integralImgSqDiff(PaddedImg,Ds,t1,t2);
v = PaddedV(1+Ds+t1:end-Ds+t1,1+Ds+t2:end-Ds+t2);
w=zeros(m,n);
for i=1:m
for j=1:n
i1=i+ds+1;
j1=j+ds+1;
Dist2=St(i1+ds,j1+ds)+St(i1-ds-1,j1-ds-1)-St(i1+ds,j1-ds-1)-St(i1-ds-1,j1+ds);
Dist2=Dist2/d2;
w(i,j)=exp(-Dist2/h2);
sweight(i,j)=sweight(i,j)+w(i,j);
average(i,j)=average(i,j)+w(i,j)*v(i,j);
end
end
wmax=max(wmax,w);
end
end
average=average+wmax.*I;
sweight=sweight+wmax;
DenoisedImg=average./sweight;
function Sd = integralImgSqDiff(PaddedImg,Ds,t1,t2)
%PaddedImg：边缘填充后的图像
%Ds:搜索窗口半径
%(t1,t2):偏移量
%Sd:积分图像
[m,n]=size(PaddedImg);
m1=m-2*Ds;
n1=n-2*Ds;
Sd=zeros(m1,n1);
Dist2=(PaddedImg(1+Ds:end-Ds,1+Ds:end-Ds)-PaddedImg(1+Ds+t1:end-Ds+t1,1+Ds+t2:end-Ds+t2)).^2;
for i=1:m1
for j=1:n1
if i==1 && j==1
Sd(i,j)=Dist2(i,j);
elseif i==1 && j~=1
Sd(i,j)=Sd(i,j-1)+Dist2(i,j);
elseif i~=1 && j==1
Sd(i,j)=Sd(i-1,j)+Dist2(i,j);
else
Sd(i,j)=Dist2(i,j)+Sd(i-1,j)+Sd(i,j-1)-Sd(i-1,j-1);
end
end
end
function DenoisedImg=fastNLmeans2(I,ds,Ds,h)
I=double(I);
[m,n]=size(I);
PaddedImg = padarray(I,[Ds+ds+1,Ds+ds+1],'symmetric','both');
PaddedV = padarray(I,[Ds,Ds],'symmetric','both');
average=zeros(m,n);
wmax=average;
sweight=average;
h2=h*h;
d=(2*ds+1)^2;
for t1=-Ds:Ds
for t2=-Ds:Ds
if(t1==0&&t2==0)
continue;
end
Sd=integralImgSqDiff(PaddedImg,Ds,t1,t2);
SqDist2=Sd(2*ds+2:end-1,2*ds+2:end-1)+Sd(1:end-2*ds-2,1:end-2*ds-2)...
-Sd(2*ds+2:end-1,1:end-2*ds-2)-Sd(1:end-2*ds-2,2*ds+2:end-1);
SqDist2=SqDist2/d;
w=exp(-SqDist2/h2);
v = PaddedV(1+Ds+t1:end-Ds+t1,1+Ds+t2:end-Ds+t2);
average=average+w.*v;
wmax=max(wmax,w);
sweight=sweight+w;
end
end
average=average+wmax.*I;
average=average./(wmax+sweight);
DenoisedImg = average;
function Sd = integralImgSqDiff(PaddedImg,Ds,t1,t2)
Dist2=(PaddedImg(1+Ds:end-Ds,1+Ds:end-Ds)-PaddedImg(1+Ds+t1:end-Ds+t1,1+Ds+t2:end-Ds+t2)).^2;
Sd = cumsum(Dist2,1);
Sd = cumsum(Sd,2);测试结果如下：
参考：
- 《a non-local algorithm for image denoising》[J].IEEE
- https://en.wikipedia.org/wiki/Non-local_means
- http://wenhuix.github.io/research/denoise.html
- http://blog.csdn.net/piaoxuezhong/article/details/78317861
- http://blog.csdn.net/tuyang120428941/article/details/7052487
- http://blog.csdn.net/u010839382/article/details/48241929