海量数据挖掘MMDS week7: 局部敏感哈希LSH（进阶）

http://blog.csdn.net/pipisorry/article/details/48882167

海量数据挖掘Mining Massive Datasets(MMDs) -Jure Leskovec courses学习笔记 相似项的发现：局部敏感哈希(LSH, Locality-Sensitive Hashing)

{博客内容：More about Locality-Sensitive Hashing:在海量数据挖掘MMDS week2: 局部敏感哈希Locality-Sensitive Hashing, LSH中讲到的bands方法实际上只是一个特例，bands方法可以通过and-or级联实现，多个级联当然就是之前方法的拓展。The "bands" technique for LSH that we learned in Week 2 is actually just a special case of a more general technique.   We will look at a completely different approach to LSH, which is preferable when we are looking for sets of very high Jaccard similarity.}

局部敏感哈希函数族LSH families

{在海量数据挖掘MMDS week2: 局部敏感哈希Locality-Sensitive Hashing, LSH中，我们讨论了最小哈希函数minhash，接下来要讨论其它的LSH函数族，这些函数族也能高效地产生候选pairs，并能作用于集合空间和jaccard距离。下面要讲的就是面向jaccard距离的LSH函数族。}

LSH families的定义

定义一个判定函数f，判定两个输入是否是候选对。一般函数f对两个输入求hash值，hash值相同就说明是一个候选对。

这种形式的一系列函数集合构成一个函数族。如hash函数中的每个函数都基于特征矩阵的一个可能 的行排列转换而形成，这些函数构成一个函数族。

(d1,d2,p1,p2)-敏感的函数族的定义

 

例如minhash funcs假设点空间是集合sets，距离是Jaccard距离。

这里要注意的是，我们想要d1,d2固定的同时尽量分开p1,p2。

LSH哈希函数应满足的条件

最小哈希函数族minhash func families

minhash函数族实例

这里相等的概率就是1-距离。

局部敏感哈希族的放大amplify处理

{这就是要讨论hash函数族的目的，可以使概率p1变大，p2变小。lz觉得这里是通过AND和OR操作来控制之前文章讲到的S曲线。通过特例：and-or就可以模拟实现将signature矩阵划分成b个bands，每个bands有r行，同样得到S曲线f(S) = (1-S^r)^b的效果。如果通过多个级联会得到更优更复杂更接近阶跃函数的S曲线。}

hash函数的and构造

也就是说，F’中某个hash函数判定x,y候选对，实际上使用了r个hash函数来判定，r个hash函数都判定成功才成功，成功的概率当然会变成p^r。

hash函数的or构造

And和or构造的效果

AND construction like “rows in a band.”OR construction like “many bands.”

与构造中选取r要足够大，这样p2才会非常接近于0，同时p1也仍显著偏离0（注意这里并不是更接近于1了）。

也就量说这样做降低了false pos和neg的概率，使S曲线更接近于理想状态。当然同时也增加了hash计算的时间。

S曲线：

 

[LSH s曲线分析：海量数据挖掘MMDS week2: 局部敏感哈希Locality-Sensitive Hashing, LSH]

Compose construction

{and/or构造的组合使用}

And or compositon

这里and构造中的hash函数要有r个，or构造中的hash函数要有b个，这样才能将之前的两个概率表达转换成1-(1-p^r)^b的S曲线形式。

实例

Or and composition

实例

级联casecading construction

上面的级联等价于先应用4路or，再用16路and，最后4路or。That would be the same as applying a four-way OR then a 16-way,AND and Finally another four-way OR.

使用minhash函数的数目：每个构造需要16个原始hash函数才能构造成4，4的or-and（反推得到，1个F''中的hash函数需要4个F'中的hash函数来构造，而1个F‘中的hash函数又需要4个F中的hash函数构造），通过级联两个构造就使用了256个minhash函数。Notice that each construction uses 16 of the original functions.So by cascading these two constructions,we use 256 minhash functions.

实例

S-Curves

{阈值的选择}

阈值选择为函数f(S) = (1-S^r)^b的不动点（近似值），也就是输入一个相似度S，得到一个相同的概率p（hash到同一个bucket中的概率）。当相似性相对不动点变大时，其hash到同一个bucket中的概率也变大，反之相似性相对不动点变小时，其hash到同一个bucket中的概率也变小了。

总结

这样做之后，原有的hash函数族(d1,d2,p1,p2)-敏感的函数族如(0.3,0.7,0.7,0.3)，也就是当两个signatures的距离小于0.3时其hash后相似的概率为0.7，距离大于0.7的两个signatures其hash后相似的概率为0.3。

但是我们通过and-or函数级联后，hash函数族就变为如(0.3,0.7,0.9,0.1)，也就是当两个signatures的距离小于0.3时其hash后相似的概率为0.9，距离大于0.7的两个signatures其hash后相似的概率为0.1。这样模型的false postive和false negtive都降低了，模型变好了！

皮皮blog

面向其它距离度量的LSH函数族

{不是所有距离度量都存在LSH函数族}

Distance Measures距离度量方法

{除了jaccard similarity外， or distance and Beside it is possible to combine hash functions from a family,to get the s curve affect that we saw for LSH applied to min-hash matrices.In fact, the construction is essentially the same for any LSH family.And we'll conclude this unit by seeing some particular LSH families, and how they work for the cosine distance and Euclidean distance.}

距离度量公理，欧氏跨度

...

非欧氏距离

[ 距离和相似度度量方法]

面向海明距离的LSH函数族

海明距离的LSH函数族的规模最多为d，因为只要所有i(i=1~d)，hash函数fi(x)=fi(y)，则f(x)=f(y)。i大于向量长度d是没有效果的。

[距离和相似性度量方法-汉明距离-分类数据点间的距离]

面向cosin距离的LSH函数族(random hyperplanes)

两个向量的余弦距离是它们的夹角。夹角越小，其相似度越高，成为候选pairs的概率应该越大。那么这个与夹角相关的概率怎么表示呢？

答案就是通过一个hash函数对这两个向量进行hash，而这个hash函数实际上只是一个随机的向量，通过这个随机向量与这两个要比较相似性的向量的内积来判定，如果好多个这样随机的向量与它们的内积是同号的（同正或同负，总是同号说明划分平面总是在x，y夹角外侧不在夹角内部），则说明这两个向量的夹角很小，相似性大，否则相似性小。原因及解释见下面的解析。

cosin距离LSH函数族如下表示

哈希函数的表示

通过某个随机平面的法向量（一个随机的向量）和要比较相似度的两个向量x,y的内积的正负来判定x,y是否相似，而同为正或者负（就是有相似性）的概率可以表示为1-theta/180。

这也就是说，面向cosin距离的LSH哈希函数就是一个向量v，并且其hash的buckets只有两个——正和负。

注意，当x，y在法向量对应的平面同一侧时，与法向量的内积才会同号。

概率分析

随机向量(法向量)的选择

选择的随机向量（也就是hash函数）中的分量可以只是1、-1，这样计算内积更快。

conin距离的LSH函数族实例

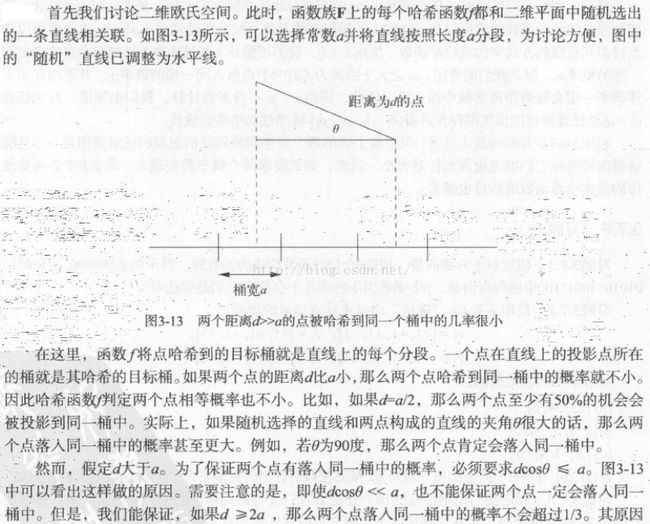
面向Euclidean距离的LSH函数族

对于欧氏距离，我们也想找到一个hash函数，当两点的距离相对较小时，hash函数hash两点到同一个桶中的概率很大。

概率分析

根据上述分析，两点距离大于2a时候，最多有1/3概率分到同一bucket中；然而距离小于a/2时，最少有1/2概率分到同一bucket中。而1/3和1/2的概率差不多是至少到满足的了，这样也就是说两点小距离和大距离至少要有4倍（2a/(a/2)）的差距才能很好的分离。

多维欧氏距离分析

根据上面的分析，大距离和小距离分开至少要4倍，也就是需要e > 4d。然而我们可以通过前面讲过的放大技术将后面的概率值调整到任意值附近。

皮皮blog

from:http://blog.csdn.net/pipisorry/article/details/48882167

ref: