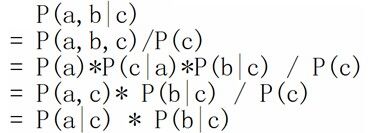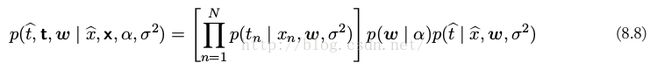PGM：有向图模型：贝叶斯网络

http://blog.csdn.net/pipisorry/article/details/52489270

为什么用贝叶斯网络

联合分布的显式表示

Note: n个变量的联合分布，每个x对应两个值，共n个x，且所有概率总和为1，则联合分布需要2^n-1个参数。

贝叶斯网表示

独立性质的应用会降低参数数目，表达更紧凑。

[PGM：贝叶斯网表示之朴素贝叶斯模型naive Bayes :独立性质的利用]

皮皮blog

贝叶斯网络

    贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。 

    贝叶斯网络的有向无环图中的节点表示随机变量，它们可以是可观察到的变量，或隐变量、未知参数等。认为有因果关系（或非条件独立）的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。总而言之，连接两个节点的箭头代表此两个随机变量是具有因果关系，或非条件独立。

    例如，假设节点E直接影响到节点H，即E→H，则用从E指向H的箭头建立结点E到结点H的有向弧(E,H)，权值(即连接强度)用条件概率P(H|E)来表示，如下图所示：

    简言之，把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖，用圈表示随机变量(random variables)，用箭头表示条件依赖(conditional dependencies)。

贝叶斯网的边的指向代表节点对其指向节点的直接影响？

模型：联合概率的表示

    令G = (I,E)表示一个有向无环图(DAG)，其中I代表图形中所有的节点的集合，而E代表有向连接线段的集合，且令X = (Xi)i ∈ I为其有向无环图中的某一节点i所代表的随机变量，若节点X的联合概率可以表示成：

则称X为相对于一有向无环图G 的贝叶斯网络，其中， 表示节点i之“因”，或称pa(i)是i的parents（父母）。 

此外，对于任意的随机变量，其联合概率可由各自的局部条件概率分布相乘而得出：

    

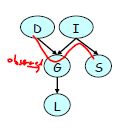
更复杂的学生示例

Note: 这里给出的概率都是条件概率而不是联合概率，如i0, d0  g1值0.3表示p(g1 | i0, d0)。
且从图中可知，这里I和D是独立的。

局部概率模型

模型表示

 推理模式

考虑贝叶斯网Bstudent，并观察当证据获得时各种事件的概率如何变化。
当我们只有部分证据时，要想推理某个概率，要对结果进行重新归一化。

因果推理和预测

p(l1)概率值的推导过程：


p(l1 | i0)的推导过程：

证据推理和解释

解释消除

相同结果的不同原因可以互相影响。

贝叶斯网的基本独立性：局部独立性

节点只直接依赖其父节点是贝叶斯网语义的核心。



但是G和L还是有关系的

给定节点父节点时，搜索独立性时实际上搜索的是边缘独立性。


直觉告诉我们，变量的父节点将其从具有因果关系的性质的概率影响中屏蔽了。也就是说，一旦知道了一个 节点的父节点的值，那么与其父节点或其它祖先节点直接或间接相关的任何信息都不会影响到该节点的可信度。不过，与其后代节点相关的信息仍然可以通过证据推理过程来改变我们关于它的判断。

贝叶斯网语义

图与分布

{CPD参数化有向图，给图结构关联一个参数集}
贝叶斯网图的形式化语义是一系列独立性断言。另一方面，学生贝叶斯网是由条件概率分布作注释的图，这个图通过链式法则为贝叶斯网定义了一个联合分布。这里将证明这两个定义实际上是等价的。分布P满足与图G相关的局部独立性，当且仅当P可以由与图G相关的一系列条件概率分布表示。

I-MAP

与P相关的独立性集合。

Note: 这个定义，尤其是I(G)包含于I(P)这个表示，说明G上的独立性P都满足，但是反过来P上的独立性G不一定都满足。
Note: 关于贝叶斯网，I-map的概念本身是不充分的：完备图意味着不存在独立性假设，因此是任意分布的一个I-map。

I-MAP到因子分解

由贝叶斯网的条件独立性假设，有下式成立

结果告诉我们， 联合分布中的任何表值都可以通过每个变量所对应的因子的乘积来计算。每个因子表示一个变量在网络中给定父节点时的条件概率。在G是I-MAP条件下，这种因子分解可以应用于任何分布P。
贝叶斯网链式法则和局部概率模型

Note: 条件概率链式法则

独立参数个数

学生示例中15个独立参数，联合分布的完全赋值需要47个独立参数。
更一般的

因子分解到I-MAP

知识工程

变量选择

概率选择





皮皮blog

图中的独立性：全局独立性

贝叶斯网中的独立性的两种定义：局部独立性（给定父节点条件下，每个节点都独立于它的非后代节点）和由d-分离导出的全局独立性。这两种独立性集合间相互蕴含，实际上是等价的。

d-分离

了解何时可以保证独立性条件 在与贝叶斯网结构G相关的分布中成立。尝试理解在变量Z的证据存在的条件下，何时考虑变量X的一个观察值有可能改变我们对Y的判断。
 

1 直接连接

2 间接连接

间接的因果作用图a(间接的证据作用图b)
如果可以观察到Z，那么X不会通过Z作用于Y(那么Y不会通过Z作用于X)。
共同的原因图c


X可以通过Z来影响Y，仅限于没有观察到Z的以情形。
共同的作用d

如果没有观察到中间节点Z，那么影响无法沿着迹X->Z<-Y流动。



如果观察到中间节点Z或者其子节点，那么影响就沿着迹X->Z<-Y流动。

有效迹

全局马尔可夫独立性：d-分离

可靠性与完备性

可靠性soundness：如果给定某个Z时，找到两个节点X与Y是d-分离的，那么可以保证，在给定Z时它们实际上是条件独立的。
互补性质 完备性completness: d-分离可以检测出所有可能的独立性。如果两个变量X和Y，且它们在给定Z时相互独立，那么它们是d-分离的。
。。。

d-分离算法
。。。
I-等价性
。。。

从分布到图

最小i-map

找到分布P的图的一种方法是简单地给出P的任何一个I-map图。

。。。

p-map

在给定的分布P中找到可以准确刻画所有独立性的图G。

。。。
发现p-map
。。。
皮皮blog

贝叶斯网络图模型的表示2

    为了理解有向图对于描述概率分布的作用,首先考虑三个变量 a, b, c 上的一个任意的联合分布 p(a, b, c) 。注意,现阶段我们不需要对这些变量做出任何更多的假设,例如它们是离散的还是连续的。实际上,图模型的一个强大的方面是,一个具体的图可以描述一大类概率分布。通过使用概率的乘积规则(1.11),我们可以将联合概率分布写成下面的形式。
p(a, b, c) = p(c | a, b)p(a, b)            (8.1)
再次使用乘积规则,这次处理方程(8.1)右侧的第二项,我们有
p(a, b, c) = p(c | a, b)p(b | a)p(a)           (8.2)
注意,这个分解方法对于任意的联合概率分布的选择都成立。

简单的图模型表示

    现在,我们使用一个简单的图模型表示方程(8.2)的右侧,如下所述。首先,我们为每个随机变量 a, b, c 引入一个结点,然后为每个结点关联上公式(8.2)右侧的对应的条件概率。然后,对于每个条件概率分布,我们在图中添加一个链接(箭头),链接的起点是条件概率的条件中的随机变量对应的结点。因此,对于因子 p(c | a, b) ,会存在从结点 a, b 到结点 c 的链接,而对于因子 p(a) ,没有输入的链接。结果就是图8.1中的图。如果存在一个从结点 a 到结点 b 的链接,那么我们说结点 a 是结点 b 的父结点,结点 b 是结点 a 的子结点。注意,我们不会形式化地区分结点和结点对应的变量,而是简单地使用同样的符号表示两者。关于公式(8.2),很有趣的一点是,它的左侧关于三个变量 a, b, c 是对称的,而右侧不是。实际上,通过进行公式(8.2)的分解,我们隐式地选择了一个特定的顺序(即 a, b, c )。如果选择一个不同的顺序,我们会得到一个不同的分解方式,因此就得到一个不同的图表示形式。

K变量联合概率分布的图模型表示

    我们将图8.1给出的例子扩展到 K 个变量的联合概率分布 p(x 1 , . . . , x K ) 。通过重复使用概率的乘积规则,联合概率分布可以写成条件概率的乘积,每一项对应一个变量,形式如下
p(x 1 , . . . , x K ) = p(x K | x 1 , . . . , x K−1 ) . . . p(x 2 | x 1 )p(x 1 )    (8.3)
对应一个给定的 K ,我们可以将其表示为一个具有 K 个结点的有向图,每个结点对应于公式(8.3)右侧的一个条件概率分布,每个结点的输入链接包括所有以编号低于当前结点编号的结点为起点的链接。我们说,这个图是全连接的( fully connected ),因为每对结点之间都存在一个链接。

缺失连接图表示

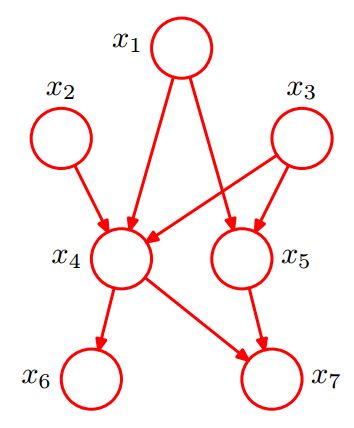
    目前为止,我们操作的对象是一个完全一般的联合概率分布,从而分解方式以及对应的全连接图表示,可以应用于概率分布的任意选择。正如我们将会看到的,真正传递出图表示的概率分布的性质的有趣信息的是图中链接的缺失( absence )。考虑图8.2的图。这不是一个全连接的图,因为从 x 1 到 x 2 或者从 x 3 到 x 7 之间不存在链接。
现在,我们将根据这幅图,写出对应的联合概率表达式。联合概率表达式由一系列条件概率的乘积组成,每一项对应于图中的一个结点。每个这样的条件概率分布只以图中对应结点的父结点为条件。例如, x 5 以 x 1 和 x 3 为条件。于是,7个变量的联合概率分布为

p(x 1 )p(x 2 )p(x 3 )p(x 4 | x 1 , x 2 , x 3 )p(x 5 | x 1 , x 3 )p(x 6 | x 4 )p(x 7 | x 4 , x 5 )        (8.4)

有向图和变量的概率分布间的一般关系

    我们现在说明给定的有向图和变量上对应的概率分布之间的一般关系。在图的所有结点上定义的联合概率分布由每个结点上的条件概率分布的乘积表示,每个条件概率分布的条件都是图中结点的父结点所对应的变量。因此,对于一个有 K 个结点的图,联合概率为

其中, pa k 表示 x k 的父结点的集合, x = {x 1 , . . . , x K } 。这个关键的方程表示有向图模型的联合概率分布的分解( factorization )属性。虽然我们之前考虑的情况是每个结点对应于一个变量的情形,但是我们可以很容易地推广到让图的每个结点关联一个变量的集合,或者关联向量值的变量。很容易证明,如果公式(8.5)右侧的每一个条件概率分布都是归一化的,那么这个表示方法整体总是归一化的。

贝叶斯网络的3种结构形式

对于下面的贝叶斯网络：

1. x1,x2,…x7的联合分布为

2. x1和x2独立（对应head-to-head）；

3. x6和x7在x4给定的条件下独立（对应tail-to-tail）。

D-Separation（D-分离）

    D-Separation是一种用来判断变量是否条件独立的图形化方法。换言之，对于一个DAG(有向无环图)E，D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。

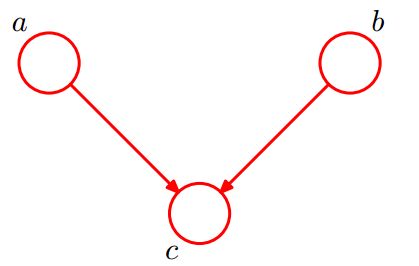
形式1 head-to-head

有P(a,b,c) = P(a)*P(b)*P(c|a,b)，积分c后可得：

即在c未知的条件下，a、b被阻断(blocked)，是独立的，称之为head-to-head（ 因 为 它 连 接 了 两 个 箭 头 的 头）条件独立。

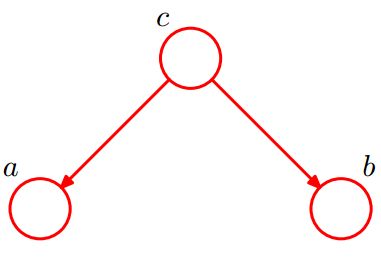
形式2 tail-to-tail

      

考虑c未知，跟c已知这两种情况：

    在c未知的时候，有：P(a,b,c)=P(c)*P(a|c)*P(b|c)，此时，没法得出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。

    在c已知的时候，有：P(a,b|c)=P(a,b,c)/P(c)，然后将P(a,b,c)=P(c)*P(a|c)*P(b|c)带入式子中，得到：P(a,b|c)=P(a,b,c)/P(c) = P(c)*P(a|c)*P(b|c) / P(c) = P(a|c)*P(b|c)，即c已知时，a、b独立。

所以，在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为tail-to-tail条件独立。

Any node is d-seperated from its non-descendants given its parents.父节点已知后，其它节点就不能通过父节点影响该节点的值了。

形式3 head-to-tail

     

还是分c未知跟c已知这两种情况：

    c未知时，有：P(a,b,c)=P(a)*P(c|a)*P(b|c)，但无法推出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。

    c已知时，有：P(a,b|c)=P(a,b,c)/P(c)，且根据P(a,c) = P(a)*P(c|a) = P(c)*P(a|c)，可化简得到：

所以，在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为head-to-tail条件独立。

head-to-tail其实就是一个链式网络：

马尔科夫链（Markov chain）

    根据head-to-tail，在xi给定的条件下，xi+1的分布和x1,x2…xi-1条件独立。意味着xi+1的分布状态只和xi有关，和其他变量条件独立。也就是当前状态只跟上一状态有关，跟之前的状态无关。这种顺次演变的随机过程，就叫做马尔科夫链（Markov chain）。也就是：

D-Separation的3种情况的总结

{即贝叶斯网络的3种结构形式}

 

head-to-tail，给定 T 时，A 和 X 独立；tail-to-tail，给定S时，L和B独立；head-to-head，未给定D时，L和B独立。

有向图d-划分性质的一般叙述

    考虑一个一般的有向图,其中 A, B, C 是任意无交集的结点集合(它们的并集可能比图中结点的完整集合要小)。我们希望弄清楚,一个有向无环图是否暗示了一个特定的条件依赖表述。我们考虑从 A 中任意结点到 B 中任意结点的所有可能的路径。
我们说这样的路径被“阻隔”,如果它包含一个结点满足下面两个性质中的任何一个:
    • 路径上的箭头以头到尾或者尾到尾的方式交汇于这个结点,且这个结点在集合 C 中，也就是A和B的“head-to-tail型”和“tail-to-tail型”路径都通过C。
    • 箭头以头到头的方式交汇于这个结点,且这个结点和它的所有后继都不在集合 C 中，也就是A和B的“head-to-head型”路径不通过C以及C的子孙。
如果所有的路径都被“阻隔”（上面两个条件均满足）,那么我们说 C 把 A 从 B 中 d -划分开,且图中所有变量上的联合概率分布将会满足 。

Note: 这里C是已知的，A和B的“head-to-tail型”和“tail-to-tail型”路径都通过C则AB条件独立；A和B的“head-to-head型”路径不通过C以及C的子孙，否则根据1在C已知的情况下AB就不独立了。

皮皮blog

示例：贝叶斯多项式回归

1.2.6曲线拟合问题

    在曲线拟合问题中,我们知道训练数据 x 和 t ,以及一个新的测试点 x ,我们的目标是预测 t 的值。因此我们想估计预测分布 p(t | x, x, t) 。这里我们要假设参数 α 和 β 是固定的,事先知道的(后续章节中我们会讨论这种参数如何通过贝叶斯方法从数据中推断出来)。简单地说,贝叶斯方法就是自始至终地使用概率的加和规则和乘积规则。因此预测概率可以写成下面的形式

p(t | x, x, t)  = ∫p(t | x, w)p(w | x, t) d w

随机变量联合概率分布的表示

    作为有向图描述概率分布的一个例子,我们考虑1.2.6节介绍的贝叶斯多项式拟合模型。这个模型中的随机变量是多项式系数向量 w 和观测数据 t = (t 1 , . . . , t N ) T 。此外,这个模型包含输入数据 x = (x 1 , . . . , x N ) T 、噪声方差 σ 2 以及表示 w 的高斯先验分布的精度的超参数 α 。所有这些都是模型的参数而不是随机变量。
现阶段我们只关注随机变量,我们看到联合概率分布等于先验概率分布 p(w) 与 N 个条件概率分布 p(t n | w) 的乘积( n = 1, . . . , N ),即
（lz：8.6和p(w | x, t)是正比的）
图模型表示的联合概率分布如图8.3所示。

复杂模型的板( plate )表示

    当我们开始处理更加复杂的模型时,我们会看到,像图8.3那样显式地写出 t 1 , . . . , t N 的结点是很不方便的。于是,我们引入一种图结构,使得多个结点可以更简洁地表示出来。这种图结构中,我们画出一个单一表示的结点 t n ,然后用一个被称为板( plate )的方框圈起来,标记为 N ,表示有 N 个同类型的点。用这种方式重新表示图8.3,我们得到了图8.4所示的图。

显式表示参数和随机变量

    我们有时会发现,显式地写出模型的参数和随机变量是很有帮助的。此时,公式(8.6)就变成了

对应地,我们可以在图表示中显式地写出 x 和 α 。为了这样做,我们会遵循下面的惯例:随机变量由空心圆表示,确定性参数由小的实心圆表示。如果我们让图8.4包含确定性参数,我们就得到了图8.5。

观测变量和潜在变量

    当我们将图模型应用于机器学习或者模式识别的问题中时,我们通常将某些随机变量设置为具体的值,例如将变量 {t n } 根据多项式曲线拟合中的训练集进行设置。在图模型中,我们通过给对应的结点加上阴影的方式来表示这种观测变量( observed variables )。于是,图8.5所示的图中,如果 {t n } 是观测变量,那么就变成了图8.6。注意, w 不是观测变量,因此 w 是潜在变量( latent variable )的一个例子。潜在变量也被称为隐含变量( hidden variable )。

系数 w 的的后验概率

观测到了 {t n } 的值,如果必要的话,我们可以计算系数 w 的的后验概率。现阶段,我们注意到,这是贝叶斯定理的一个直接应用。

观测数据为条件的t 的概率分布

其中,我们再一次省略了确定性参数,使得记号简洁。

通常,我们对于 w 这样的参数本身不感兴趣,因为我们的最终目标是对输入变量进行预测。假设给定一个输入值 x ,我们想找到以观测数据为条件的对应的 t 的概率分布。描述这个问题的图模型如图8.7所示。以确定性参数（x）为条件,这个模型的所有随机变量（t, w）的联合分布为

然后,根据概率的加和规则,对模型参数 w 积分,即可得到 t 的预测分布

其中我们隐式地将 t 中的随机变量设置为数据集中观测到的具体值。

皮皮blog

生成式模型

祖先取样( ancestral sampling )

    许多情况下,我们希望从给定的概率分布中抽取样本。这里简要介绍祖先取样( ancestral sampling ),与图模型特别相关。考虑 K 个变量的一个联合概率分布 p(x 1 , . . . , x K ) ,它根据公式(8.5)进行分解,对应于一个有向无环图。我们假设变量已经进行了排序,从而不存在从某个结点到序号较低的结点的链接。换句话说,每个结点的序号都大于它的父结点。我们的目标是从这样的联合概率分布中取样 x 1 , . . . , x K

为了完成这一点,我们首先选出序号最小的结点,按照概率分布 p(x 1 ) 取样,记作 x 1 。然后,我们顺序计算每个结点,使得对于结点 n ,我们根据条件概率 p(x n | pa n ) 进行取样,其中父结点的变量被设置为它们的取样值。注意,在每个阶段,这些父结点的变量总是可以得到的,因为它们对应于已经采样过的序号较小的结点。按照具体的概率分布的取样方法将会在第11章详细讨论。一旦我们对最后的变量 x K 取样结束,我们就达到了根据联合概率分布取样的目标。为了从对应于变量的子集的边缘概率分布中取样,我们简单地取要求结点的取样值,忽略剩余结点的取样值。例如,为了从概率分布 p(x 2 , x 4 ) 中取样,我们简单地对联合概率分布取样,然后保留 x 2 , x 4 ,丢弃剩余的值 {x j̸ =2,4 } 。

概率模型的实际应用

    对于概率模型的实际应用,通常的情况是,数量众多的变量对应于图的终端结点(表示观测值),较少的变量对应于潜在变量。潜在变量的主要作用是使得观测变量上的复杂分布可以表示为由简单条件分布(通常是指数族分布)构建的模型。

我们可以将这样的模型表示为观测数据产生的过程。例如,考虑一个模式识别的任务,其中每个观测值对应于一幅图像(由像素灰度值的向量组成)。这种情况下,潜在变量可以看成物体的位置或者方向。给定一个特定的观测图像,我们的目标是找到物体上的后验概率分布,其中我们对于所有可能的位置和方向进行了积分。我们可以使用图8.8的图模型表示这个问题。

The image (a vectorof pixel intensities) has a probability distribution thatis dependent on the identity of the object as well ason its position and orientation.

生成式模型( generative model )

    图模型描述了生成观测数据的一种因果关系( causal )过程( Pearl, 1988 )。因此,这种模型通常被称为生成式模型( generative model )。相反,图8.5描述的多项式回归模型不是生成式模型,因为没有与输入变量 x 相关联的概率分布,因此无法从这个模型中人工生成数据点。通过引入合适的先验概率分布 p(x) ,我们可以将模型变为生成式模型,代价是增加了模型的复杂度。

然而,概率模型中的隐含变量不必具有显式的物理含义。它的引入可以仅仅为了从更简单的成分中建立一个更复杂的联合概率分布。在任何一种情况下,应用于生成式模型的祖先取样方法都模拟了观测数据的创造过程,因此可以产生“幻想的”数据,它的概率分布(如果模型完美地表示现实)与观测数据的概率分布相同。在实际应用中,从一个生成式模型中产生人工生成的观测数据,对于理解模型所表示的概率分布形式很有帮助。

皮皮blog

离散变量

{如何在一组离散变量上构建联合概率分布}

    指数族概率分布将许多著名的概率分布当成了指数族分布的特例。虽然指数族分布相对比较简单,但是它们组成了构建更复杂概率分布的基本元件。图模型的框架在表达这些基本元件之间的联系时非常有用。

    如果我们将有向图中的每个父结点-子结点对的关系选为共轭的,那么这样的模型有一些特别好的性质,我们稍后会给出几个例子。两种情形很值得注意,即父结点和子结点都对应于离散变量的情形,以及它们都对应高斯变量的情形,因为在这两种情形中,关系可以层次化地推广,构建任意复杂的有向无环图。我们首先考察离散变量的情形。

一元离散变量概率分布表达式

    对于有着 K 个可能状态(使用“1- of - K ”表达方式)的一元离散变量 x ,概率 p(x | μ) 为

(lz：多项式分布)

并且由参数 μ = (μ 1 , . . . , μ K ) T 控制。由于限制条件 k μ k = 1 的存在,因此为了定义概率分布,只需要指定 K − 1 个 μ k 的值即可。

多元离散变量概率分布表达式

    现在假设我们有两个离散变量 x 1 和 x 2 ,每个都有 K 个状态,我们项对它们的联合概率分布建模。我们将 x 1k = 1 和 x 2l = 1 同时被观测到的概率记作参数 μ kl ,其中 x 1k 表示 x 1 的第 k 个分量, x 2l 的意义与此相似。联合概率分布可以写成

由于参数 μ kl 满足限制条件 ,因此这个分布由 K^ 2 − 1 个参数控制。很容易看到,对于 M 个变量的任意一个联合概率分布,需要确定的参数的数量为 K ^M − 1 ,因此随着变量 M 的数量指数增长。

减小模型中独立参数数量

1 减少图链接

    使用概率的乘积规则,我们可以将联合概率分布 p(x 1 , x 2 ) 分解为 p(x 2 | x 1 )p(x 1 ) ,它对应于一个具有两个结点的图,链接从结点 x 1 指向结点 x 2 ,如图8.9(a)所示。边缘概率分布 p(x 1 ) 与之前一样,由 K − 1 个参数控制。类似地,条件概率分布 p(x 2 | x 1 ) 需要指定 K − 1 个参数,确定 x 1 的 K 个可能的取值。因此,与之前一样,在联合概率分布中,需要指定的参数的总数为 (K − 1) + K(K − 1) = K ^ 2 − 1 。

现在假设变量 x 1 和 x 2 是独立的,对应于图8.9(b)所示的图模型。这样,每个变量由一个独立的多项式概率分布描述,参数的总数是 2(K − 1) 。对于 M 个独立离散变量上的概率分布,其中每个变量有 K 个可能的状态,参数的总数为 M (K − 1) ,因此随着变量的数量线性增长。从图的角度看,我们通过删除结点之间链接的方式,减小了参数的数量,代价是类别的概率分布受到了限制。

更一般地,如果我们有 M 个离散变量 x 1 , . . . , x M ,那么我们可以使用有向图来对联合概率分布建模,每个变量对应于一个结点。每个结点的条件概率分布由一组非负参数给出,同时需要满足归一化限制条件。如果图是全连接的,那么我们有一个完全一般的概率分布,这个分布有 K M − 1 个参数。而如果图中不存在链接,那么联合概率分布可以分解为边缘概率分布的乘积,参数的总数为 M (K − 1) 。连接度处于二者之间的图使得模型能够处理比完全分解的概率分布更加一般的概率分布,同时参数的数量比一般的联合概率分布的参数数量少。作为一个说明,考虑图8.10所示的结点链。边缘概率分布 p(x 1 ) 需要 K − 1 个参数,而对于 M − 1 个条件概率分布 p(x i | x i−1 ) (其中 i = 2, . . . , M )需要 K(K − 1) 个参数。从而,参数的总数为 K − 1 + (M − 1)K(K − 1) ,这是 K 的二次函数,并且随着链的长度 M 线性增长(而不是指数增长)。

2 参数共享

    另一种减小模型中独立参数数量的方法是参数共享(sharing),也被称为参数捆扎(tying)。例如,在图8.10给出的结点链的例子,我们可以使所有的条件概率分布p(xi|xi−1)(其中i=2,...,M)由同样的参数集合K(K−1)。加上控制x1的K−1个参数,为了定义联合概率分布所需指定的参数的总数为K2−1。   

    贝叶斯模型：引入参数的狄利克雷先验

    通过引入参数的狄利克雷先验,我们可以将离散变量上的图模型转化为贝叶斯模型。从图的观点来看,每个结点需要额外的父结点表示对应于每个离散结点的参数。这种情况在图8.11中进行了说明。

如果我们将控制条件概率分布 p(x i | x i−1 ) (其中 i = 2, . . . , M )的参数进行参数共享,那么对应的模型如图8.12所示。

3 对条件概率分布使用参数化的模型

    另一种控制离散变量模型参数数量的指数增长的方式是对条件概率分布使用参数化的模型,而不使用条件概率值的完整表格。为了说明这个想法,考虑图8.13所示的图,其中所有的结点表示二值变量。每个父结点变量 x i 由单一参数 μ i 控制,这个参数表示概率 p(x i = 1) ,从而对于 M 个父结点,参数总数为 M 。但是,条件概率分布 p(x 1 , . . . , x M ) 需要 2 M 个参数,每个参数表示 2 M 种父结点变量的可能配置下的概率 p(y = 1) 。因此,通常来说,确定这个条件概率分布的参数的数量会随着 M 指数增长。将 logistic sigmoid 函数作用于父结点变量的线性组合上,我们可以得到一个更加简洁的条件概率分布,形式为

其中σ(a)=(1+exp(−a))^−1是一个logisticsigmoid函数,x=(x0,x1,...,xM)T是一个(M+1)维向量,表示父结点的M个状态加上一个额外的变量x0,其值被固定为1。w=(w0,w1,...,wM)T是一个M+1个参数的向量。与一般的情形相比,这是一个更加受限形式的条件概率分布,但是参数的数量随着M线性增长。在这种情况下,类似于选择多元高斯分布的协方差矩阵的限制形式(例如对角矩阵)。

皮皮blog

线性高斯模型

{多元高斯分布如何表示为一个对应于成分变量上的线性高斯模型的有向无环图}

    说明多元高斯分布如何表示为一个对应于成分变量上的线性高斯模型的有向无环图。这使得我们在概率分布上施加有趣的结构,这些结构中的两个相反的极端情况是一般的高斯分布和对角化协方差高斯分布。几种广泛使用的方法是线性高斯模型的例子,例如概率主成分分析,因子分析,以及线性动态系统( Roweis and Ghahramani,1999 )。

多元高斯分布的联合概率分布 p(x)

    考虑 D 个变量上的任意的有向无环图,其中结点 i 表示服从高斯分布的一元连续随机变量 x i 。这个分布的均值是结点 i 的父结点pa i 的状态的线性组合,即

其中 w ij 和 b i 是控制均值的参数, v i 是 x i 的条件概率分布的方差。这样,联合概率分布的对数为图中所有结点上的这些条件分布的乘积的对数,因此形式为

其中 x = (x 1 , . . . , x D ) T ,“常数”表示与 x 无关的项。我们看到这是 x 的元素的二次函数,因此联合概率分布 p(x) 是一个多元高斯分布。

递归计算联合概率分布的均值和方差

    我们可以递归地确定联合概率分布的均值和方差,方法如下。每个变量 x i 的概率分布都是(以父结点状态为条件的)高斯分布,形式为公式(8.11)所示。因此

其中 ε i 是一个零均值单位方差的高斯随机变量,满足 E[ε i ] = 0 且 E[ε i ε j ] = I ij ,其中 I ij 是单位矩阵的第 i, j 个元素。对公式(8.14)取期望,我们有

这 样, 从 一 个 序 号 最 低 的 结 点 开 始, 沿 着 图 递 归 地 计 算, 我 们 就 可 以 求出 E[x] = (E[x 1 ], . . . , E[x D ]) T 的各个元素。这里,我们再一次假设所有结点的序号都大于它的父结点的句号。类似地,我们可以使用公式(8.14)和(8.15),以递归的方式得到 p(x) 的协方差矩阵的第 i, j 个元素,即

因此协方差可以从序号最低的结点开始,递归地计算。

两 个 极 端 的 情 形

让 我 们 考 虑 两 个 极 端 的 情 形。
    首 先, 假 设 图 中 不 存 在 链 接, 因 此 图 由 D 个 孤 立 的 结 点组 成。 在 这 种 情 况 下, 不 存 在 参 数 w ij , 因 此 只 有 D 个 参 数 b i 和 D 个 参 数 v i 。 根 据 递 归 关 系(8.15)和(8.16),我们看到 p(x) 的均值为 (b 1 , . . . , b D ) T ,协方差矩阵是一个对角矩阵,形式为diag (v 1 , . . . , v D ) 。联合概率分布总计有 2D 个参数,表示 D 个独立的一元高斯分布组成的集合。

    现在考虑一个全连接的图,其中每个结点的序号都低于其父结点的序号。这样矩阵 w ij 的第 i 行有 i − 1 项,因此矩阵是一个下三角矩阵(主对角线上没有元素)。参数 w ij 的数量从而可以通过下面的方式得到:取 D × D 的元素个数 D^2 ,减去 D ,表示主对角线上没有元素,再除以2,因为矩阵只在对角线下方存在元素,从而参数的总数为 D(D−1)/2。独立参数 {w ij } 加上协方差矩阵中的 {v i } ,因此独立参数的总数为 D(D+1)/2 ,对应于一个一般的对称协方差矩阵。

复杂度处于两种极端情况之间

    复杂度处于两种极端情况之间的图对应于协方差矩阵取特定形式的联合高斯分布。考虑图8.14中的图,它在变量 x 1 和 x 3 之间不存在链接。使用递归关系(8.15)和(8.16),我们看到联合高斯分布的均值和协方差为

我们已经可以将线性高斯图模型扩展到结点表示多元高斯变量的情形。在这种情况下,我们可以将结点 i 的条件概率分布写成下面的形式

现在 W ij 是一个矩阵。如果 x i 和 x j 的维度不同,那么 W ij 不是方阵。与之前一样,很容易证明所有变量上的联合概率分布是高斯分布。

注意,我们已经看到高斯变量 x 的均值 μ 的共轭先验本身是 μ 上的一个高斯分布。此时我们已经遇到了线性高斯关系的一个具体的例子。因此 x 和 μ 的联合分布就是高斯分布。这对应于一个简单的具有两个结点的图,其中表示 μ 和结点是表示 x 的结点的父结点。 μ 上的概率分布的均值是控制先验分布的参数,因此它可以被看做超参数。由于超参数的值本身是未知的,因此我们可以再一次使用贝叶斯的观点,引入一个超参数上的先验概率分布。这个先验概率分布有时被称为超先验( hyperprior ),它还是一个高斯分布。这种构造过程原则上可以延伸到任意层次。这个模型是层次贝叶斯模型( hierarchical Bayesian model )的一个例子。

贝叶斯网络的应用

from: http://blog.csdn.net/pipisorry/article/details/52489270

ref: prml chapter 8:GRAPHICAL MODELS

[概率图模型  原理与技术[（美）科勒，（以）弗里德曼著]*

贝叶斯网络 - 维基百科

贝叶斯网络简介

贝叶斯网络简介

算法杂货铺——分类算法之贝叶斯网络(Bayesian networks)