编码和加密算法的使用(MD5、Base64、DES、RSA)
- MD5:
- 不可逆,一般用于信息比对
- MD5值长度固定为128bit
- 容易计算
- 抗修改性
- 抗强碰撞,非常难伪造
//MD5在线解密,因为MD5具有不可逆的特点,所有对MD5解密也只是属于一中暴力解密(穷举法),但是依然可以破解一些比较常用的词或者句子
http://www.cmd5.com/
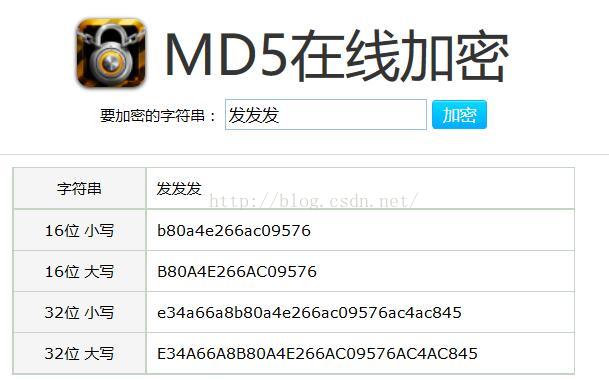
//MD5在线加密,可以将同一个字符串加密成不同位数的字符串
http://md5jiami.51240.com/
关于MD5加密作如下的简单介绍:
MD5的典型应用是对一段信息(Message)产生信息摘要(Message-Digest),以防止被篡改。比如,在UNIX下有很多软件在下载的时候都有一个文件名相同,文件扩展名为.md5的文件,在这个文件中通常只有一行文本,大致结构如:
MD5 (tanajiya.tar.gz) = 0ca175b9c0f726a831d895e269332461
这就是tanajiya.tar.gz文件的数字签名。MD5将整个文件当作一个大文本信息,通过其不可逆的字符串变换算法,产生了这个唯一的MD5信息摘要。为了让读者朋友对MD5的应用有个直观的认识,笔者以一个比方和一个实例来简要描述一下其工作过程:
大家都知道,地球上任何人都有自己独一无二的指纹,这常常成为公安机关鉴别罪犯身份最值得信赖的方法;与之类似,MD5就可以为任何文件(不管其大小、格式、数量)产生一个同样独一无二的“数字指纹”,如果任何人对文件名做了任何改动,其MD5值也就是对应的“数字指纹”都会发生变化。
我们常常在某些软件下载站点的某软件信息中看到其MD5值,它的作用就在于我们可以在下载该软件后,对下载回来的文件用专门的软件(如Windows MD5 Check等)做一次MD5校验,以确保我们获得的文件与该站点提供的文件为同一文件。利用MD5算法来进行文件校验的方案被大量应用到软件下载站、论坛数据库、系统文件安全等方面。
MD5的典型应用是对一段Message(字节串)产生fingerprint(指纹),以防止被“篡改”。举个例子,你将一段话写在一个叫 readme.txt文件中,并对这个readme.txt产生一个MD5的值并记录在案,然后你可以传播这个文件给别人,别人如果修改了文件中的任何内容,你对这个文件重新计算MD5时就会发现(两个MD5值不相同)。如果再有一个第三方的认证机构,用MD5还可以防止文件作者的“抵赖”,这就是所谓的数字签名应用。
MD5还广泛用于操作系统的登陆认证上,如Unix、各类BSD系统登录密码、数字签名等诸多方。如在UNIX系统中用户的密码是以MD5(或其它类似的算法)经Hash运算后存储在文件系统中。当用户登录的时候,系统把用户输入的密码进行MD5 Hash运算,然后再去和保存在文件系统中的MD5值进行比较,进而确定输入的密码是否正确。通过这样的步骤,系统在并不知道用户密码的明码的情况下就可以确定用户登录系统的合法性。这可以避免用户的密码被具有系统管理员权限的用户知道。MD5将任意长度的“字节串”映射为一个128bit的大整数,并且是通过该128bit反推原始字符串是困难的,换句话说就是,即使你看到源程序和算法描述,也无法将一个MD5的值变换回原始的字符串,从数学原理上说,是因为原始的字符串有无穷多个,这有点象不存在反函数的数学函数。所以,要遇到了md5密码的问题,比较好的办法是:你可以用这个系统中的md5()函数重新设一个密码,如admin,把生成的一串密码的Hash值覆盖原来的Hash值就行了。
正是因为这个原因,现在被黑客使用最多的一种破译密码的方法就是一种被称为"跑字典"的方法。有两种方法得到字典,一种是日常搜集的用做密码的字符串表,另一种是用排列组合方法生成的,先用MD5程序计算出这些字典项的MD5值,然后再用目标的MD5值在这个字典中检索。我们假设密码的最大长度为8位字节(8 Bytes),同时密码只能是字母和数字,共26+26+10=62个字符,排列组合出的字典的项数则是P(62,1)+P(62,2)….+P(62,8),那也已经是一个很天文的数字了,存储这个字典就需要TB级的磁盘阵列,而且这种方法还有一个前提,就是能获得目标账户的密码MD5值的情况下才可以。这种加密技术被广泛的应用于UNIX系统中,这也是为什么UNIX系统比一般操作系统更为坚固一个重要原因。
/**
*使用MD5编码
*/
public static String encrypt(String info){
String strDes = null;
try {
//获得使用MD5加密算法的编码对象
MessageDigest md = MessageDigest.getInstance("MD5");
//使用md5加密,生成byte数组,128位
byte[] data = md.digest(info.getBytes("utf-8"));
//将md5加密后的byte数组转成16进制的串
StringBuffer sb = new StringBuffer();
for (int i = 0; i < data.length; i++) {
//高位补0,只保留低位,避免出现负数,所以这里要与0xff做与运算
int n = data[i] & 0xff;
//转成16进制串
String hs = Integer.toHexString(n);
//如果是1位,就补0,最多2位,因为0xff能表示到255,8位byte数组最多表示255
if (hs.length() == 1){
hs = "0" + hs;
}
sb.append(hs);
}
strDes = sb.toString();
//strDes = sb.substring(8,24);//16位,从0开始计算,取第8(包括)个到第24个(不包括)字符
} catch (Exception e) {
e.printStackTrace();
}
return strDes;
}- BASE64
- 准确来讲,它是一种编码方式,有些协议传输非ASCII编码的时候需要使用base64编码后才能传输
- 可逆的,很容易解码
那么有人会问,既然很容易解密那么干嘛还要使用它来编码呢,目的出于什么?
Base64主要用于将不可打印的字符转换成可打印字符,或者简单的说将二进制数据编码成ASCII字符。
将二进制数据编码成ASCII字符主要的目的是能在纯文本内容中插入二进制数据,常见的应用场景包括:
-
电子邮件
这个可参考阮一峰的《MIME笔记》
-
微软的MHT格式
这是模仿邮件格式将多种资源打包在一个文件中的格式,所有二进制资源都采用 Base64 编码。
-
XML文件
这是一个纯文本文件,如果要基于 XML 格式设计可以保存图片或其它附件的数据格式,那就需要将这些二进制数据转码成 ASCII 字符。
-
DATA URL
最近流行起来的 Data URL,要在URL中使用二进制数据,当然也只能进行 ASCII 编码
当然除了 Base64 之外,还有其它一些编码方式可以将二进制数据编码成 ASCII 字符,比如十六进制编码,除此之外还有 Quoted-printable 等。甚至 URL 中使用 %XX 来对非 ASCII 字符进行编码的方式也可以算在内。
当然一般非特定环境下,选用十六进制编码和 Base64 编码的情况比较多,主要是因为这两种编码易用,而且转换后的数据量相对较小。
十六进制编码是将 1 个字节编码成 2 个十六进制字符,比如 0x10110110 编码成 B6,转换后数据量会增大 1 倍。
Base64 编码是将 3 个字节共 24 位数据,以每 6 位一个 Base64 字符 [0-9a-zA-Z+/] 表示,24 位数据共需要 4 个 Base64 字符表示,编码后数据增长约 1/3。为什么是“约”?因为如果原数据字节数不是 3 的倍数,需要补位,这样转换出来的数据量就会比原来的 4/3 略多一点。
post中的图片使用base64编码的情况
When you have some binary data that you want to ship across a network, you generally don't do it by just streaming the bits and bytes over the wire in a raw format. Why? because some media are made for streaming text. You never know -- some protocols may interpret your binary data as control characters (like a modem), or your binary data could be screwed up because the underlying protocol might think that you've entered a special character combination (like how FTP translates line endings).
话太多了直接上代码吧、看看下面的demo是不是觉得很简单呢
/**
* Base64编码和解码
* Created by LiuTao008
* on 2016/1/22.
*/
public class Base64Utils {
/**
* Base64编码
* @param strSrc 需要编码的字符串
* @return 编码后的字符串
*/
public static String encrypt(String strSrc){
String strBse64 ="";
byte[] bytes = Base64.encode(strSrc.getBytes(), Base64.DEFAULT);
strBse64 = new String(bytes);
return strBse64;
}
/**
* Base64解码
* @param strBase64 需要解码的base64串
* @return 解码后的串
*/
public static String decrypt(String strBase64){
String strDes = "";
byte[] bytes = Base64.decode(strBase64.getBytes(), Base64.DEFAULT);
strDes = new String(bytes);
return strDes;
}
}- 对称加密——DES
- 真正的加密算法,带密钥,加密和解密使用相同的密钥
- 对称加密优点是算法公开、计算量小、加密速度快、加密效率高
- 双方都保存秘钥,其次如果一方的秘钥被泄露,那么加密信息也就不安全了。另外,每对用户每次使用对称加密算法时,都需要使用其他人不知道的唯一秘钥,这会使得收、发双方所拥有的钥匙数量巨大,密钥管理成为双方的负担
- DES使用56位密钥,以现代计算能力,24小时内即可被破解。虽然如此,在某些简单应用中,我们还是可以使用DES加密算法
public class DES {
/**
* 加密
*
* @param datasource byte[]
* @param password String
* @return byte[]
*/
public static byte[] encrypt(byte[] datasource, String password) {
try {
SecureRandom random = new SecureRandom();
DESKeySpec desKey = new DESKeySpec(password.getBytes());
//创建一个密匙工厂,然后用它把DESKeySpec转换成
SecretKeyFactory keyFactory = SecretKeyFactory.getInstance("DES");
SecretKey securekey = keyFactory.generateSecret(desKey);
//Cipher对象实际完成加密操作
Cipher cipher = Cipher.getInstance("DES");
//用密匙初始化Cipher对象,Cipher.ENCRYPT_MODE代表编码模式
cipher.init(Cipher.ENCRYPT_MODE, securekey, random);
//现在,获取数据并加密
//正式执行加密操作
return cipher.doFinal(datasource);
} catch (Throwable e) {
e.printStackTrace();
}
return null;
}
/**
* 解密
*
* @param src byte[]
* @param password String
* @return byte[]
* @throws Exception
*/
public static byte[] decrypt(byte[] src, String password) throws Exception {
// DES算法要求有一个可信任的随机数源
SecureRandom random = new SecureRandom();
// 创建一个DESKeySpec对象
DESKeySpec desKey = new DESKeySpec(password.getBytes());
// 创建一个密匙工厂
SecretKeyFactory keyFactory = SecretKeyFactory.getInstance("DES");
// 将DESKeySpec对象转换成SecretKey对象
SecretKey securekey = keyFactory.generateSecret(desKey);
// Cipher对象实际完成解密操作
Cipher cipher = Cipher.getInstance("DES");
// 用密匙初始化Cipher对象
cipher.init(Cipher.DECRYPT_MODE, securekey, random);
// 真正开始解密操作
return cipher.doFinal(src);
}
}- 非对称加密--RSA
1、用RSA算法生成一对密钥,公钥发放给外部客户,私钥自己保管;有以下应用场景:
【公钥加密、私钥解密】或者【私钥签名、公钥验证】
2、非对称加解密的理解:
- 小明想秘密给小英发送消息
- 小英手里有一个盒子(public key),这个盒子只有小英手里的钥匙(private key)才打得开
- 小英把盒子送给小明(分发公钥)
- 小明写好消息放进盒子里,锁上盒子(公钥加密)
- 小明把盒子寄给小英(密文传输)
- 小英用手里的钥匙打开盒子,得到小明的消息(私钥解密)
- 假设小刚劫持了盒子,因为没有小英的钥匙,他也打不开
- 与DES不同,RSA算法中,每个通信主体都有两个钥匙,一个公钥一个私钥。
-
就是有2把钥匙
公私钥加解密举例
1。使用publicKey可以对数据进行加密
2。使用Key才能对数据进行解密
单方向传输
用公钥加密的数据,只有私钥能解开(可用于加密);
同时,使用私钥加密的数据,只有公钥能解开(签名)。但是速度很慢(比私钥加密慢100到1000倍),
公钥的主要算法有RSA,还包括Blowfish,Diffie-Helman等
公钥与私钥
1.权威数字认证机构(CA)给所有通信主体(个人或组织)颁发公钥和私钥,彼此配对,分别唯一。
2.私钥好比数字指纹,同时具有解密和加密功能。个人保管,不公开。
3.公钥好比安全性极高的挂号信箱地址,公开。 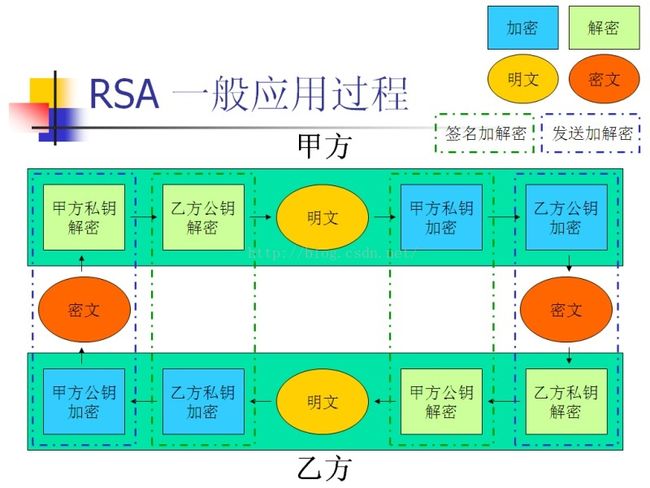
设若甲有一份需保密的数字商业合同发给乙签署。经过如下步骤:
1. 甲用乙的公钥对合同加密。
2. 密文从甲发送到乙。
3. 乙收到密文,并用自己的私钥对其解密。
4. 解密正确,经阅读,乙用自己的私钥对合同进行签署。
5. 乙用甲的公钥对已经签署的合同进行加密。
6. 乙将密文发给甲。
7. 甲用自己的私钥将已签署合同解密。
8. 解密正确,确认签署。
公私钥加解密说明
从以上步骤,我们知道:
1. 用公钥加密的密文能且只能用与其唯一配对的私钥才能解开。
2. 如果某份密文被解开,那么肯定是密文的目标信息主体解开的。
3. 私钥因其唯一标识所有者的属性,被用于数字签名,具有法律效力。
一。 公私钥生成
1.随机选定两个大素数p, q.
2.计算公钥和私钥的公共模数 n = pq .
3.计算模数n的欧拉函数 φ(n) .
4.选定一个正整数e, 使1 < e < φ(n) , 且e与φ(n)互质.
5.计算d, 满足 de ≡ 1 (mod φ(n) ), (k为某个正整数).
6.n与e决定公钥, n与d决定私钥.
二。加解密
该过程为小张给小李发消息,公钥为小李的公钥(n & e), 私钥为小李的私钥(n & d).
1.小张欲给小李发一个消息M, 他先把M转换为一个大数m < n, 然后用小李的公钥(n & e)把m加密为另一个大数:
c = me mod n
2.小李收到小张发来的大数c, 着手解密. 通过自己的私钥(n & d), 得到原来的大数m:
m = cd mod n
3.再把m转换为M, 小李即得到小张的原始消息.
这个过程之所以能通过, 是因为有如下等式:
cd ≡(me)d ≡med (mod n)
RSA详细算法如下:
1、RSA算法
它是第一个既能用于数据加密也能用于数字签名的算法。它易于理解和操作,也很流行。算法的名字以发明者的名字命名:Ron Rivest, Adi Shamir 和Leonard Adleman。但RSA的安全性一直未能得到理论上的证明。它经历了各种攻击,至今未被完全攻破。
一、RSA算法 :
首先, 找出三个数, p, q, r,
其中 p, q 是两个相异的质数, r 是与 (p-1)(q-1) 互质的数......
p, q, r 这三个数便是 private key
接著, 找出 m, 使得 rm == 1 mod (p-1)(q-1).....
这个 m 一定存在, 因为 r 与 (p-1)(q-1) 互质, 用辗转相除法就可以得到了.....
再来, 计算 n = pq.......
m, n 这两个数便是 public key
编码过程是, 若资料为 a, 将其看成是一个大整数, 假设 a < n....
如果 a >= n 的话, 就将 a 表成 s 进位 (s <= n, 通常取 s = 2^t),
则每一位数均小於 n, 然後分段编码......
接下来, 计算 b == a^m mod n, (0 <= b < n),
b 就是编码後的资料......
解码的过程是, 计算 c == b^r mod pq (0 <= c < pq),
於是乎, 解码完毕...... 等会会证明 c 和 a 其实是相等的 :)
如果第三者进行窃听时, 他会得到几个数: m, n(=pq), b......
他如果要解码的话, 必须想办法得到 r......
所以, 他必须先对 n 作质因数分解.........
要防止他分解, 最有效的方法是找两个非常的大质数 p, q,
使第三者作因数分解时发生困难.........
<定理>
若 p, q 是相异质数, rm == 1 mod (p-1)(q-1),
a 是任意一个正整数, b == a^m mod pq, c == b^r mod pq,
则 c == a mod pq
证明的过程, 会用到费马小定理, 叙述如下:
m 是任一质数, n 是任一整数, 则 n^m == n mod m
(换另一句话说, 如果 n 和 m 互质, 则 n^(m-1) == 1 mod m)
运用一些基本的群论的知识, 就可以很容易地证出费马小定理的........
<证明>
因为 rm == 1 mod (p-1)(q-1), 所以 rm = k(p-1)(q-1) + 1, 其中 k 是整数
因为在 modulo 中是 preserve 乘法的
(x == y mod z and u == v mod z => xu == yv mod z),
所以, c == b^r == (a^m)^r == a^(rm) == a^(k(p-1)(q-1)+1) mod pq
1. 如果 a 不是 p 的倍数, 也不是 q 的倍数时,
则 a^(p-1) == 1 mod p (费马小定理) => a^(k(p-1)(q-1)) == 1 mod p
a^(q-1) == 1 mod q (费马小定理) => a^(k(p-1)(q-1)) == 1 mod q
所以 p, q 均能整除 a^(k(p-1)(q-1)) - 1 => pq | a^(k(p-1)(q-1)) - 1
即 a^(k(p-1)(q-1)) == 1 mod pq
=> c == a^(k(p-1)(q-1)+1) == a mod pq
2. 如果 a 是 p 的倍数, 但不是 q 的倍数时,
则 a^(q-1) == 1 mod q (费马小定理)
=> a^(k(p-1)(q-1)) == 1 mod q
=> c == a^(k(p-1)(q-1)+1) == a mod q
=> q | c - a
因 p | a
=> c == a^(k(p-1)(q-1)+1) == 0 mod p
=> p | c - a
所以, pq | c - a => c == a mod pq
3. 如果 a 是 q 的倍数, 但不是 p 的倍数时, 证明同上
4. 如果 a 同时是 p 和 q 的倍数时,
则 pq | a
=> c == a^(k(p-1)(q-1)+1) == 0 mod pq
=> pq | c - a
=> c == a mod pq
Q.E.D.
这个定理说明 a 经过编码为 b 再经过解码为 c 时, a == c mod n (n = pq)....
但我们在做编码解码时, 限制 0 <= a < n, 0 <= c < n,
所以这就是说 a 等於 c, 所以这个过程确实能做到编码解码的功能.....
二、RSA 的安全性
RSA的安全性依赖于大数分解,但是否等同于大数分解一直未能得到理论上的证明,因为没有证明破解 RSA就一定需要作大数分解。假设存在一种无须分解大数的算法,那它肯定可以修改成为大数分解算法。目前, RSA 的一些变种算法已被证明等价于大数分解。不管怎样,分解n是最显然的攻击方法。现在,人们已能分解多个十进制位的大素数。因此,模数n 必须选大一些,因具体适用情况而定。
三、RSA的速度
由于进行的都是大数计算,使得RSA最快的情况也比DES慢上倍,无论是软件还是硬件实现。速度一直是RSA的缺陷。一般来说只用于少量数据加密。
四、RSA的选择密文攻击
RSA在选择密文攻击面前很脆弱。一般攻击者是将某一信息作一下伪装( Blind),让拥有私钥的实体签署。然后,经过计算就可得到它所想要的信息。实际上,攻击利用的都是同一个弱点,即存在这样一个事实:乘幂保留了输入的乘法结构:
( XM )^d = X^d *M^d mod n
前面已经提到,这个固有的问题来自于公钥密码系统的最有用的特征--每个人都能使用公钥。但从算法上无法解决这一问题,主要措施有两条:一条是采用好的公钥协议,保证工作过程中实体不对其他实体任意产生的信息解密,不对自己一无所知的信息签名;另一条是决不对陌生人送来的随机文档签名,签名时首先使用One-Way HashFunction 对文档作HASH处理,或同时使用不同的签名算法。在中提到了几种不同类型的攻击方法。
五、RSA的公共模数攻击
若系统中共有一个模数,只是不同的人拥有不同的e和d,系统将是危险的。最普遍的情况是同一信息用不同的公钥加密,这些公钥共模而且互质,那末该信息无需私钥就可得到恢复。设P为信息明文,两个加密密钥为e1和e2,公共模数是n,则:
C1 = P^e1 mod n
C2 = P^e2 mod n
密码分析者知道n、e1、e2、C1和C2,就能得到P。
因为e1和e2互质,故用Euclidean算法能找到r和s,满足:
r * e1 + s * e2 = 1
假设r为负数,需再用Euclidean算法计算C1^(-1),则
( C1^(-1) )^(-r) * C2^s = P mod n
另外,还有其它几种利用公共模数攻击的方法。总之,如果知道给定模数的一对e和d,一是有利于攻击者分解模数,一是有利于攻击者计算出其它成对的e’和d’,而无需分解模数。解决办法只有一个,那就是不要共享模数n。
RSA的小指数攻击。 有一种提高 RSA速度的建议是使公钥e取较小的值,这样会使加密变得易于实现,速度有
所提高。但这样作是不安全的,对付办法就是e和d都取较大的值。
RSA算法是第一个能同时用于加密和数字签名的算法,也易于理解和操作。RSA是被研究得最广泛的公钥算法,从提出到现在已近二十年,经历了各种攻击的考验,逐渐为人们接受,普遍认为是目前最优秀的公钥方案之一。RSA的安全性依赖于大数的因子分解,但并没有从理论上证明破译RSA的难度与大数分解难度等价。即RSA的重大缺陷是无法从理论上把握它的保密性能如何,而且密码学界多数人士倾向于因子分解不是NPC问题。 RSA的缺点主要有:A)产生密钥很麻烦,受到素数产生技术的限制,因而难以做到一次一密。B)分组长度太大,为保证安全性,n 至少也要 600 bits 以上,使运算代价很高,尤其是速度较慢,较对称密码算法慢几个数量级;且随着大数分解技术的发展,这个长度还在增加,不利于数据格式的标准化。目前,SET( Secure Electronic Transaction )协议中要求CA采用比特长的密钥,其他实体使用比特的密钥。