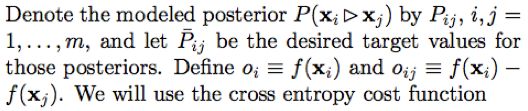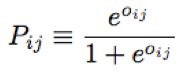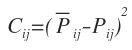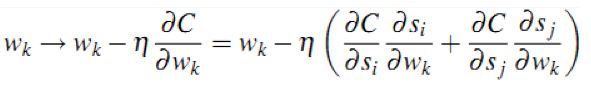排序学习---ranknet方法
1 背景
随着移动互联网的崛起,越来越多的用户开始习惯于从手机完成吃、喝、玩、乐、衣、食、住、行等各个方面的需求。打开手机,点开手淘、美团等APP,商品玲玲满目,而让用户将所有商品一页页看完已经不现实,通常情况下用户也就查看前几页,如果找不到满意的商品则退出,从而造成流单。因此如何对商品进行排序使得用户能尽快完成购买流程已经成为这些平台的重要攻克方向。
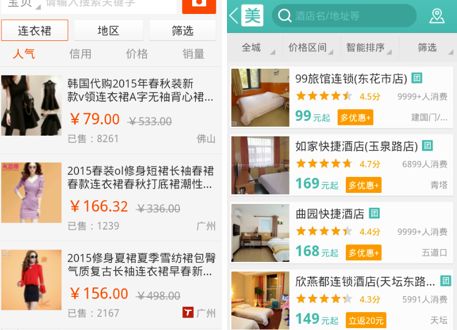
图1 手机淘宝、美团等app的商品排序示意
传统的方法是找几个特征比如评分、销量等,然后找个打分函数如简单的线性函数:F=w1*评分+w2*销量+...,并通过手工调整权重值w并结合abtest实验来达到排序的目的(分数越高排名越高)。
这种方法非常简单,但面临着一些问题:1)每当增加一个特征都得调整所有特征的权重,并在线上进行abtest,费时费力;2)特征较多时(当引入个性化特征时),这种手工调整权重的方式已经不可能完成,很难找到一个较优解;3)随着数据的不断变化,每隔一段时间都需要人工重新调节权重。总体来讲人工调参费时费力、效果也差!
为了避免人工调参,现在工业界主要采用排序学习方法。
2 排序学习简介
排序学习的目的就是通过一些自动化的方法完成模型参数的训练。根据不同类型的训练数据可以将排序学习方法分为以下三类:a)单点标注(point wise);b)两两标注(pair wise);c)列表标注(list wise)。
2.1 point wise过程
下面介绍如何使用point wise方法来完成排序学习。
排序学习最重要的工作就是构造训练样本,即得到一组(V1,V2,V3,..., Y),其中V是特征,Y是label,得到样本之后带入相应的机器学习模型即可完成训练。
一般来说特征可分成以下几类(根据业务不同可自行添加特征):a)商品(文档)本身特征如:评分、销量、价格等;b)用户本身特征如:性别、年龄、用户的商品类型偏好等;c)用户-商品关联特征如:是否看过此商品、是否买过此商品、对此商品的历史评价等;d)场景特征如:时间(早中晚)、与商品的距离、是否是节假日等。
找到特征后需要定义label。我们认为给用户展示过的商品label为1,用户点击过的商品label为3,用户购买过的商品label为7。
通过对历史日志数据的清洗整理我们可以得到成千上万的样本(V1,V2,V3,..., Y)。
得到样本之后我们可以将此排序问题转换为多分类问题(样本特征-类别标记)或者回归问题(样本特征-连续值)。如果转换为多分类问题,我们模型最后的输出只能1、3或是7,往往导致在同一类中的文档(比如两个文档输入模型的得到的结果都是7)不好继续排序,因此实际使用中往往将问题转换为回归问题,常常采用LR、GBDT等来解决。
2.2 point wise缺点
point wise方法很直观,非常容易将问题转换为我们所熟知的问题,但其缺点是完全从单文档的分类角度计算,没有考虑文档之间的相对顺序。
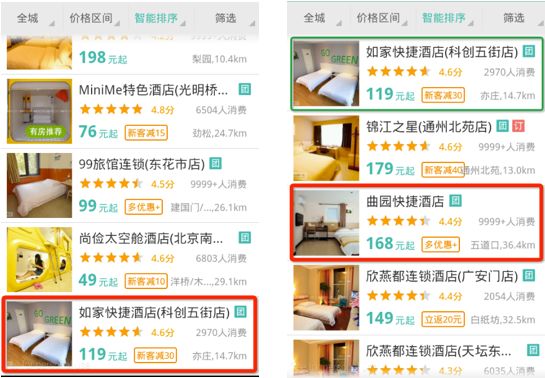
举个例子。假设图2左图红框为某一次用户点击的事件,这时候我们获得一条样本i (V1i,V2i,V3i,...,Xni, 3)。右图红框为某一次用户点击的事件,我们获得一条样本j (V1j,V2j,V3j,...,Vnj, 3)。按照pointwise的思想,我们认为这两条样本的label都是3。但在第二张图包含更重要的信息,“用户只点了红框内的酒店,而没有点绿框内的酒店(绿框内的酒店和左图点击的酒店一致)”,即说明样本j的label应该比样本i的label大(样本j排名比样本i更靠前),而pointwise并没有利用到这个信息。
图2 point wise缺点示意图
自然我们的问题就是:如何将文档之间相对顺序信息利用进去呢?
2.3 pair wise方法
在pairwise方法中,我们不再从从单文档的分类角度来看待问题,而是从一个文档对如
下面我们着重介绍下ranknet的原理以及应用。
3 ranknet
3.1 ranknet原理
假设有文档i和j,其中文档i的特征向量是Xi(1i, v2i, v3i, ..., vni),文档j的特征向量是Xj(v1i, v2j, v3j, ..., vnj),我们要找一个打分函数F,假设F是线性函数,F(Xi)=W*Xi=w1*v1i + w1*v2i + ... + wn*vni,其中w表示权重系数,F(Xi)表示针对文档Xi给出的得分。
我们希望找出这样一个函数F(本质上是训练得到这些权重w),当文档X1比X2排名高时,我们希望F(Xi) > F(Xj)。
下面我们需要定义损失函数了。首先定义概率Pij,用于表示Xi比Xj排名高的概率,直观上可以设Pij=F(Xi)-F(Xj),这样F(Xi)-F(Xj)越大表示Xi比Xj排名高的概率越大,但这里问题的关键是概率值是在[0,1]区间范围内的,因此需要归一化。可以参考逻辑斯蒂回归的归一化函数:
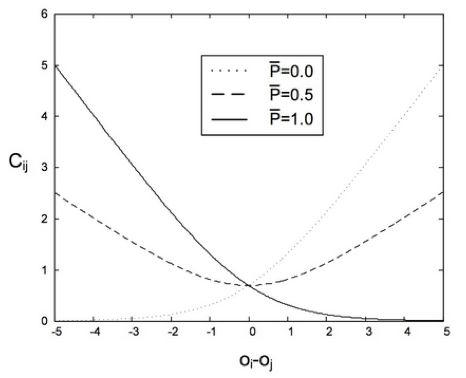
其中Oi=F(i),Oij=F(i)-F(j),这个函数有比较好的特质,当Oij=0时,Pij=0.5,当Oij>0时,Pij>0.5,并且当Oij趋向于无穷大时,Pij=1,反之当Oij<0时,Pij<0.5,当Oij趋向于无穷小时,Pij=0。
这个时候我们就可以定义损失函数了。损失函数常用有两种类型:
1)平方损失函数
这是最常用的损失函数,但是现在由于已经做了归一化逻辑映射,使得平方损失函数不再是一个凸函数,这给我们最优化求解造成了比较大的挑战,因此实际常常使用另一种损失函数---交叉熵。
2)交叉熵
这里插句题外话,为什么非凸函数的最优解不好求?
如下图所示一个非凸函数,要求最小值,我们常使用的梯度下降法或者牛顿迭代法往往限于局部最优解,很难找到全局最优解。
下面看看交叉熵损失函数是否能满足我们的需求。
得到了凸损失函数之后,就可以使用梯度下降方法求解最优化参数。
如果直接这么训练最终得到的是线性模型,不能学习特征之间的非线性关系,一般学习非线性关系有几种方法:1)一种是对特征进行高维映射,例如svm的核方法;2)树模型;3)带有隐藏层的神经网络。
3.2 基于神经网络的ranknet
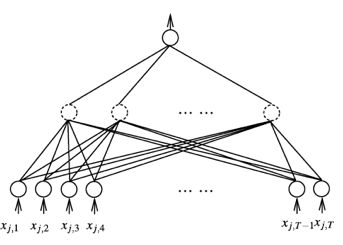
在实际使用中,ranknet采用神经网络方法进行学习,一般采用的是带有隐层的神经网络。学习过程一般使用误差反向传播方法来训练。
这里的输入层(最底部)的神经元代表了样本的每一个特征,虚线的神经元代表隐藏层,最终输出只有一个神经元。
如何训练呢?这里提供了两种思路:
1)取一个样本对(Xi, Xj),首先对Xi带入神经网络进行前向反馈,其次将Xj带入神经网络进行前向反馈,然后计算差分结果并进行误差反向传播,接着取下一个样本对。。。
这种方法很直观,缺点是收敛速度慢。
2)批量训练。我们可以对同一个排序下的所有文档pair全部带入神经网络进行前向反馈,然后计算总差分并进行误差反向传播,这样将大大减少误差反向传播的次数,原理如下公式推导所示。
3.3应用
我们输入的样本如下所示:相应的字段为:
7 qid:1 1:1 2:1 3:0 4:0.2 5:0 # 1A
3 qid:1 1:0 2:0 3:1 4:0.1 5:1 # 1B
1 qid:1 1:0 2:1 3:0 4:0.4 5:0 # 1C
1 qid:1 1:0 2:0 3:1 4:0.3 5:0 # 1D
1 qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2A
3 qid:2 1:1 2:0 3:1 4:0.4 5:0 # 2B
1 qid:2 1:0 2:0 3:1 4:0.1 5:0 # 2C
1 qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2D
1 qid:3 1:0 2:0 3:1 4:0.1 5:1 # 3A
3 qid:3 1:1 2:1 3:0 4:0.3 5:0 # 3B
7 qid:3 1:1 2:0 3:0 4:0.4 5:1 # 3C
1 qid:3 1:0 2:1 3:1 4:0.5 5:0 # 3D
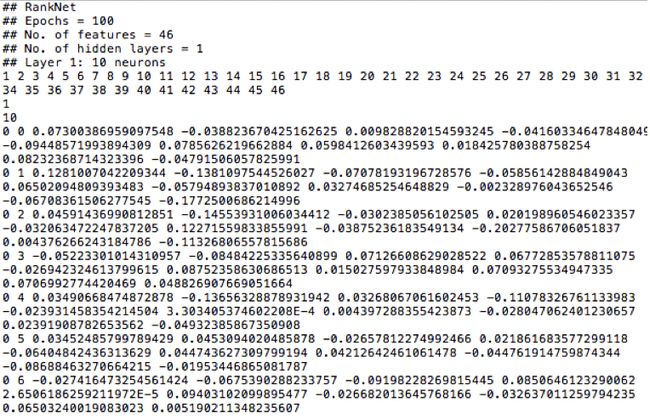
将样本输入到ranknet进行训练,最终得到如下所示结果,其中我们特征为46个,即输入层中神经元个数为46个,隐藏层只设置了1层,隐藏层神经元个数设置为10个。
得到模型结果后,将此模型保存到缓存中。假设来一个线上请求,我们首先提取出各个文档的特征向量(V1, V2, V3, ..., Vn),带入此神经网络模型得到各个文档的评分,并按照评分进行排序。
转自http://www.cnblogs.com/LBSer/p/4439542.html