生成性对抗网络及其变体的工作原理:GAN概述
生成性对抗网络及其变体的工作原理:GAN概述
- GAN的基本介绍
- GAN的基本概念
- 目标函数
- f-divergence[f-散度]
- Integral probality metric(IPM,可积概率度量)
- f-divergence 和 IPM 对比
- 辅助的目标函数
- 其他常见生成式模型
- 自回归模型:pixelRNN与pixelCNN
- VAE
- GAN常见的模型结构
- DCGAN
- 层级结构
- 自编码结构
- GAN的训练障碍
- 理论中存在的问题
- 实践中存在的问题
- 稳定GAN训练的技巧
- mode collapse的解决方案
- 针对目标函数的改进方法
- 针对网络结构的改进方法
- Mini-batch Discrimination
- 关于GAN隐空间的理解
- 隐空间分解
- 有监督方法
- 无监督方法
- GAN与VAE的结合
- GAN模型总结
- GAN的应用
- 图像
- 图像翻译
- 超分辨
- 目标检测
- 图像联合分布学习
- 视频生成
- 序列生成
- 音乐生成
- 语言和语音
- 半监督学习
- 利用判别器进行半监督学习
- 使用辅助分类器的半监督学习
- 域适应
- 其他应用
- 医学图像分割
- 图片隐写
- 连续学习
- 讨论
- GAN的评价
- Inception Score
- Mode Score
- Kernel MMD(Maximum Mean Discrepancy)
- Wasserstein Distance
- Fréchet Inception Distance (FID)
- 1-Nearest Neighbor classifier
- 其他评价方法
- 总结
- GAN与强化学习的关系
- GAN的优缺点
- 优点
- 缺点
- 未来的研究方向
最近发现有一篇最新的 GAN 综述论文,四十余页,介绍了 GAN 的各个方面,于是就学习并整理笔记如下。有学者以及翻译整理,本人将其整理转发与CSDN中仅学习和分享。本博客参考;若有不当,请联系本人。
这篇综述主要参考最新的一篇有关GAN综述的paper1,详细探讨了GAN的各种细节,以及改进,应用。本文对于论文内容做了一些调整以及补充,方便入门的同学阅读。目录如下:
GAN的基本介绍
生成对抗网络(GAN , Generative Adversarial Networks)作为一种优秀的生成式模型,引爆了许多图像生成的有趣应用。GAN相比于其他生成式模型,有两大特点:
- 不依赖任何先验假设。传统的许多方法会假设数据服从某一分布,然后使用极大似然去估计数据分布。
- 生成real-like样本的方式非常简单。GAN生成real-like样本的方式通过生成器(Generator)的前向传播,而传统方法的采样方式非常复杂,有兴趣的同学可以参考下周志华老师的《机器学习》一书中对各种采样方式的介绍。
下面,我们围绕上述两点展开介绍。
GAN的基本概念
GAN (Generative Adversarial Networks)从其名字可以看出,是一种生成式的,对抗网络。再具体一点,就是通过对抗的方式,去学习数据分布的生成式模型。所谓的对抗,指的是生成网络和判别网络的互相对抗。生成网络尽可能生成逼真样本,判别网络则尽可能去判别该样本是真实样本,还是生成的假样本。示意图如下:
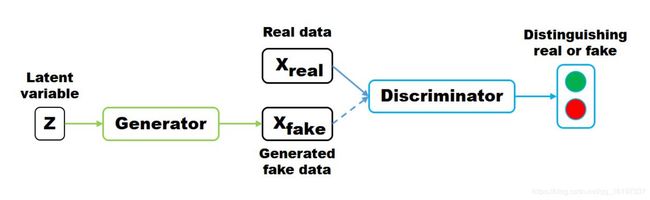
隐变量 z z z (通常为服从高斯分布的随机噪声)通过Generator生成 X f a k e X_{fake} Xfake ,判别器负责判别输入的data是生成的样本 X f a k e X_{fake} Xfake还是真实的样本 X r e a l X_{real} Xreal 。优化的目标函数如下:
min G max D V ( D , G ) = min G max D E x ∼ P d a t a ( x ) [ log D ( x ) ] + E z ∼ p z ( z ) [ log ( 1 − D ( G ( Z ) ) ) ] \min_G \max_D V( D,G) = \min_G \max_D \mathbf{E}_{x \sim P_{data}(x)}[\log D(x)]+ \mathbf{E}_{z \sim p_z(z)}[\log(1-D(G(Z)))] GminDmaxV(D,G)=GminDmaxEx∼Pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(Z)))]
对于判别器 D D D 来说,这是一个二分类问题, V ( D , G ) V(D,G) V(D,G) 为二分类问题中常见的交叉熵损失。对于生成器 G G G 来说,为了尽可能欺骗 D D D,所以需要最大化生成样本的判别概率 D ( G ( z ) ) D(G(z)) D(G(z)),即最小化 log ( 1 − D ( G ( z ) ) ) \log(1-D(G(z))) log(1−D(G(z))),注意: log ( D ( x ) ) \log(D(x)) log(D(x)) 一项与生成器 G G G 无关,所以可以忽略。
实际训练时,生成器和判别器采取交替训练,即先训练 D D D,然后训练 G G G,不断往复。值得注意的是,对于生成器,其最小化的是 max D V ( D , G ) \max \limits_D V(D,G) DmaxV(D,G),即最小化 V ( D , G ) V(D,G) V(D,G) 的最大值。
为了保证 V ( D , G ) V(D,G) V(D,G) 取得最大值,所以我们通常会训练迭代k次判别器,然后再迭代1次生成器(不过在实践当中发现,k 通常取 1 即可)。当生成器 G G G 固定时,我们可以对 V ( D , G ) V(D,G) V(D,G) 求导,求出最优判别器 D ∗ ( x ) D^*(x) D∗(x):
D ∗ ( x ) = p g ( x ) p g ( x ) + p d a t a ( x ) D^*(x) = \frac{p_g(x)}{p_g(x)+p_{data}(x)} D∗(x)=pg(x)+pdata(x)pg(x)
把最优判别器代入上述目标函数,可以进一步求出在最优判别器下,生成器的目标函数等价于优化 P d a t a ( x ) P_{data}(x) Pdata(x) , P g ( x ) P_g(x) Pg(x) 的 J S JS JS 散度(JSD, Jenson Shannon Divergence)。
可以证明,当 G G G, D D D 二者的 capacity 足够时,模型会收敛,二者将达到纳什均衡。此时, P d a t a ( x ) = P g ( x ) P_{data}(x)=P_g(x) Pdata(x)=Pg(x),判别器不论是对于 P d a t a ( x ) P_{data}(x) Pdata(x) 还是 P g ( x ) P_g(x) Pg(x) 中采样的样本,其预测概率均为 1 2 \frac{\bm 1}{\bm 2} 21,即生成样本与真实样本达到了难以区分的地步。
目标函数
前面我们提到了GAN的目标函数是最小化两个分布的Js散度。实际上,衡量两个分布距离的方式有很多种,Js散度只是其中一种。如果我们定义不同的距离度量方式,就可以得到不同的目标函数。许多对GAN训练稳定性的改进,比如EBGAN, LSGAN等都是定义了不同的分布之间距离度量方式。
f-divergence[f-散度]
f-divergence使用下面公式来定义连个分布之间的距离:
D f ( p d a t a ∣ ∣ p g ) = ∫ x p g ( x ) f ( p d a t a ( x ) p g ( x ) ) d x D_f(p_data||p_g) = \int_x p_g(x)f(\frac{p_{data}(x)}{p_g(x)})dx Df(pdata∣∣pg)=∫xpg(x)f(pg(x)pdata(x))dx
上述公式中 f f f为凸函数,且 f ( 1 ) = 0 f(1)=0 f(1)=0。采用不同的 f f f函数(Generator),可以得到不同的优化目标。具体如下:

值得注意的是,散度这种度量方式不具备对称性,即 D f ( P d a t a ∣ ∣ P g ) D_f(P_{data}||P_g) Df(Pdata∣∣Pg) 和 D f ( P g ∣ ∣ P d a t a ) D_f(P_g||P_{data}) Df(Pg∣∣Pdata)不相等。
LSGAN
上面提到,LSGAN 是 f-divergence 中 f ( x ) = ( t − 1 ) 2 f(x)=(t-1)^2 f(x)=(t−1)2时的特殊情况。具体来说 LSGAN 的 Loss 如下:
min D J ( D ) = min D [ 1 2 E x ∼ p d a t a ( x ) [ D ( x ) − a ] 2 + 1 2 E z ∼ p z ( x ) [ D ( G ( z ) ) − b ] 2 ] \min_D J(D) = \min_D [\frac{1}{2} \mathbf E_{x\sim p_{data}(x)}[D(x)-a]^2+\frac{1}{2} \mathbf E_{z\sim p_z(x)}[D(G(z))-b]^2] DminJ(D)=Dmin[21Ex∼pdata(x)[D(x)−a]2+21Ez∼pz(x)[D(G(z))−b]2]
原作中取 a = c = 1 , b = 0 a=c=1,b=0 a=c=1,b=0。LSGAN 有两大优点:
稳定训练:解决了传统GAN训练过程中的梯度饱和问题
改善生成质量:通过惩罚远离判别器决策边界的生成样本来实现
对于第一点,稳定训练,可以先看一张图:
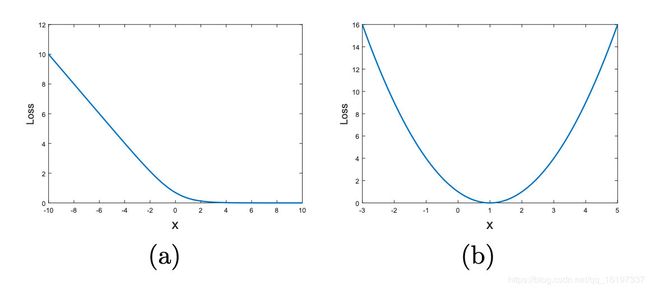
上图左边是传统 GAN 使用 sigmoid 交叉熵作为 loss 时,输入与输出的对照关系图。上图右边是 LSGAN 使用最小二乘 loss 时,输入与输出的对照关系图。可以看到,在左图,输入比较大的时候,梯度为 0,即交叉熵损失的输入容易出现梯度饱和现象。而右边的最小二乘 loss 则不然。
对于第二点,改善生成质量。这个在原文也有详细的解释。具体来说:对于一些被判别器分类正确的样本,其对梯度是没有贡献的。但是判别器分类正确的样本就一定是很接近真实数据分布的样本吗?显然不一定。
考虑如下理想情况,一个训练良好的 GAN,真实数据分布 P d a t a P_{data} Pdata 和生成数据分布 P g P_g Pg 完全重合,判别器决策面穿过真实数据点,所以,反过来,我们利用样本点离决策面的远近来度量生成样本的质量,样本离决策面越近,则 GAN 训练的越好。
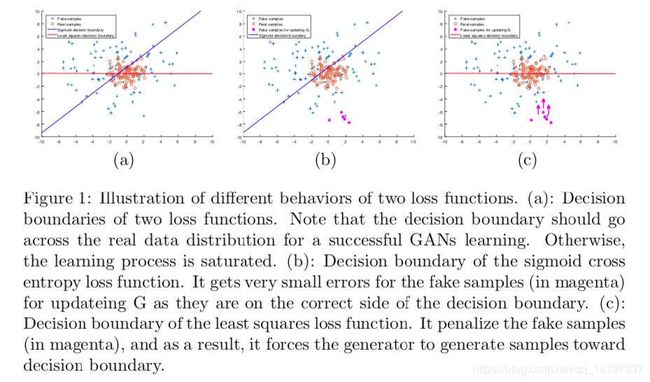
上图 b 中,一些离决策面比较远的点,虽然被分类正确,但是这些并不是好的生成样本。传统 GAN 通常会将其忽略。而对于 LSGAN,由于采用最小二乘损失,计算决策面到样本点的距离,如图 c,可以把离决策面比较远的点“拉”回来,也就是把离真实数据比较远的点“拉”回来。
Integral probality metric(IPM,可积概率度量)
IPM 定义了一个评价函数 f \bm f f,用于度量任意两个分布之间的距离。在一个紧凑的空间中 χ ⊂ R d \chi \subset \mathcal R^d χ⊂Rd,定义 P ( χ ) P(\chi) P(χ) 为在 x \bm x x 上的概率测度。那么两个分布 P d a t a P_{data} Pdata, P g P_g Pg 之间的 IPM 可以定义为如下公式:
d F ( p d a t a , p g ) = s u p f ∈ F E x ∼ p d a t a [ f ( x ) ] − E x ∼ p d a t a [ f ( x ) ] d_{\mathcal F}(p_{data},p_g)=sup_{f\in \mathcal F} \mathbf E_{x \sim p_{data}}[f(x)]-\mathbf E_{x \sim p_{data}}[f(x)] dF(pdata,pg)=supf∈FEx∼pdata[f(x)]−Ex∼pdata[f(x)]
类似于 f-divergence,不同函数 f f f 也可以定义出一系列不同的优化目标。典型的有 WGAN,Fisher GAN 等。下面简要介绍一下 WGAN。
WGAN
WGAN 提出了一种全新的距离度量方式——地球移动距离(EM, Earth-mover distance),也叫 Wasserstein 距离。关于 Wasserstein 距离的介绍可以参考:白话 Wassertein 距离 :
Wasserstein 距离具体定义如下:
W ( p d a t a , p g ) = i n f γ ∈ ⊓ ( p d a t a , p g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] W(p_{data},p_g) = inf_{\gamma \in \sqcap (p_{data},p_g)} \mathbf E_{(x,y) \sim \gamma} [\| x-y \|] W(pdata,pg)=infγ∈⊓(pdata,pg)E(x,y)∼γ[∥x−y∥]
⊓ ( p d a t a , p g ) \sqcap (p_{data},p_g) ⊓(pdata,pg) 表示一组联合分布,这组联合分布里的任一分布 γ \gamma γ 的边缘分布均为 p d a t a ( x ) p_{data}(x) pdata(x) 和 p g ( x ) p_g(x) pg(x)。
直观上来说,概率分布函数(PDF)可以理解为随机变量在每一点的质量,所以 W ( p d a t a , p g ) W(p_{data},p_g) W(pdata,pg) 则表示把概率分布 p d a t a ( x ) p_{data}(x) pdata(x) 搬到 p g ( x ) p_g(x) pg(x) 需要的最小工作量。
WGAN 也可以用最优传输理论来解释,WGAN 的生成器等价于求解最优传输映射,判别器等价于计算 Wasserstein 距离,即最优传输总代价 。关于 WGAN 的理论推导和解释比较复杂,不过代码实现非常简单。具体来说 :
- 判别器最后一层去掉 sigmoid
- 生成器和判别器的 loss 不取 log \log log
- 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数 c
上述第三点,在 WGAN 的后来一篇工作 WGAN-GP 中,将梯度截断替换为了梯度惩罚。
f-divergence 和 IPM 对比
- f-divergence 存在两个问题:其一是随着数据空间的维度 x ∈ χ = R d \bm x \in \chi = \mathcal R^d x∈χ=Rd的增加,f-divergence 会非常难以计算。其二是两个分布的支撑集通常是未对齐的,这将导致散度值趋近于无穷。
IPM 则不受数据维度的影响,且一致收敛于 p d a t a p_{data} pdata, p g p_g pg 两个分布之间的距离。而且即便是在两个分布的支撑集不存在重合时,也不会发散。
辅助的目标函数
在许多 GAN 的应用中,会使用额外的 Loss 用于稳定训练或者达到其他的目的。比如在图像翻译,图像修复,超分辨当中,生成器会加入目标图像作为监督信息。EBGAN 则把 GAN 的判别器作为一个能量函数,在判别器中加入重构误差。CGAN 则使用类别标签信息作为监督信息。
其他常见生成式模型
自回归模型:pixelRNN与pixelCNN
自回归模型通过对图像数据的概率分布 p d a t a p_{data} pdata进行显式建模,并利用极大似然估计优化模型。具体如下:
p d a t a ( x ) = ∏ i = 1 n p ( x i ∣ x 1 , x 2 , . . . , x i − 1 ) p_{data}(x) = \prod _{i=1}^n p(x_i | x_1,x_2, ...,x_{i-1}) pdata(x)=i=1∏np(xi∣x1,x2,...,xi−1)
上述公式很好理解,给定 x 1 , x 2 , . . . , x i − 1 x_1,x_2,...,x_{i-1} x1,x2,...,xi−1 条件下,所有 p ( x i ) p(x_i) p(xi) 的概率乘起来就是图像数据的分布。如果使用 RNN 对上述依然关系建模,就是 pixelRNN。如果使用 CNN,则是 pixelCNN。具体如下:
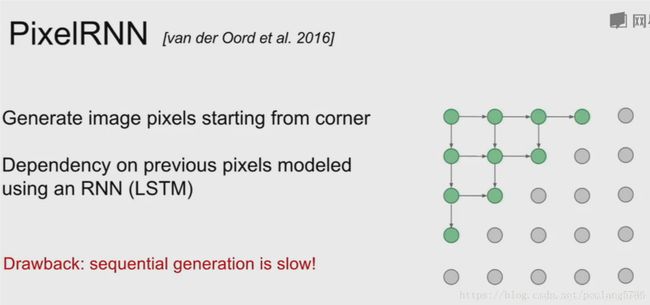
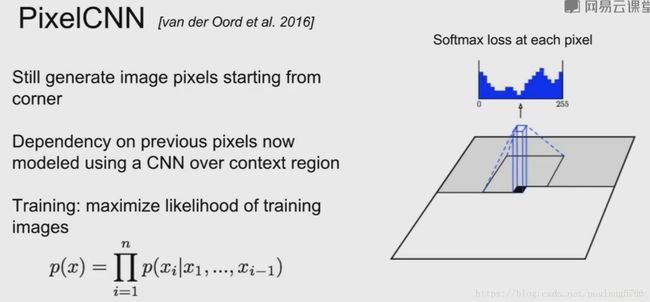
显然,不论是对于 pixelCNN 还是 pixelRNN,由于其像素值是一个个生成的,速度会很慢。语音领域大火的 WaveNet 就是一个典型的自回归模型。
VAE
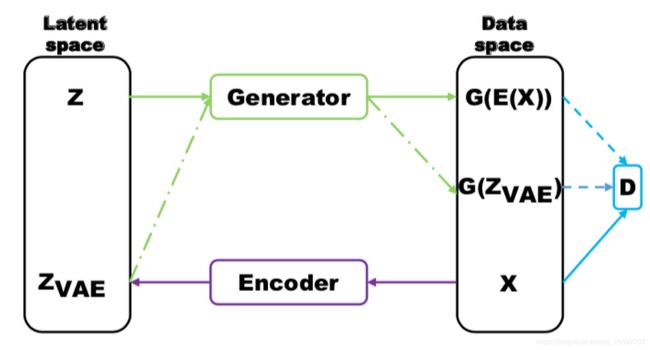
PixelCNN/RNN 定义了一个易于处理的密度函数,我们可以直接优化训练数据的似然;对于变分自编码器我们将定义一个不易处理的密度函数,通过附加的隐变量 z \bm z z 对密度函数进行建模。VAE 原理图如下 :
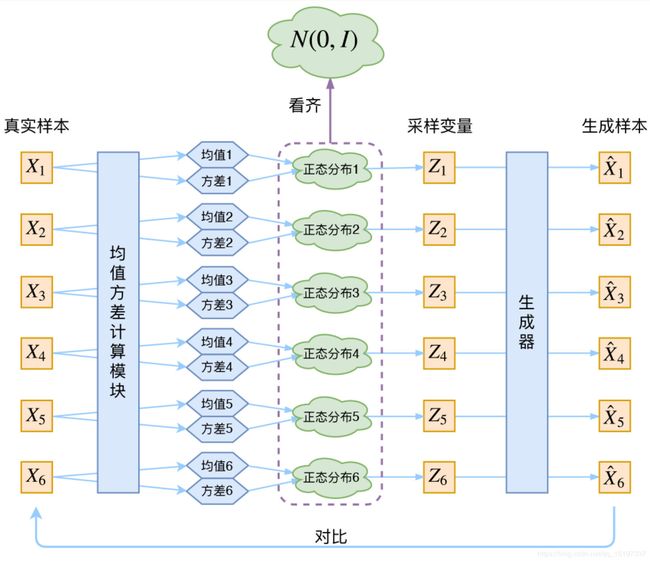
在 VAE 中,真实样本X通过神经网络计算出均值方差(假设隐变量服从正态分布),然后通过采样得到采样变量 Z 并进行重构。VAE 和 GAN 均是学习了隐变量 z \bm z z 到真实数据分布的映射。但是和 GAN 不同的是:
- GAN 的思路比较粗暴,使用一个判别器去度量分布转换模块(即生成器)生成分布与真实数据分布的距离。
- VAE 则没有那么直观,VAE 通过约束隐变量 z 服从标准正态分布以及重构数据实现了分布转换映射 X = G ( z ) X=G(z) X=G(z)。
生成式模型对比
- 自回归模型通过对概率分布显式建模来生成数据; VAE 和 GAN 均是:
- 假设隐变量 z 服从某种分布,并学习一个映射 X=G(z),实现隐变量分布 z 与真实数据分布 p d a t a ( x ) p_{data}(x) pdata(x) 的转换;
- GAN 使用判别器去度量映射 X=G(z) 的优劣,而 VAE通过隐变量 z 与标准正态分布的 KL 散度和重构误差去度量。
GAN常见的模型结构
DCGAN
DCGAN 提出使用 CNN 结构来稳定 GAN 的训练,并使用了以下一些 trick:
- Batch Normalization
- 使用 Transpose convlution 进行上采样
- 使用 Leaky ReLu 作为激活函数
上面这些 trick 对于稳定 GAN 的训练有许多帮助,自己设计 GAN 网络时也可以酌情使用。
层级结构
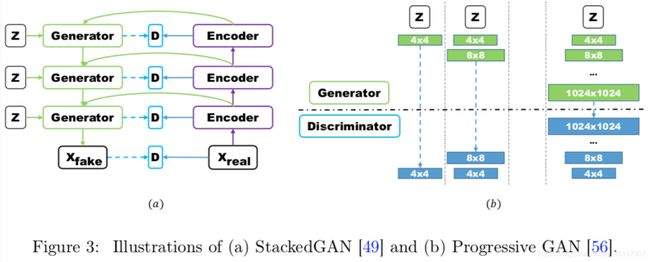
GAN 对于高分辨率图像生成一直存在许多问题,层级结构的 GAN 通过逐层次,分阶段生成,一步步提生图像的分辨率。典型的使用多对 GAN 的模型有StackGAN,GoGAN。使用单一 GAN,分阶段生成的有 ProgressiveGAN。StackGAN 和 ProgressiveGAN 结构如下:
自编码结构
经典的 GAN 结构里面,判别网络通常被当做一种用于区分真实/生成样本的概率模型。而在自编码器结构里面,判别器(使用 AE 作为判别器)通常被当做能量函数(Energy function)。对于离数据流形空间比较近的样本,其能量较小,反之则大。有了这种距离度量方式,自然就可以使用判别器去指导生成器的学习。
AE 作为判别器,为什么就可以当做能量函数,用于度量生成样本离数据流形空间的距离呢?首先,先看 AE 的 loss:
D ( u ) = ∥ u − A E ( u ) ∥ D(u) = \| u-AE(u) \| D(u)=∥u−AE(u)∥
AE 的 loss 是一个重构误差。使用 AE 做为判别器时,如果输入真实样本,其重构误差会很小。如果输入生成的样本,其重构误差会很大。因为对于生成的样本,AE 很难学习到一个图像的压缩表示(即生成的样本离数据流行形空间很远)。所以,VAE 的重构误差作为 p d a t a p_{data} pdata 和 p g p_g pg 之间的距离度量是合理的。典型的自编码器结构的 GAN 有:BEGAN,EBGAN,MAGAN 等。
GAN的训练障碍
理论中存在的问题
经典 GAN 的判别器有两种 loss,分别是:
E x ∼ p g [ l o g ( 1 − D ( x ) ] E x ∼ p g [ − l o g ( D ( x ) ] E_{x \sim p_g} [log(1-D(x)] \\ E_{x \sim p_g} [-log(D(x)] Ex∼pg[log(1−D(x)]Ex∼pg[−log(D(x)]
使用上面第一个公式作为 loss 时:在判别器达到最优的时候,等价于最小化生成分布与真实分布之间的 JS 散度,由于随机生成分布很难与真实分布有不可忽略的重叠以及 JS 散度的突变特性,使得生成器面临梯度消失的问题。
使用上面第二个公式作为 loss 时:在最优判别器下,等价于既要最小化生成分布与真实分布直接的 KL 散度,又要最大化其 JS 散度,相互矛盾,导致梯度不稳定,而且 KL 散度的不对称性使得生成器宁可丧失多样性也不愿丧失准确性,导致 collapse mode 现象 。
实践中存在的问题
GAN 在实践中存在两个问题:
其一,GAN 提出者 Ian Goodfellow 在理论中虽然证明了 GAN 是可以达到纳什均衡的。可是我们在实际实现中,我们是在参数空间优化,而非函数空间,这导致理论上的保证在实践中是不成立的。
其二,GAN 的优化目标是一个极小极大(minmax)问题,即 min G max D V ( G , D ) \min \limits_G \max \limits_D V(G,D) GminDmaxV(G,D),也就是说,优化生成器的时候,最小化的是 max D V ( G , D ) \max \limits_D V(G,D) DmaxV(G,D)。可是我们是迭代优化的,要保证 V ( G , D ) V(G,D) V(G,D) 最大化,就需要迭代非常多次,这就导致训练时间很长。
如果我们只迭代一次判别器,然后迭代一次生成器,不断循环迭代。这样原先的极小极大问题,就容易变成极大极小(maxmin)问题,可二者是不一样的,即:
min G max D V ( G , D ) = ≠ max D min G V ( G , D ) \min_G \max _D V(G,D) = \neq \max _D \min_G V(G,D) GminDmaxV(G,D)≠=DmaxGminV(G,D)
如果变化为极小极大问题,那么迭代就是这样的,生成器先生成一些样本,然后判别器给出错误的判别结果并惩罚生成器,于是生成器调整生成的概率分布。可是这样往往导致生成器变“懒”,只生成一些简单的,重复的样本,即缺乏多样性,也叫 mode collapse。
稳定GAN训练的技巧
如上所述,GAN 在理论上和实践上存在三个大问题,导致训练过程十分不稳定,且存在 mode collapse 的问题。为了改善上述情况,可以使用以下技巧稳定训练:
- Feature matching:方法很简单,使用判别器某一层的特征替换原始 GAN Loss 中的输出。即最小化:生成图片通过判别器的特征和真实图片通过判别器得到的特征之间的距离。
- 标签平滑:GAN 训练中的标签非 0 即 1,这使得判别器预测出来的 confidence 倾向于更高的值。使用标签平滑可以缓解该问题。具体来说,就是把标签 1 替换为 0.8~1.0 之间的随机数。
- 谱归一化:WGAN 和 Improve WGAN 通过施加 Lipschitz 条件来约束优化过程,谱归一化则是对判别器的每一层都施加 Lipschitz 约束,但是谱归一化相比于 Improve WGAN 计算效率要高一些。
- PatchGAN:准确来说 PatchGAN 并不是用于稳定训练,但这个技术被广泛用于图像翻译当中,PatchGAN 相当于对图像的每一个小 Patch 进行判别,这样可以使得生成器生成更加锐利清晰的边缘。
具体做法是这样的:假设输入一张 256x256 的图像到判别器,输出的是一个 4x4 的 confidence map,confidence map 中每一个像素值代表当前 patch 是真实图像的置信度,即为 PatchGAN。当前图像 patch 的大小就是感受野的大小,最后将所有 Patch 的 Loss 求平均作为最终的 Loss。
mode collapse的解决方案
针对目标函数的改进方法
为了避免前面提到的由于优化 maxmin 导致 mode 跳来跳去的问题,UnrolledGAN 采用修改生成器 loss 来解决。具体而言,UnrolledGAN 在更新生成器时更新 k 次生成器,参考的 Loss 不是某一次的 loss,是判别器后面 k 次迭代的 loss。注意,判别器后面 k 次迭代不更新自己的参数,只计算 loss 用于更新生成器。这种方式使得生成器考虑到了后面 k 次判别器的变化情况,避免在不同 mode 之间切换导致的模式崩溃问题。此处务必和迭代 k 次生成器,然后迭代 1 次判别器区分开。DRAGAN 则引入博弈论中的无后悔算法,改造其 loss 以解决 mode collapse问题。前文所述的 EBGAN 则是加入 VAE 的重构误差以解决 mode collapse。
针对网络结构的改进方法
Multi agent diverse GAN (MAD-GAN) 采用多个生成器,一个判别器以保障样本生成的多样性。具体结构如下:
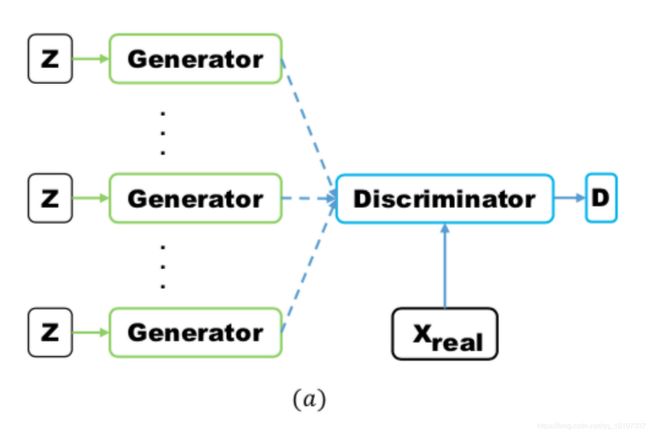
相比于普通 GAN,多了几个生成器,且在 loss 设计的时候,加入一个正则项。正则项使用余弦距离惩罚三个生成器生成样本的一致性。
MRGAN 则添加了一个判别器来惩罚生成样本的 mode collapse 问题。具体结构如下:
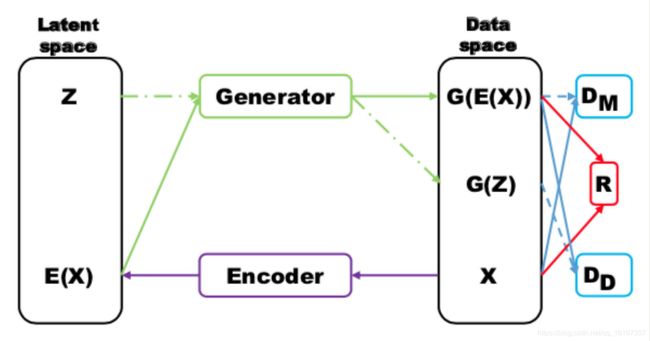
输入样本 x 通过一个 Encoder 编码为隐变量 E(x) ,然后隐变量被 Generator 重构,训练时,Loss 有三个。 D M D_M DM 和 R R R(重构误差)用于指导生成 real-like 的样本。而 D D D_D DD则对 E ( x ) E(x) E(x) 和 z 生成的样本进行判别,显然二者生成样本都是 fake samples,所以这个判别器主要用于判断生成的样本是否具有多样性,即是否出现 mode collapse。
Mini-batch Discrimination
Mini-batch discrimination 在判别器的中间层建立一个 mini-batch layer 用于计算基于 L1 距离的样本统计量,通过建立该统计量去判别一个 batch 内某个样本与其他样本有多接近。这个信息可以被判别器利用到,从而甄别出哪些缺乏多样性的样本。对生成器而言,则要试图生成具有多样性的样本。
关于GAN隐空间的理解
隐空间是数据的一种压缩表示的空间。通常来说,我们直接在数据空间对图像进行修改是不现实的,因为图像属性位于高维空间中的流形中。但是在隐空间,由于每一个隐变量代表了某个具体的属性,所以这是可行的。
在这部分,我们会探讨 GAN 是如何处理隐空间及其属性的,此外还将探讨变分方法如何结合到 GAN 的框架中。
隐空间分解
GAN 的输入隐变量 z 是非结构化的,我们不知道隐变量中的每一位数分别控制着什么属性。因此有学者提出,将隐变量分解为一个条件变量 c 和标准输入隐变量 z 。具体包括有监督的方法和无监督的方法。
有监督方法
典型的有监督方法有 CGAN 和 ACGAN。
CGAN 将随机噪声 z 和类别标签 c 作为生成器的输入,判别器则将生成的样本/真实样本与类别标签作为输入。以此学习标签和图片之间的关联性。
ACGAN 将随机噪声 z 和类别标签 c 作为生成器的输入,判别器则将生成的样本/真实样本输入,且回归出图片的类别标签。以此学习标签和图片之间的关联性。二者结构如下(左边为 CGAN,右边为 ACGAN):
无监督方法
相比于有监督方法,无监督方法不使用任何标签信息。因此,无监督方法需要对隐空间进行解耦得到有意义的特征表示。
InfoGAN 对把输入噪声分解为隐变量 z 和条件变量 c (训练时,条件变量 c 从均匀分布采样而来),二者被一起送入生成器。在训练过程中通过最大化 c 和 G ( z , c ) G(z,c) G(z,c)的互信息 I ( c ; G ( z , c ) ) I(c;G(z,c)) I(c;G(z,c)) 以实现变量解耦( I ( c ; G ( z , c ) I(c;G(z,c) I(c;G(z,c)) 的互信息表示 c 里面关于 G ( z , c ) G(z,c) G(z,c) 的信息有多少,如果最大化互信息 I ( c ; G ( z , c ) ) I(c;G(z,c)) I(c;G(z,c)) ,也就是最大化生成结果和条件变量 c 的关联性)。模型结构和 CGAN 基本一致,除了 Loss 多了一项最大互信息。具体如下 :
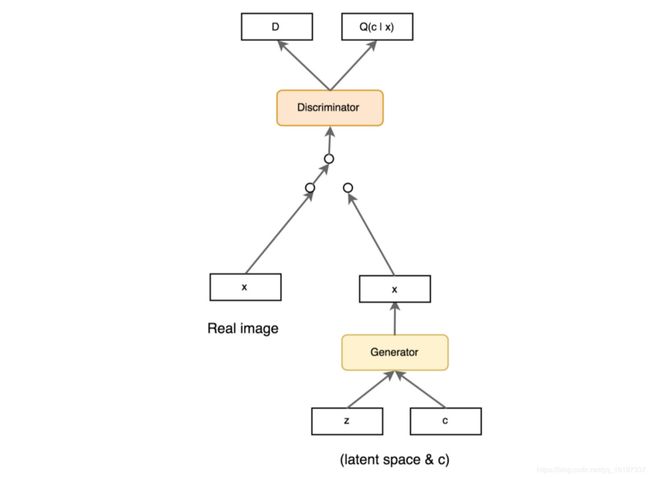
从上面分析可以看出,InfoGAN 只是实现了信息的解耦,至于条件变量 c 每一个值的具体含义是什么,我们无法控制。于是 ss-InfoGAN 出现了,ss-InfoGAN 采用半监督学习方法,把条件变量 c 分成两部分, c = c s s ∩ c u s c=c_{ss}\cap c_{us} c=css∩cus。 c s s c_{ss} css 则利用标签像 CGAN 一样学习, C u s C_{us} Cus 则像 InfoGAN 一样学习。
GAN与VAE的结合
GAN 相比于 VAE 可以生成清晰的图像,但是却容易出现 mode collapse 问题。VAE 由于鼓励重构所有样本,所以不会出现 mode collapse 问题。
一个典型结合二者的工作是 VAEGAN,结构很像前文提及的 MRGAN,具体如下:
上述模型的 Loss 包括三个部分,分别是判别器某一层特征的重构误差,VAE 的 Loss,GAN 的 Loss。
GAN模型总结
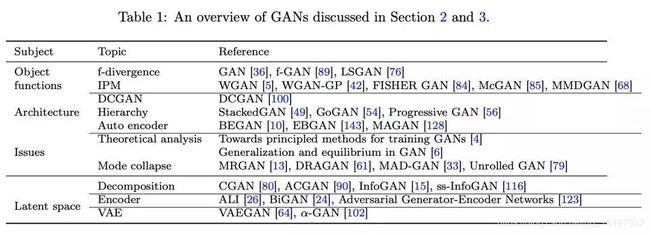
前面两节介绍了各种各样的 GAN 模型,这些模型大都是围绕着 GAN 的两大常见问题:模式崩溃,以及训练崩溃来设计的。下表总结了这些模型,读者可以根据下表回顾对照:
GAN的应用
由于 GAN 在生成样本过程成不需要显式建模任何数据分布就可以生成 real-like 的样本,所以 GAN 在图像,文本,语音等诸多领域都有广泛的应用。下表总结了 GAN 在各个方面的应用,后文会这些算法做相应介绍。
图像
图像翻译
所谓图像翻译,指从一副(源域)图像到另一副(目标域)图像的转换。可以类比机器翻译,一种语言转换为另一种语言。翻译过程中会保持源域图像内容不变,但是风格或者一些其他属性变成目标域。
Paired two domain data
成对图像翻译典型的例子就是 pix2pix,pix2pix 使用成对数据训练了一个条件 GAN,Loss 包括 GAN 的 loss 和逐像素差 loss。而 PAN 则使用特征图上的逐像素差作为感知损失替代图片上的逐像素差,以生成人眼感知上更加接近源域的图像。
Unpaired two domain data
对于无成对训练数据的图像翻译问题,一个典型的例子是 CycleGAN。CycleGAN 使用两对 GAN,将源域数据通过一个 GAN 网络转换到目标域之后,再使用另一个 GAN 网络将目标域数据转换回源域,转换回来的数据和源域数据正好是成对的,构成监督信息。
超分辨
SRGAN 中使用 GAN 和感知损失生成细节丰富的图像。感知损失重点关注中间特征层的误差,而不是输出结果的逐像素误差。避免了生成的高分辨图像缺乏纹理细节信息问题。
目标检测
得益于 GAN 在超分辨中的应用,针对小目标检测问题,可以理由 GAN 生成小目标的高分辨率图像从而提高目标检测精度。
图像联合分布学习
大部分 GAN 都是学习单一域的数据分布,CoupledGAN 则提出一种部分权重共享的网络,使用无监督方法来学习多个域图像的联合分布。具体结构如下:

如上图所示,CoupledGAN 使用两个 GAN 网络。生成器前半部分权重共享,目的在于编码两个域高层的,共有信息,后半部分没有进行共享,则是为了各自编码各自域的数据。判别器前半部分不共享,后半部分用于提取高层特征共享二者权重。对于训练好的网络,输入一个随机噪声,输出两张不同域的图片。
值得注意的是,上述模型学习的是联合分布 P(x,y) ,如果使用两个单独的 GAN 分别取训练,那么学习到的就是边际分布 P(x) 和 P(y)。通常情况下, P(x,y)≠P(x)·P(y) 。
视频生成
通常来说,视频有相对静止的背景和运动的前景组成。VideoGAN 使用一个两阶段的生成器,3D CNN 生成器生成运动前景,2D CNN 生成器生成静止的背景。Pose GAN 则使用 VAE 和 GAN 生成视频,首先,VAE 结合当前帧的姿态和过去的姿态特征预测下一帧的运动信息,然后 3D CNN 使用运动信息生成后续视频帧。Motion and Content GAN (MoCoGAN) 则提出在隐空间对运动部分和内容部分进行分离,使用 RNN 去建模运动部分。
序列生成
相比于 GAN 在图像领域的应用,GAN 在文本,语音领域的应用要少很多。主要原因有两个:
- GAN 在优化的时候使用 BP 算法,对于文本,语音这种离散数据,GAN 没法直接跳到目标值,只能根据梯度一步步靠近。
- 对于序列生成问题,每生成一个单词,我们就需要判断这个序列是否合理,可是 GAN 里面的判别器是没法做到的。除非我们针对每一个 step 都设置一个判别器,这显然不合理。
为了解决上述问题,强化学习中的策略梯度下降(Policy gredient descent)被引入到 GAN 中的序列生成问题。
音乐生成
RNN-GAN 使用 LSTM 作为生成器和判别器,直接生成整个音频序列。然而,正如上面提到的,音乐当做包括歌词和音符,对于这种离散数据生成问题直接使用 GAN 存在很多问题,特别是生成的数据缺乏局部一致性。
相比之下,SeqGAN 把生成器的输出作为一个智能体(agent)的策略,而判别器的输出作为奖励(reward),使用策略梯度下降来训练模型。ORGAN 则在 SeqGAN 的基础上,针对具体的目标设定了一个特定目标函数。
语言和语音
VAW-GAN (Variational autoencoding Wasserstein GAN) 结合 VAE 和 WGAN 实现了一个语音转换系统。编码器编码语音信号的内容,解码器则用于重建音色。由于 VAE 容易导致生成结果过于平滑,所以此处使用 WGAN 来生成更加清晰的语音信号。
半监督学习
图像数据的标签获得需要大量的人工标注,这个过程费时费力。
利用判别器进行半监督学习
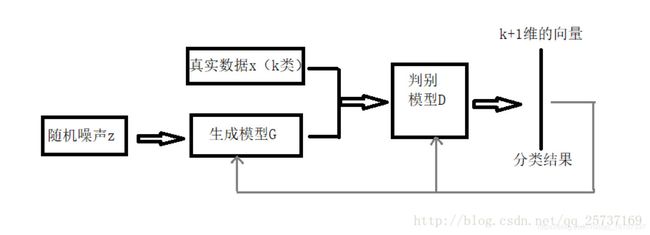
基于 GAN 的半监督学习方法 2 提出了一种利用无标签数据的方法。实现方法和原始 GAN 基本一样,具体框架如下:
相比于原始 GAN,主要区别在于判别器输出一个 K+1 的类别信息(生成的样本为第 K+1 类)。对于判别器,其 Loss 包括两部分,一个是监督学习损失(只需要判断样本真假),另一个是无监督学习损失(判断样本类别)。生成器则只需要尽量生成逼真的样本即可。训练完成后,判别器就可以作为一个分类模型去分类。
从直观上来看,生成的样本主要在于辅助分类器学会区分真实的数据空间在哪里。
使用辅助分类器的半监督学习
上面提及的利用判别器进行半监督学习的模型存在一个问题。判别器既要学习区分正负样本,也要学习预测标签。二者目标不一致,容易导致二者都达不到最优。一个直观的想法就把预测标签和区分正负样本分开。Triple-GAN 就是这么做的:
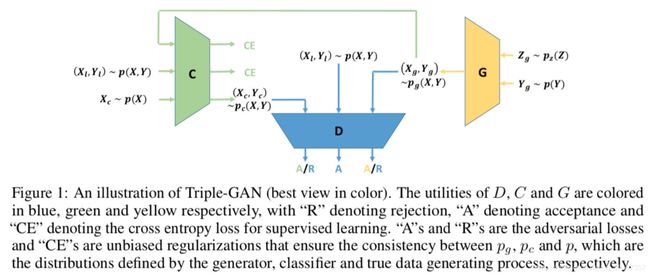
( X g , Y g ) ∼ p g ( X , Y ) , ( X l , Y l ) ∼ p ( X , Y ) , ( X c , Y c ) ∼ p c ( X , Y ) (X_g,Y_g) \sim p_g(X,Y), (X_l,Y_l) \sim p(X,Y),(X_c,Y_c) \sim p_c(X,Y) (Xg,Yg)∼pg(X,Y),(Xl,Yl)∼p(X,Y),(Xc,Yc)∼pc(X,Y) 分别表示生成的数据,有标签的数据,无标签的数据。CE 表示交叉熵损失。
域适应
域适应是一个迁移学习里面的概念。简单说来,我们定义源数据域分布为 D s ( x , y ) \mathbf D_s(x,y) Ds(x,y),目标数据域分布为 D T ( x , y ) \mathbf D_T(x,y) DT(x,y)。对于源域数据,我们有许多标签,但是对于目标域的数据没有标签。我们希望能通过源域的有标签数据和目标域的无标签数据学习一个模型,在目标域泛化的很好。迁移学习的“迁移”二字指的是源域数据分布向目标域数据分布的迁移。
GAN 用于迁移学习时,核心思想在于使用生成器把源域数据特征转换成目标域数据特征,而判别器则尽可能区分真实数据和生成数据特征。以下是两个把 GAN 应用于迁移学习的例子 DANN 和 ARDA:
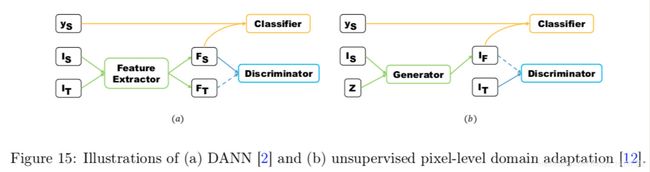
以上图左边的 DANN 为例, I s I_s Is, I t I_t It 分别代表源域数据,目标域的数据, y s y_s ys 表示源域数据的标签。 F s F_s Fs, F t F_t Ft 表示源域特征,目标域特征。DANN 中,生成器用于提取特征,并使得提取的特征难以被判别器区分是源域数据特征还是目标域数据特征。
在行人重识别领域,有许多基于 CycleGAN 的迁移学习以进行数据增广的应用。行人重识别问题一个难点在于不同摄像头下拍摄的人物环境,角度差别非常大,导致存在较大的 Domain gap。
因此,可以考虑使用 GAN 来产生不同摄像头下的数据进行数据增广。Zheng Z等人3 中提出了一个 CycleGAN 用于数据增广的方法。具体模型结构如下:
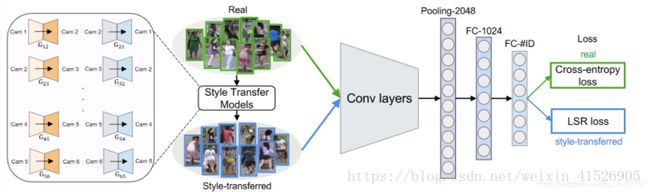
对于每一对摄像头都训练一个 CycleGAN,这样就可以实现将一个摄像头下的数据转换成另一个摄像头下的数据,但是内容(人物)保持不变。
其他应用
GAN 的变体繁多,应用非常广泛,在一写非机器学习领域也有应用,以下是一些例子。
医学图像分割
Yuan Xue 等人4 提出了一种 segmentor-critic 结构用于分割医学图像。segmentor 类似于 GAN 中的生成器用于生成分割图像,critic 则最大化生成的分割图像和 ground truth 之间的距离。此外,DI2IN 使用 GAN 分割 3D CT 图像,SCAN 使用 GAN 用于分割 X 射线图像。
图片隐写
隐写指的是把秘密信息隐藏到非秘容器,比如图片中。隐写分析器则用于判别容器是否含有秘密信息。一些研究尝试使用 GAN 的生成器生成带有隐写信息的图片,判别器则有两个,一个用于判别图片是否是真实图片,另一个则判别图片是否具有秘密信息 5。
连续学习
连续学习目的在于解决多个任务,且在学习过程中不断积累新知识。连续学习中存在一个突出的问题就是“知识遗忘”。6 中使用 GAN 的生成器作为一个 scholars model,生成器不断使用以往知识进行训练,solver 则给出答案,以此避免“知识遗忘”问题。
讨论
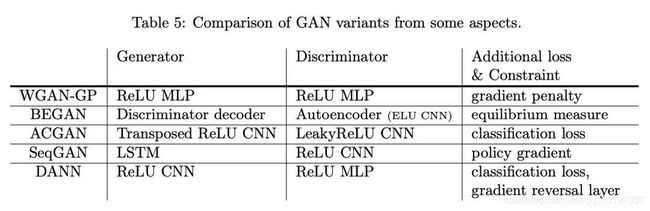
在第一、二部分我们讨论了 GAN 及其变体,第三部分讨论了 GAN 的应用。下表总结了比较有名的一些 GAN 的模型结构及其施加的额外约束。
前面都是对于 GAN 的微观层面的探讨。接下来,我们会站在一个宏观的视角来讨论 GAN。
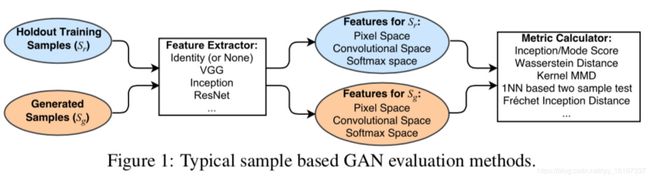
GAN的评价
GAN 的评价方法多种多样,现有的 example-based(顾名思义,基于样本层面做评价)方法,均是对生成样本与真实样本提取特征,然后在特征空间做距离度量。具体框架如下:
关于本小节的符号对照关系如下:
P g P_g Pg 表示生成数据分布, P r P_r Pr 表示真实数据分布, E E E 表示数学期望, x x x 表示输入样本, x ∼ P g x \sim P_g x∼Pg 表示 x x x 为生成样本的采样, x ∼ P r x \sim P_r x∼Pr 表示 x x x 为真实样本的采样。 y y y 表示样本标签, M M M 表示分类网络,通常选择 Inception network。
下面分别对常见的评价指标进行一一介绍。
Inception Score
对于一个在 ImageNet 训练良好的 GAN,其生成的样本丢给 Inception 网络进行测试的时候,得到的判别概率应该具有如下特性:
- 对于同一个类别的图片,其输出的概率分布应该趋向于一个脉冲分布。可以保证生成样本的准确性。
- 对于所有类别,其输出的概率分布应该趋向于一个均匀分布,这样才不会出现 mode collapsing 等,可以保证生成样本的多样性。
因此,可以设计如下指标:
I S ( P g ) = e E x ∼ P g [ K L ( p M ( y ∣ x ) ∥ p M ( y ) ) ] IS(P_g) = e^{E_{x \sim P_g}[KL(p_M(y|x) \| p_M(y))]} IS(Pg)=eEx∼Pg[KL(pM(y∣x)∥pM(y))]
根据前面分析,如果是一个训练良好的 GAN, p M ( y ∣ x ) p_M(y|x) pM(y∣x) 趋近于脉冲分布, p M ( y ) p_M(y) pM(y) 趋近于均匀分布。二者 K L KL KL散度会很大。Inception Score 自然就高。实际实验表明,Inception Score 和人的主观判别趋向一致。 I S IS IS 的计算没有用到真实数据,具体值取决于模型 M M M 的选择。
特点:可以一定程度上衡量生成样本的多样性和准确性,但是无法检测过拟合。Mode Score 也是如此。不推荐在和 ImageNet 数据集差别比较大的数据上使用。
Mode Score
Mode Score 作为 Inception Score 的改进版本,添加了关于生成样本和真实样本预测的概率分布相似性度量一项。具体公式如下:
M S ( P g ) = e E x ∼ P g [ K L ( p M ( y ∣ x ) ∥ p M ( y ) ) − K L ( p M ( y ) ∥ p M ( y ∗ ) ) ] MS(P_g) = e^{E_{x \sim P_g}[KL(p_M(y|x) \| p_M(y))-KL(p_M(y) \| p_M(y^*))]} MS(Pg)=eEx∼Pg[KL(pM(y∣x)∥pM(y))−KL(pM(y)∥pM(y∗))]
Kernel MMD(Maximum Mean Discrepancy)
计算公式如下:
M M D 2 ( P r , P g ) = E x r ∼ P r , x g ∼ P g [ ∥ ∑ i = 1 n 1 k ( x r ) − ∑ i = 1 n 2 k ( x g ) ∥ ] MMD^2(P_r,P_g) = E_{x_r \sim P_r , x_g \sim P_g}[\| \sum_{i=1}^{n1} k(x_r)-\sum_{i=1}^{n2} k(x_g)\|] MMD2(Pr,Pg)=Exr∼Pr,xg∼Pg[∥i=1∑n1k(xr)−i=1∑n2k(xg)∥]
对于 Kernel MMD 值的计算,首先需要选择一个核函数 k,这个核函数把样本映射到再生希尔伯特空间**(Reproducing Kernel Hilbert Space, RKHS)**,RKHS 相比于欧几里得空间有许多优点,对于函数内积的计算是完备的。将上述公式展开即可得到下面的计算公式:
M M D 2 ( P r , P g ) = E x r , x r ′ ∼ P r , x g , x g ′ ∼ P g [ k ( x r , x r ′ ) − 2 k ( x r , x g ) + k ( x g , x g ′ ) ] MMD^2(P_r,P_g) = E_{x_r,{x_r}' \sim P_r ,x_g, {x_g}' \sim P_g}[k(x_r,{x_r}')-2k(x_r,x_g)+k(x_g,{x_g}')] MMD2(Pr,Pg)=Exr,xr′∼Pr,xg,xg′∼Pg[k(xr,xr′)−2k(xr,xg)+k(xg,xg′)]
MMD 值越小,两个分布越接近。
特点:可以一定程度上衡量模型生成图像的优劣性,计算代价小。推荐使用。
Wasserstein Distance
Wasserstein distance 在最优传输问题中通常也叫做推土机距离。这个距离的介绍在 WGAN 中有详细讨论。公式如下:
W D ( P r , P g ) = min w ∈ R m × n ∑ i = 1 n ∑ i = 1 m ω i j d ( x i r , x j g ) s . t . ∑ i = 1 m ω i , j = p r ( x i r ) , ∀ i ; ∑ j = 1 m ω i , j = p g ( x j g ) , ∀ j ; WD(P_r,P_g) = \min _{w \in \mathbf R^{m \times n}} \sum_{i=1}^n \sum_{i=1}^m \omega_{ij} d(x_i^r,x_j^g) \\ s.t. \sum_{i=1}^m \omega_{i,j} = p_r(x_i^r) , \forall i; \\ \sum_{j=1}^m \omega_{i,j} = p_g(x_j^g) , \forall j; WD(Pr,Pg)=w∈Rm×nmini=1∑ni=1∑mωijd(xir,xjg)s.t.i=1∑mωi,j=pr(xir),∀i;j=1∑mωi,j=pg(xjg),∀j;
Wasserstein distance 可以衡量两个分布之间的相似性。距离越小,分布越相似。
特点:如果特征空间选择合适,会有一定的效果。但是计算复杂度为 O(n^3) 太高。
Fréchet Inception Distance (FID)
FID 距离计算真实样本,生成样本在特征空间之间的距离。首先利用 Inception 网络来提取特征,然后使用高斯模型对特征空间进行建模。根据高斯模型的均值和协方差来进行距离计算。具体公式如下:
F I D ( P r , P g ) = ∥ μ r − μ g ∥ + T r ( C r + C g − 2 ( C r , C g ) 1 / 2 ) FID(\mathbf P_r, \mathbf P_g) = \| \mu_r -\mu_g \| + T_r(C_r+C_g-2(C_r,C_g)^{1/2}) FID(Pr,Pg)=∥μr−μg∥+Tr(Cr+Cg−2(Cr,Cg)1/2) μ , C \mu ,C μ,C 分别代表协方差和均值。
特点:尽管只计算了特征空间的前两阶矩,但是鲁棒,且计算高效。
1-Nearest Neighbor classifier
使用留一法,结合 1-NN 分类器(别的也行)计算真实图片,生成图像的精度。如果二者接近,则精度接近 50%,否则接近 0%。对于 GAN 的评价问题,作者分别用正样本的分类精度,生成样本的分类精度去衡量生成样本的真实性,多样性。
- 对于真实样本 X r X_r Xr ,进行 1-NN 分类的时候,如果生成的样本越真实。则真实样本空间 R R R 将被生成的样本 X g X_g Xg 包围。那么 X r X_r Xr 的精度会很低。
- 对于生成的样本 X g X_g Xg ,进行 1-NN 分类的时候,如果生成的样本多样性不足。由于生成的样本聚在几个 mode,则 X g X_g Xg 很容易就和 X r X_r Xr 区分,导致精度会很高。
特点:理想的度量指标,且可以检测过拟合。
其他评价方法
AIS,KDE 方法也可以用于评价 GAN,但这些方法不是 model agnostic metrics。也就是说,这些评价指标的计算无法只利用:生成的样本,真实样本来计算。
总结
实际实验发现,MMD 和 1-NN two-sample test 是最为合适的评价指标,这两个指标可以较好的区分:真实样本和生成的样本, mode collapsing。且计算高效。
总体说来,GAN 的学习是一个无监督学习过程,所以很难找到一个比较客观的,可量化的评估指标。有许多指标在数值上虽然高,但是生成效果却未必好。总之,GAN 的评价目前依然是一个开放性的问题。
GAN与强化学习的关系
强化学习的目标是对于一个智能体,给定状态 s s s,去选择一个最佳的行为 a a a (action)。通常的可以定义一个价值函数 Q ( s , a ) Q(s,a) Q(s,a) 来衡量,对于状态 s s s,采取行动 a a a 的回报是 Q ( s , a ) Q(s,a) Q(s,a),显然,我们希望最大化这个回报值。对于很多复杂的问题,我们是很难定义这个价值函数 Q ( s , a ) Q(s,a) Q(s,a) 的,就像我们很难定义 GAN 生成的图片到底有多好一样。
说到这里,大家可能反应过来了。GAN 生成的图片好不好,我确实找不到一个合适的指标,那我学习一个判别器去判断一下生成图片和真实图片的距离不就好了吗。强化学习里面的价值函数 Q ( s , a ) Q(s,a) Q(s,a) 难以定义,那直接用个神经网络去学习它就好了。典型的模型有 DDPG,TRPO 等等。
GAN的优缺点
优点
GAN 的优点在开头已有所介绍。这里再总结一下:
- GAN 可以并行生成数据。相比于 PixelCNN,PixelRNN 这些模型,GAN 生成非常快,因为 GAN 使用 Generator 替代了采样的过程;
- GAN 不需要通过引入下界来近似似然。VAE 由于优化困难,引入了变分下界来优化似然。但是 VAE 对于先验和后验分布做了假设,使得 VAE 很难逼近其变分下界;
- 从实践来看,GAN 生成的结过要比 VAE 更清晰的多。
缺点
GAN 的缺点在前文也有详细讨论,主要问题在于:
- 训练不稳定,容易崩溃。这个问题有学者提出了许多解决方案,比如 WGAN,LSGAN 等;
- 模式崩溃。尽管有很多相关的研究,但是由于图像数据的高维度特性,这个问题依然还没完全解决。
未来的研究方向
- GAN 的训练崩溃,模式崩溃问题等依然有待研究改进。
- Deep learning 尽管很强大,但目前仍有许多领域无法征服,期待 GAN 在此基础上会有一些作为。
Hong Y, Hwang U, Yoo J, et al. How Generative Adversarial Networks and its variants Work: An Overview of GAN[J]. ArXiv171105914 Cs, 2017. ↩︎
Salimans, Tim, et al. “Improved techniques for training gans.” Advances in neural information processing systems. 2016. ↩︎
Zheng Z , Zheng L , Yang Y . Unlabeled Samples Generated by GAN Improve the Person Re-identification Baseline in VitroC// 2017 IEEE International Conference on Computer Vision (ICCV). IEEE Computer Society, 2017. ↩︎
Yuan Xue, Tao Xu, Han Zhang, Rodney Long, and Xiaolei Huang. Segan: Adversar- ial network with multi-scale l_1 loss for medical image segmentation. arXiv preprint arXiv:1706.01805, 2017. ↩︎
Denis Volkhonskiy, Ivan Nazarov, Boris Borisenko, and Evgeny Burnaev. Steganographicgenerative adversarial networks. arXiv preprint arXiv:1703.05502, 2017. ↩︎
Shin, Hanul, et al. “Continual learning with deep generative replay.” Advances in Neural Information Processing Systems. 2017. ↩︎