目录
- 一、为什么要学习算法与数据结构
- 二、算法概述
- 三、常见排序算法
- 3.1 直接插入排序(insert sort)
- 3.2 希尔排序(shell sort)
- 3.3 简单选择排序(select sort)
- 3.4 冒泡排序(bubble sort)
- 3.5 快速排序
- 3.6 归并排序(merge sort)
- 3.7 排序总结
- 四、计数排序(count sort)
- 五、桶排序(bucket sort)
- 六、基数排序
一、为什么要学习算法与数据结构
- 算法说直白点算是检验一个人的脑回路了,一个人脑子调理请不清晰,看算法学的好不好,就可以看出个90%
- 个人觉得算法十比较有趣的,并且很多人都在学
二、算法概述
定义:一个计算过程,解决问题的方法,而程序=数据结构+算法。
时间复杂度:⽤来评估算法运⾏效率的⼀个式⼦。
print('hello Cecilia') # 时间复杂度为O(1) for i in range(n): print('hello Cecilia') # 时间复杂度为O(n) for i in range(n): print('hello Cecilia') for i in range(n): print('hello Cecilia') # 时间复杂度为O(n^2) for i in range(n): print('hello Cecilia') for i in range(n): print('hello Cecilia') for i in range(n): print('hello Cecilia') # 时间复杂度为O(n^3)def func(n): while n > 1: print(n) n = n // 2 func(64) #当算法过程出现循环折半时,时间复杂度记为O(logn) # 64 # 32 # 16 # 8 # 4 # 2- 如何简单快速的判断时间复杂度(适用于大多数情况)?
- 确定问题规模n
- 循环减半过程——logn
- k层关于n的循环——n^k
- 空间复杂度:⽤来评估算法内存占⽤⼤⼩的式⼦。空间换时间,表达式跟时间复杂度一样,如下:
- 算法使⽤了⼏个变量:O(1)
- 算法使⽤了⻓度为n的⼀维列表:O(n)
- 算法使⽤了m⾏n列的⼆维列表:O(mn)
三、常见排序算法
3.1 直接插入排序(insert sort)
定义:我们这里以打不可派举例把、当我们在打牌之前每个人都要取摸牌,二没摸一次牌,我们则对拿当前摸得牌和手里已经有的拍进行依次对比,然后找到它对应的位置以后,把他直接放进去,这里需要注意的是,我们的牌默认是从小到大排序的,所以就有了我们直接插入排序的概念:假使一个列表,列表本来就一个元素,则后面再往列表中添加元素的时候,新添加的元素一定要和前面的比较,那这里我们直接插入排序待排序的列表有n个元素,那我们就拿列表的每一个元素和前面的一个元素进行比较,并且再比较的时候,我们的当前元素之前的每个元素默认是拍好顺序的,所以只有当前的元素比它前一个元素小的时候,让这两个元素交换位置,并且继续往前比较,不大于则进行下一个元素的比较
# 这里实现是用python来实现的
def insert_sort(List):
第一层循环,遍历第二个元素后面的每一个元素
for x in range(1,len(L)):
第二层循环,选择的每一个元素和他前面的每一个元素比较大小
for i in range(x-1,-1,-1):
if L[i] > L[i+1]:
temp = L[i+1] # 这里使用的是中间变量来进行两个值的交换
L[i+1] = L[i]
L[i] = temp
return List
l=[9,2,45,6,4,23,7,8,6,74,3,35,456,44]
res = insert_sort(l)
print(res)
#时间复杂度为o(n^2)3.2 希尔排序(shell sort)
定义:分组插⼊排序算法。
思想:
- ⾸先取⼀个整数gap=(待排序列表的长度)/2,将元素分为gap个组,每组相邻两元素之间距离为gap,在各组内进⾏直接插⼊排序;
- 取第⼆个整数gap=gap/2,重复上述分组排序过程,直到gap=1,即所有元素在同⼀组内进⾏直接插⼊排序。
- 希尔排序每趟并不使某些元素有序,⽽是使整体数据越来越接近有序;最后⼀趟排序使得所有数据有序。
def shel_insert(L):
gap = (int)(len(L)/2) # 首先得到这个定值gap
while (gap >= 1): # gap必须是要>=1
# 从gap值开始,循环列表的gap位置后的元素
for x in range(gap,len(L)):
# 从列表的gap位置-gap值开始取值
# 每次取的到-1前的0位置结束,步长为-gap就实现倒着取
for i in range(x-gap,-1,-gap):
# 判断当前取到的值和它组内的一个元素比较大小,然后再判断是否交换位置
if L[i] > L[i+gap]:
temp = L[i+gap]
L[i+gap] = L[i]
L[i] =temp
print(L)
gap = (int)(gap/2)# 每次最外层循环结束以后,gap的值//2
shel_insert([9,2,45,6,4,23,7,8,6,74,3,35,456,44])
# 希尔排序的时间复杂度讨论⽐较复杂,并且和选取的gap序列以及列表的长度有关。3.3 简单选择排序(select sort)
基本思想:比较+交换
解决流程:
- 从待排序序列中,取第一个元素作为序列的最小元素,就是序列开始比较的当前位置
- 拿这个最小元素和序列当前位置后面所有元素依次进行比较,如果遇到比当前最小元素小的,则更改最小元素的值
- 直到与序列后的每一个元素比较完以后,确定找到一个最小的值,然后放在序列的当前位置
总结:简单选择排序也是通过两层循环
第一层:依次遍历依次遍历序列当中的每一个元素
第二层循环:将遍历得到的当前元素依次与余下的元素进行比较,符合最小元素的条件,则交换。
l = [9,2,45,6,4,23,7,8,6,74,3,35,456,44]
print(l)
# 依次遍历列表中的每一个元素
for i in range(len(l)):
# 以当前的位置的元素作为最小的一个元素
res = l[i]
# 循环当前作为最小元素后的每一个元素,然后与之做比较
for j in range(i+1,len(l)):
# 若当前元素小于我最开始设置的最小元素,那么就将最开始设置的最小元素和当前与它比较的元素交换
if l[j] < res:
temp = l[j]
l[j] = res
res = temp
print(l)
# 直到最小元素与后面的每一个元素比较结束以后,将这个最小值放在排序列表的当前位置[0,1,2,3,4,......]
l[i]=res
print(l)3.4 冒泡排序(bubble sort)
冒泡排序的思想
- 保证排序序列中所有的左右元素,有右边的元素总是大于左边的元素的
- 在第一次循环结束以后,排好的序列中,最后一个一定是所有元素最大的一个元素
- 对于剩下的n-1次循环,一样是重复之前的操作
总结: 冒泡排序就是将序列中的每一个元素和后面的一个元素进行排序,左右一定是右边的比左边的大
- 一样需要两层循环
- 第一层:循环序列长度-1次
- 第二层:从序列的第一个元素开始每一次从当前元素和序列长度的-当前循环的几次的之前的每一个元素进行比较
l = [9,2,45,6,4,23,7,8,6,74,3,35,456,44]
lens = len(l)
for i in range(1,lens):
for j in range(0,lens-i): # 每一次排序都找到一个最大值,在序列的最后一个位置上
if l[j] > l[j+1]:
l[j],l[j+1]= l[j+1],l[j]
print(l)
print(l)3.5 快速排序
快速排序的思想:
- 取⼀个元素p(第⼀个元素),使元素p归位;
- 列表被p分成两部分,左边都⽐p⼩,右边都⽐p⼤;
- 递归完成排序。
快速排序的时间复杂度:O(nlogn),完全倒序时间复杂度时:O(n^2)
特殊情况:达到最大递归深度,但是可以修改。
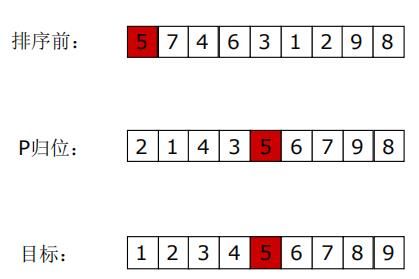
p如何实现归位,以上图为例:先将5拿出来,左指针left和右指针right分别放于两端,假设按顺序升序排序,当右指针移到2时比5小移到5原来的位置,再从左边开始,发现7比5大,将7移到原来2的位置,再从右边开始发现1比5小,将1移动到原来7的位置,再从左边开始移动,4比5小不移动,发现6比5大,所以将6移动到原来1的位置,再从右边开始,发现3比5小,将3移动到原来6的位置,此时3和6之间存在一个空位置,就将5放到该位置,实现了p归位。
def quick_sort(List, left, right): #列表、左指针位置、右指针位置
if left < right:
mid = partition(List, left, right) # 归位位置
quick_sort(List, left, mid - 1) # 递归原函数
quick_sort(List, mid + 1, right)
def partition(li, left, right):
"""求归位元素函数"""
tmp = li[left] # 初始值:归位元素
while left < right:
while left < right and li[right] >= tmp: right -= 1 # 从右面找比tmp小的元素,若右面元素大于等于tmp往左移动一位且如果碰上跳出本次循环
li[left] = li[right] # 把右边的值赋值给左边空位上
while left < right and li[left] <= tmp: left += 1 # 从左面找比tmp大的元素,若左面元素小于等于tmp往右移动一位且如果碰上跳出本次循环
li[right] = li[left] # 把左边的值赋值给右边空位上
li[left] = tmp
return left
def quick_sort(li, left, right):
"""快速排序函数"""
if left < right:
mid = partition(li, left, right)
quick_sort(li, left, mid - 1)
quick_sort(li, mid + 1, right)
li = [5, 7, 4, 6, 3, 1, 2, 9, 8]
quick_sort(li, 0, len(li) - 1)
print(li)
# 装饰器不能直接加在递归函数上,不然装饰器跟着递归:
import time
import random
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
res = func(*args, **kwargs)
t2 = time.time()
print(f'{func.__name__} running time:{t2 - t1} secs')
return res
return wrapper
def partition(li, left, right):
"""求归位元素函数"""
tmp = li[left] # 初始值:归位元素
while left < right:
# 从右面找比tmp小的元素,若右面元素大于等于tmp往左移动一位且如果碰上跳出本次循环
while left < right and li[right] >= tmp: right -= 1
li[left] = li[right] # 把右边的值赋值给左边空位上
# 从左面找比tmp大的元素,若左面元素小于等于tmp往右移动一位且如果碰上跳出本次循环
while left < right and li[left] <= tmp: left += 1
li[right] = li[left] # 把左边的值赋值给右边空位上
li[left] = tmp
return left
def _quick_sort(li, left, right): # 换马甲
if left < right:
mid = partition(li, left, right)
_quick_sort(li, left, mid - 1)
_quick_sort(li, mid + 1, right)
@cal_time
def quick_sort(li, left, right):
_quick_sort(li, left, right)
li = list(range(10000))
random.shuffle(li)
quick_sort(li, 0, len(li) - 1)3.6 归并排序(merge sort)
一次归并操作:假设现在的列表分两段有序,如何将其合成为⼀个有序列表,如[2,5,7,8,9,1,3,4,6]
归并解题思路:
- 分解:将列表越分越⼩,直⾄分成⼀个元素。
- 终⽌条件:⼀个元素是有序的。
- 合并:将两个有序列表归并,列表越来越⼤。
import random
def merge(li, low, mid, high):
"""
一次归并函数
li: 列表
low: 开始位置索引
mid: 中间位置索引
high: 末位置索引
return:
"""
i = low
j = mid + 1
tmp = []
while i <= mid and j <= high: # 保证两边都有值,循环完肯定有一边没数了。
if li[i] < li[j]:
tmp.append(li[i])
i += 1
else:
tmp.append(li[j])
j += 1
while i <= mid: # 假设左边有数,循环左边
tmp.append(li[i])
i += 1
while j <= high: # 假设右边有数,循环右边
tmp.append(li[j])
j += 1
li[low:high + 1] = tmp # 重新赋值
def merge_sort(li, low, high):
"""归并排序"""
if low < high: # 保证至少有两个元素才能递归
mid = (low + high) // 2
merge_sort(li, low, mid)
merge_sort(li, mid + 1, high)
merge(li, low, mid, high)
li = list(range(20))
random.shuffle(li)
merge_sort(li, 0, len(li) - 1)
print(li)
# 时间复杂度:O(nlogn);空间复杂度:O(n)3.7 排序总结
快速排序、堆排序、归并排序算法的时间复杂度都是O(nlogn)
⼀般情况下,就运⾏时间⽽⾔: 快速排序 < 归并排序 < 堆排序
三种排序算法的缺点:
快速排序:极端情况下排序效率低
归并排序:需要额外的内存开销
堆排序:在快的排序算法中相对较慢四、计数排序(count sort)
定义:对列表进⾏排序,已知列表中的数范围都在0到100之间。设计时间复杂度为O(n)的算法。
def count_sort(li, max_count=100):
count = [0 for _ in range(max_count + 1)]
for val in li:
count[val] += 1
li.clear()
for ind, val in enumerate(count):
for i in range(val):
li.append(ind)
import random
li = [random.randint(0, 100) for _ in range(1000)]
count_sort(li)
print(li)五、桶排序(bucket sort)
定义:⾸先将元素分在不同的桶中,在对每个桶中的元素排序。在计数排序中,如果元素的范围⽐较⼤(⽐如在1到1亿之间), 如何改造算法?
def bucket_sort(li, n=100, max_num=10000):
buckets = [[] for _ in range(n)] # 创建桶
for var in li:
i = min(var // (max_num // n), n - 1) # i表示var放到几号桶里
buckets[i].append(var)
for j in range(len(buckets[i]) - 1, 0, -1):
if buckets[i][j] < buckets[i][j - 1]:
buckets[i][j], buckets[i][j - 1] = buckets[i][j - 1], buckets[i][j]
else:
break
sorted_li = []
for buc in buckets:
sorted_li.extend(buc)
return sorted_li
import random
li = [random.randint(0, 10000) for i in range(100000)]
li = bucket_sort(li)
print(li)
#桶排序的表现取决于数据的分布。也就是需要对不同数据排序时采取不同的分桶策略。
#平均情况时间复杂度:O(n+k)
#最坏情况时间复杂度:O(n2k)
#空间复杂度:O(nk)六、基数排序
多关键字排序:加⼊现在有⼀个员 ⼯表,要求按照薪资排序,年龄相同的员⼯按照年龄排序。 先按照年龄进⾏排序,再按照薪资进⾏稳定的排序。 对32,13,94,52,17,54,93排序,是否可以看做多关键字排序?
def list_to_buckets(li, base, iteration):
buckets = [[] for _ in range(base)]
for number in li:
digit = (number // (base ** iteration)) % base
buckets[digit].append(number)
return buckets
def buckets_to_list(buckets):
return [x for bucket in buckets for x in bucket]
def radix_sort(li, base=10):
maxval = max(li)
it = 0
while base ** it <= maxval:
li = buckets_to_list(list_to_buckets(li, base, it))
it += 1
return li
# 时间复杂度:O(kn)
# 空间复杂度:O(k+n)
# k表示数字位数