数学基础(二):凸优化基础(仿射集,凸集,凸优化问题)
凸优化基础
数学基础系列博客是自己在学习了稀牛学院&网易云课堂联合举办的《人工智能数学基础》微专业后的课程笔记总结。怀着对授课讲师Jason博士无限的敬佩与感激之情,我在完整听了两遍课程之后,对这门进行了笔记整理。Jason博士用深入浅出的方式把数学知识真的是讲透彻了,我的笔记显然无法完整传达Jason博士的精彩授课内容,在此非常推荐每一个打算进入或了解AI的同学去学习这门课程!
一:一般优化问题
1.1 无约束优化问题
自变量为矢量的函数 f : R n → R f: \mathbf{R}^n\rightarrow \mathbf{R} f:Rn→R:
m i n f ( x ) x ∈ R n minf(\mathbf{x})\quad \mathbf{x} \in \mathbf{R}^n minf(x)x∈Rn
求解方法有两种:(均求得局部最优解,不一定是全局最优解,因为不知道函数的形状)
- 直接法求解。令 ∇ f ( x ) = 0 \nabla f(\mathbf{x})=0 ∇f(x)=0,求得驻点,如果有必要,则再根据Hessian矩阵的正定性判断驻点的性质(局部极大、局部极小、鞍点)
- 迭代法求解
- 梯度下降法( d k = − g k ) d_k=-g_k) dk=−gk),每次下降的方向为负梯度方向。
- 牛顿法( d k = − H k − 1 g k d_k=-H_k^{-1}g_k dk=−Hk−1gk),考虑泰勒级数中的二阶项。
- 拟牛顿法(避免求Hessian矩阵的逆,使用另一个矩阵 S k S_k Sk近似)
- DFP
- BFGS
- 两者的区别在于 S k S_k Sk的不同。
1.2 有约束优化问题
- 约束优化问题的一般形式:
m i n m i z e f 0 ( x ) s u b j e c t t o f i ( x ) ≤ 0 f o r i = 1 , 2 , . . . m h i ( x ) = 0 f o r i = 1 , 2 , . . . p minmize\quad f_0(\mathbf{x})\\ subject\ to\ f_i(\mathbf{x})\le0 \quad for\ i = 1,2,...m\\ \quad \quad \quad \quad h_i(\mathbf{x}) = 0\quad for\ i=1,2,...p minmizef0(x)subject to fi(x)≤0for i=1,2,...mhi(x)=0for i=1,2,...p
-
可行域:满足 f ( x ) f(\mathbf{x}) f(x)定义域和约束条件的 x \mathbf{x} x的集合。
-
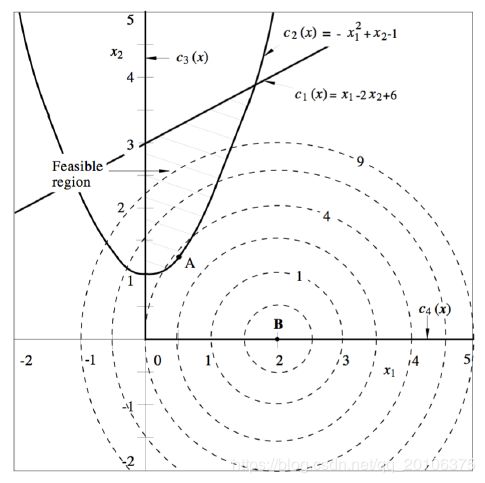
举例:下图中虚线为等高线
minimize f ( x ) = x 1 2 + x 2 2 − 4 x 1 + 4 = ( x 1 − 2 ) 2 + x 2 2 subject to c 1 ( x ) = x 1 − 2 x 2 + 6 ≥ 0 c 2 ( x ) = − x 1 2 + x 2 − 1 ≥ 0 , c 3 ( x ) = x 1 ≥ 0 , c 4 ( x ) = x 2 ≥ 0 \text{minimize} \quad f(\mathrm{x})=x_{1}^{2}+x_{2}^{2}-4 x_{1}+4=\left(x_{1}-2\right)^{2}+x_{2}^{2}\\ \text{subject to} \quad c_{1}(\mathrm{x})=x_{1}-2 x_{2}+6 \geq 0\\ \qquad \qquad \qquad c_{2}(\mathrm{x})=-x_{1}^{2}+x_{2}-1 \geq 0, \\\quad c_{3}(\mathrm{x})=x_{1} \geq 0, \\\quad c_{4}(\mathrm{x})=x_{2} \geq 0 minimizef(x)=x12+x22−4x1+4=(x1−2)2+x22subject toc1(x)=x1−2x2+6≥0c2(x)=−x12+x2−1≥0,c3(x)=x1≥0,c4(x)=x2≥0
1.3 补充知识 A x = b \mathbf{Ax=b} Ax=b
矩阵乘法
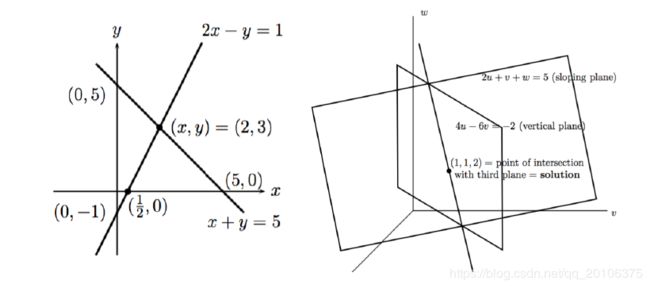
[ 2 − 1 1 1 ] ⎵ A ∈ R 2 × 2 [ x y ] ⎵ x ∈ R 2 = [ 1 5 ] ⎵ b ∈ R 2 \underbrace{\left[ \begin{array}{cc}{2} & {-1} \\ {1} & {1}\end{array}\right]}_{\mathbf{A} \in \mathbb{R}^{2 \times 2}} \underbrace{\left[ \begin{array}{l}{x} \\ {y}\end{array}\right]}_{\mathbf{x} \in \mathbb{R}^{2}}=\underbrace{\left[ \begin{array}{l}{1} \\ {5}\end{array}\right]}_{\mathbf{b} \in \mathbb{R}^{2}} A∈R2×2 [21−11]x∈R2 [xy]=b∈R2 [15]
[ 2 1 1 4 − 6 0 − 2 7 2 ] ⎵ A ∈ R 3 × 3 [ u v w ] ⎵ x ∈ R 3 = [ 5 − 2 9 ] ⎵ b ∈ R 3 \underbrace{\left[ \begin{array}{ccc}{2} & {1} & {1} \\ {4} & {-6} & {0} \\ {-2} & {7} & {2}\end{array}\right]}_{\mathbf{A} \in \mathbb{R}^{3 \times 3}} \underbrace{\left[ \begin{array}{l}{u} \\ {v} \\ {w}\end{array}\right]}_{\mathbf{x} \in \mathbb{R}^{3}}=\underbrace{\left[ \begin{array}{c}{5} \\ {-2} \\ {9}\end{array}\right]}_{\mathbf{b} \in \mathbb{R}^{3}} A∈R3×3 ⎣⎡24−21−67102⎦⎤x∈R3 ⎣⎡uvw⎦⎤=b∈R3 ⎣⎡5−29⎦⎤
对于 A x = b \mathbf{Ax=b} Ax=b,从行视图的角度,可以理解为多个超平面的交集。所谓超平面,在二维空间中指直线,在三维空间中指平面。在更高维空间中,不可以可视化,但可以类比理解为 y = w T x + b y = \mathbf{w^Tx}+b y=wTx+b的平面。
二:凸集和凸函数
2.1 凸集
2.1.1 凸集和仿射集
-
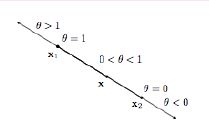
仿射集:集合中任意两点间的直线也在集合中,那么该集合称为仿射集。例如 x = θ x 1 + ( 1 − θ ) x 2 ∈ C , ( C ∈ R n , θ ∈ R ) \mathbf{x}=\theta\mathbf{x_1}+(1-\theta)\mathbf{x_2}\in C,\quad (C\in \mathbf{R}^n,\theta \in R) x=θx1+(1−θ)x2∈C,(C∈Rn,θ∈R).
-
A x = b \mathbf{Ax=b} Ax=b的解的集合为仿射集。 A x = A ( θ x 1 + ( 1 − θ ) x 2 ) = θ A x 1 + ( 1 − θ ) A x 2 = θ b + ( 1 − θ ) b = b \mathbf{Ax}=\mathbf{A}(\theta\mathbf{x_1}+(1-\theta)\mathbf{x_2})=\theta \mathbf{Ax_1}+(1-\theta) \mathbf{Ax_2}=\theta b+(1-\theta)b=b Ax=A(θx1+(1−θ)x2)=θAx1+(1−θ)Ax2=θb+(1−θ)b=b.
如果 x 1 \mathbf{x_1} x1和 x 2 \mathbf{x_2} x2都为方程组的解,那么 x 1 \mathbf{x_1} x1和 x 2 \mathbf{x_2} x2连接组成的直线是的任意一点 x \mathbf{x} x也是方程组的解。所以解的集合就是 x \mathbf{x} x,是一个仿射集。
-
凸集:集合中任意两点间的线段也在集合中,那么该集合称为凸集。例如:对于 x 1 , x 2 ∈ C \mathbf{x_1,x_2}\in C x1,x2∈C,有 x = θ x 1 + ( 1 − θ ) x 2 ∈ C , ( C ∈ R n , θ ∈ [ 0 , 1 ] ) \mathbf{x}=\theta\mathbf{x_1}+(1-\theta)\mathbf{x_2}\in C,\quad (C\in \mathbf{R}^n,\theta \in [0,1]) x=θx1+(1−θ)x2∈C,(C∈Rn,θ∈[0,1]).
-
一个集合是仿射集,但不一定是凸集;一个集合如果是凸集,那么一定是仿射集。
2.1.2 常见的凸集
part1
- 所有的 R n \mathbf{R}^n Rn,既是凸集又是仿射集。
- 所有的 R + n \mathbf{R}^n_+ R+n,只是凸集,因为是半空间。
- 超平面: C = { x ∣ a T x = b } C=\{\mathbf{x|a^Tx}=b\} C={x∣aTx=b},既是仿射集又是凸集。
- 半空间: C = { x ∣ a T x ≥ b } C=\{\mathbf{x|a^Tx}\ge b\} C={x∣aTx≥b}或者 C = { x ∣ a T x ≤ b } C=\{\mathbf{x|a^Tx}\le b\} C={x∣aTx≤b}。
part2
首先补充向量范数的知识:
-
2-norm:
∥ x ∥ 2 = ∑ i = 1 n ∣ x i ∣ 2 = ( x T x ) 1 / 2 \|\mathbf{x}\|_{2}=\sqrt{\sum_{i=1}^{n}\left|x_{i}\right|^{2}}=\left(\mathbf{x}^{T} \mathbf{x}\right)^{1 / 2} ∥x∥2=i=1∑n∣xi∣2=(xTx)1/2 -
1-norm:(绝对值相加)
∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ \|\mathbf{x}\|_{1}=\sum_{i=1}^{n}\left|x_{i}\right| ∥x∥1=i=1∑n∣xi∣ -
∞ \infty ∞-norm:(绝对值最大的那个数的值)
∥ x ∥ ∞ = max i = 1 , … , n ∣ x i ∣ \|\mathbf{x}\|_{\infty}=\max _{i=1, \ldots, n}\left|x_{i}\right| ∥x∥∞=i=1,…,nmax∣xi∣ -
p-norm( p ≥ 1 ) p \ge1) p≥1):
∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 p \|\mathbf{x}\|_{p}=\left(\sum_{i=1}^{n}\left|x_{i}\right|^{p}\right)^{\frac{1}{p}} ∥x∥p=(i=1∑n∣xi∣p)p1
注意p一定要大于等于1
-
范数球:例如 ∣ ∣ x ∣ ∣ 2 ≤ 1 ||\mathbf{x}||_2 \le1 ∣∣x∣∣2≤1.给定任意的 x , y ∈ R n \mathbf{x,y}\in \mathbf{R}^n x,y∈Rn,且 ∣ ∣ x ∣ ∣ 2 ≤ 1 , ∣ ∣ y ∣ ∣ 2 ≤ 1 ||\mathbf{x}||_2 \le1,||\mathbf{y}||_2 \le1 ∣∣x∣∣2≤1,∣∣y∣∣2≤1,则有 ∣ ∣ ∣ θ x + ( 1 − θ ) y ∣ ∣ 2 ≤ θ ∣ ∣ x ∣ ∣ 2 + ( 1 − θ ) ∣ ∣ y ∣ ∣ 2 ≤ 1 |||\theta\mathbf{x}+(1-\theta)\mathbf{y}||_2 \le \theta||\mathbf{x}||_2+(1-\theta)||\mathbf{y}||_2 \le1 ∣∣∣θx+(1−θ)y∣∣2≤θ∣∣x∣∣2+(1−θ)∣∣y∣∣2≤1.所以二范数围成的集合是凸集。
-
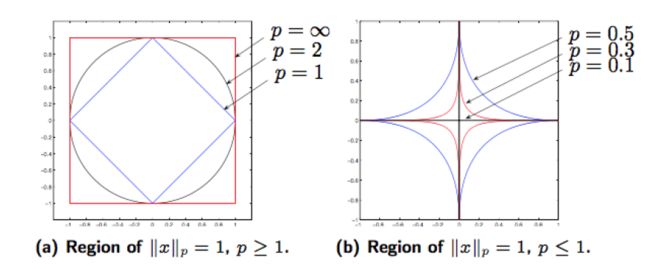
在二维情形下,
- ∣ ∣ x ∣ ∣ 1 ≤ 1 → ∣ x ∣ + ∣ y ∣ ≤ 1 ||\mathbf{x}||_1 \le1\rightarrow |x|+|y| \le 1 ∣∣x∣∣1≤1→∣x∣+∣y∣≤1;
- ∣ ∣ x ∣ ∣ 2 ≤ 1 → x 2 + y 2 ≤ 1 ||\mathbf{x}||_2 \le1\rightarrow x^2+y^2 \le1 ∣∣x∣∣2≤1→x2+y2≤1;
- ∣ ∣ x ∣ ∣ ∞ ≤ 1 → ∣ x ∣ ≤ 1 a n d ∣ y ∣ ≤ 1 ||\mathbf{x}||_{\infty} \le1\rightarrow |x|\le1 \ and \ |y| \le 1 ∣∣x∣∣∞≤1→∣x∣≤1 and ∣y∣≤1
-
当 p ≥ 1 p \ge1 p≥1时,范数球组成的集合是凸集。
part3
-
凸集的性质:凸集的交集是凸集,例如: S = { ∣ ∣ x ∣ ∣ 2 ≤ 1 , x ≥ 0 } S=\{||\mathbf{x}||_2 \le1,x \ge 0\} S={∣∣x∣∣2≤1,x≥0}, ∣ ∣ x ∣ ∣ 2 ≤ 1 ||\mathbf{x}||_2 \le1 ∣∣x∣∣2≤1是范数球,凸集; x ≥ 0 x \ge0 x≥0是半空间,凸集;凸集的交集还是凸集。所以 S S S是凸集。
证明:假定 S 1 , ⋯ , S k S_{1}, \cdots, S_{k} S1,⋯,Sk是凸集,给定 x , y ∈ ⋂ i = 1 k S i \mathbf{x}, \mathbf{y} \in \bigcap_{i=1}^{k} S_{i} x,y∈⋂i=1kSi(即x和y都是交集中的点),则有:
θ x + ( 1 − θ ) y ∈ S i , i = 1 , ⋯ , k \theta \mathrm{x}+(1-\theta) \mathrm{y} \in S_{i}, \quad i=1, \cdots, k θx+(1−θ)y∈Si,i=1,⋯,k,因为每一个集合都是凸集,所以连接任意两点的线段都在每一个集合内,因此也就在所有集合的交集内。即: θ x + ( 1 − θ ) y ∈ ∩ i = 1 k S i \theta \mathbf{x}+(1-\theta) \mathbf{y} \in \cap_{i=1}^{k} S_{i} θx+(1−θ)y∈∩i=1kSi,因此凸集的交集还是凸集。
-
凸集的并集不一定是凸集。
-
多面体:有限个半空间和半平面的交集
P = { x ∣ A x ≤ b , C x = d } \mathcal{P}=\{\mathrm{x} | \mathrm{Ax} \leq \mathrm{b}, \mathrm{Cx}=\mathrm{d}\} P={x∣Ax≤b,Cx=d}

原因分析:对于 A x ≤ b \mathrm{Ax} \leq \mathrm{b} Ax≤b,每一行都是一个半空间(凸集),而 A x ≤ b \mathrm{Ax} \leq \mathrm{b} Ax≤b为多个半空间的交集,也是凸集;对于 C x = d \mathrm{Cx}=\mathrm{d} Cx=d每一行都是一个超平面(凸集),多个超平面的交集还是凸集。
2.2 凸函数
2.2.1 凸函数的定义
-
一个函数 f : R n → R f:\mathbf{R}^n \rightarrow \mathbf{R} f:Rn→R被称为凸函数,如果
-
定义域 d o m ( f ) dom(f) dom(f)为凸集
-
对于任何 x , y ∈ d o m ( f ) \mathbf{x,y}\in dom(f) x,y∈dom(f)和 0 ≤ θ ≤ 1 0 \le \theta \le1 0≤θ≤1,有
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f(\theta\mathbf{x}+(1-\theta)\mathbf{y}) \le \theta f(\mathbf{x})+(1-\theta)f(\mathbf{y}) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)

-
-
凸函数的一阶二阶充要条件
- 一阶充要条件(不好用): f ( x 1 ) ≥ f ( x ) + ∇ T f ( x ) ( x 1 − x ) f\left(\mathrm{x}_{1}\right) \geq f(\mathrm{x})+\nabla^{T} f(\mathrm{x})\left(\mathrm{x}_{1}-\mathrm{x}\right) f(x1)≥f(x)+∇Tf(x)(x1−x)对于所有的 x 1 , x \mathbf{x_1,x} x1,x均成立。
- 二阶充要条件:如果函数二阶可导,则凸函数的充要条件: H ( x ) \mathbf{H(x)} H(x)半正定。
2.2.2 常见的凸函数
- 一元函数举例:
- a x + b ax+b ax+b 既凸且凹
- x 2 x^2 x2 凸函数(二阶导数大于0)
- e α x e^{\alpha x} eαx 凸函数(二阶导数: α 2 e α x \alpha^2 e^{\alpha x} α2eαx)
- − l o g x c o n v e x o n x > 0 -log\ x \ convex \ on \ x>0 −log x convex on x>0,二阶导数 1 x 2 \frac{1}{x^2} x21
- x l o g x c o n v e x o n x > 0 xlogx \ convex \ on \ x>0 xlogx convex on x>0,二阶导数 1 x \frac{1}{x} x1
- 二元函数举例
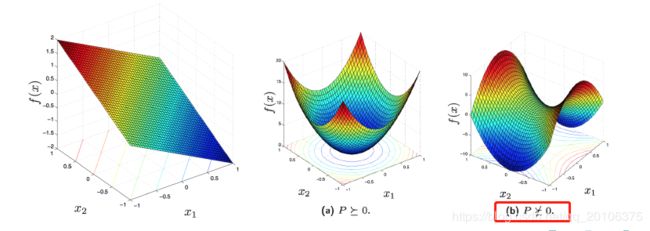
- f ( x ) = a T x + b f\mathbf{(x) = \mathbf{a^Tx+b}} f(x)=aTx+b,既凸且凹。 ∇ f ( x ) = a , ∇ 2 f ( x ) = 0 \nabla f(\mathbf{x})=\mathbf{a},\nabla^2f(\mathbf{x}) = \mathbf{0} ∇f(x)=a,∇2f(x)=0.
- f ( x ) = x T P x + 2 q T x + r f\mathbf{(x) =\mathbf{x^TPx+} 2\mathbf{q^Tx+r}} f(x)=xTPx+2qTx+r, 是凸函数的条件: ∇ 2 f ( x ) = 2 P ≥ 0 \nabla^2f(\mathbf{x}) = 2\mathbf{P}\ge 0 ∇2f(x)=2P≥0,即 P \mathbf{P} P为半正定矩阵。
- f ( x ) = ∣ ∣ x ∣ ∣ 2 2 = x T x f\mathbf{(x)} =||\mathbf{x}||^2_2=\mathbf{x^Tx} f(x)=∣∣x∣∣22=xTx,是凸函数,因为 P = I \mathbf{P=I} P=I是单位阵。
2.2.3 保凸运算
-
f ( x ) f(\mathbf{x}) f(x)凸,则 f ( A x + b ) f(\mathbf{Ax+b}) f(Ax+b)凸。
- 解释: A x + b \mathbf{Ax+b} Ax+b为仿射变换,相当于对原始图像进行了‘线性变换+平移’。并不改变函数的凸性。可以参考《通俗理解仿射变换》。
- 举例: f ( x ) = x 2 f(x)=x^2 f(x)=x2是凸函数, f ( 2 x + 1 ) = ( 2 x + 1 ) 2 f(2x+1)=(2x+1)^2 f(2x+1)=(2x+1)2也是凸函数。
- 这个性质,就可以解释线性回归的损失函数 ∣ ∣ y − X w ∣ ∣ 2 2 ||\mathbf{y-Xw}||_2^2 ∣∣y−Xw∣∣22是凸函数。
-
g凸,h凸,扩展的h非递减,则 f ( x ) = h ( g ( x ) ) f(\mathbf{x})=h(g(\mathbf{x})) f(x)=h(g(x))凸。例如: f ( x ) = ∥ y − A x ∥ 2 2 f(x)=\|y-A x\|_{2}^{2} f(x)=∥y−Ax∥22凸, g ( x ) = ∥ y − A x ∥ 2 g(\mathrm{x})=\|\mathrm{y}-\mathrm{Ax}\|_{2} g(x)=∥y−Ax∥2, h ( x ) = x 2 h(x)=x^{2} h(x)=x2在 x ≥ 0 x \ge0 x≥0部分非递减。
-
f 1 , ⋯ , f m f_{1}, \cdots, f_{m} f1,⋯,fm凸, w 1 , ⋯ , w m ≥ 0 w_{1}, \cdots, w_{m} \geq 0 w1,⋯,wm≥0,则 ∑ i = 1 m w i f i \sum_{i=1}^{m} w_{i} f_{i} ∑i=1mwifi凸,例如: f ( x ) = ∥ y − A x ∥ 2 2 + γ ∥ x ∥ 2 2 f(x)=\|y-A x\|_{2}^{2}+\gamma\|x\|_{2}^{2} f(x)=∥y−Ax∥22+γ∥x∥22凸, γ ≥ 0 \gamma \ge 0 γ≥0.简单来讲:就是凸函数的非负线性组合还是凸函数。
-
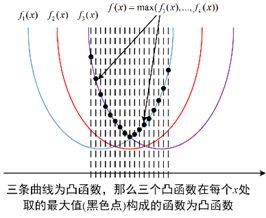
逐点最大: f 1 , ⋯ , f m f_{1}, \cdots, f_{m} f1,⋯,fm凸,则 f ( x ) = max { f 1 ( x ) , ⋯ , f m ( x ) } f(\mathrm{x})=\max \left\{f_{1}(\mathrm{x}), \cdots, f_{m}(\mathrm{x})\right\} f(x)=max{f1(x),⋯,fm(x)}凸。 f ( x , y ) f(\mathrm{x}, \mathrm{y}) f(x,y)对于每个 y ∈ A \mathrm{y} \in \mathcal{A} y∈A凸,则 sup y ∈ A f ( x , y ) \sup _{\mathbf{y} \in \mathcal{A}} f(\mathbf{x}, \mathbf{y}) supy∈Af(x,y)凸。
2.2.4 α \alpha α水平集
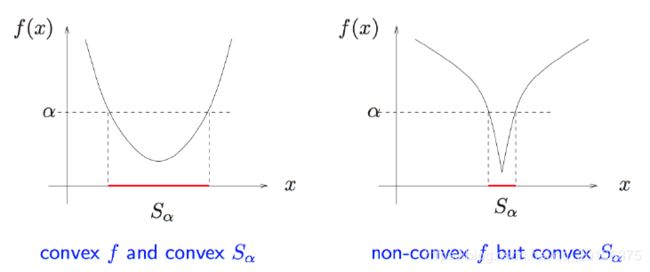
- 一元函数 f f f的 α \alpha α水平集为:
S α = { x ∣ f ( x ) ≤ α } S_{\alpha}=\{x | f(x) \leq \alpha\} Sα={x∣f(x)≤α}
则有 f f f为凸函数 → S α \rightarrow S_\alpha →Sα对于每个 α \alpha α是凸集,反之则不成立。
三:凸优化问题
3.1 凸优化问题说明
-
凸优化问题
m i n m i z e f 0 ( x ) s u b j e c t t o f i ( x ) ≤ 0 f o r i = 1 , 2 , . . . m h i ( x ) = 0 f o r i = 1 , 2 , . . . p minmize\quad f_0(\mathbf{x})\\ subject\ to\ f_i(\mathbf{x})\le0 \quad for\ i = 1,2,...m\\ \quad \quad \quad \quad h_i(\mathbf{x}) = 0\quad for\ i=1,2,...p minmizef0(x)subject to fi(x)≤0for i=1,2,...mhi(x)=0for i=1,2,...p -
目标函数是凸函数,可行域是凸集
- 目标函数是凸函数。
- 不等式约束函数必须是凸的。(则0水平集是凸集)
- 等式约束函数必须是仿射的。(类似 A x = b \mathbf{Ax=b} Ax=b,解为凸集)
-
凸优化问题的本质:在一个凸集上极小化一个凸函数
-
f 0 ( x ∗ ) = p ∗ f_{0}\left(\mathrm{x}^{*}\right)=p * f0(x∗)=p∗
-
凸优化问题的局部最优即为全局最优
3.2 典型的凸优化问题
-
线性规划(Liner Programming;LP)
m i n i m i z e c T x + d s u b j e c t t o G x ≤ h A x = b minimize \quad \mathbf{c}^{T} \mathbf{x}+d\\ subject\ to\ \mathrm{Gx} \leq \mathrm{h}\\ \qquad \qquad \ \mathrm{Ax}=\mathrm{b} minimizecTx+dsubject to Gx≤h Ax=b- 说明:首先目标函数是仿射函数,既是凸函数也是凹函数(二阶导数为0)。 G x ≤ h \mathrm{Gx} \leq \mathrm{h} Gx≤h是一系列半空间的交集(凸集的交集还是凸集),是凸集; A x = b \mathrm{Ax}=\mathrm{b} Ax=b是一系列超平面的交集(凸集的交集还是凸集),凸集。所以可行域为凸集。符合在凸集上极小化一个凸函数。
-
二次规划(Quadratic Programming;QP)( P \mathbf{P} P半正定)
m i n i m i z e 1 2 x T P x + c T x + d s u b j e c t t o G x ≤ h A x = b minimize \frac{1}{2} \mathbf{x}^{T} \mathbf{P} \mathbf{x}+\mathbf{c}^{T} \mathbf{x}+d\\ subject\ to\ \mathbf{Gx} \leq \mathbf{h}\\ \qquad \qquad \ \mathbf{Ax}=\mathbf{b} minimize21xTPx+cTx+dsubject to Gx≤h Ax=b- 说明:目标函数求二阶导可知 ∇ 2 f ( x ) = P ≥ 0 \nabla^2f(\mathbf{x})=\mathbf{P} \ge0 ∇2f(x)=P≥0,即半正定。所以目标函数是一个凸函数。又因为可行域是凸集,所以符合在凸集上极小化一个凸函数。
-
QCQP( P \mathbf{P} P和 Q i \mathbf{Q_i} Qi均半正定):
m i n i m i z e 1 2 x T P x + c T x + d s u b j e c t t o 1 2 x T Q i x + r i T x + s i ≤ 0 ; i = 1 , 2 ⋯ m A x = b minimize \quad \frac{1}{2} \mathbf{x}^{T} \mathbf{P} \mathbf{x}+\mathbf{c}^{T} \mathbf{x}+d\\ subject\ to\qquad \frac{1}{2} \mathbf{x}^{T} \mathbf{Q_i} \mathbf{x}+\mathbf{r_i}^{T} \mathbf{x}+s_i \le0;i=1,2 \cdots m\\ \mathrm{Ax}=\mathrm{b} minimize21xTPx+cTx+dsubject to21xTQix+riTx+si≤0;i=1,2⋯mAx=b- 说明:目标函数为凸函数;可行域中, 1 2 x T Q i x + r i T x + s i ≤ 0 ; i = 1 , 2 ⋯ m \frac{1}{2} \mathbf{x}^{T} \mathbf{Q_i} \mathbf{x}+\mathbf{r_i}^{T} \mathbf{x}+s_i \le0;i=1,2 \cdots m 21xTQix+riTx+si≤0;i=1,2⋯m,可以理解为凸函数的0水平集,还是凸集。
四:普通问题转为凸优化问题(案例演示)
-
给定下列问题:将其转为标准的凸优化问题
m i n i m i z e 1 2 ∥ w ∥ 2 2 + C ∑ i = 1 m ξ i s u b j e c t t o y i ( w T x i + b ) ≥ 1 − ξ i , i = 1 , ⋯ , m ξ i ≥ 0 minimize \ \frac{1}{2}\|\mathbf{w}\|_{2}^{2}+C \sum_{i=1}^{m} \xi_{i}\\ subject \ to \qquad y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right) \geq 1-\xi_{i}, i=1, \cdots, m\\\xi_{i} \geq 0 minimize 21∥w∥22+Ci=1∑mξisubject toyi(wTxi+b)≥1−ξi,i=1,⋯,mξi≥0
其中 w ∈ R n , ξ = [ ξ 1 , ⋯ , ξ m ] T ∈ R m , b ∈ R \mathbf{w} \in \mathbb{R}^{n}, \boldsymbol{\xi}=\left[\xi_{1}, \cdots, \xi_{m}\right]^{T} \in \mathbb{R}^{m}, b \in \mathbb{R} w∈Rn,ξ=[ξ1,⋯,ξm]T∈Rm,b∈R.定义 k = m + n + 1 k=m+n+1 k=m+n+1(未知变量的个数)。说明:未知变量为 w , b , ξ w,b,\xi w,b,ξ。 C , y , x C,y,x C,y,x已知。
转换过程
-
定义变量
x ∈ R k = [ w ξ b ] \mathbf{x} \in \mathbf{R}^{k}=\left[ \begin{array}{l}{\mathbf{w}} \\ {\mathbf{\xi}} \\ {b}\end{array}\right] x∈Rk=⎣⎡wξb⎦⎤X ∈ R m × n = [ x 1 T ⋮ x m T ] , y ∈ R m = [ y 1 ⋮ y m ] \mathbf{X} \in \mathbb{R}^{m \times n}=\left[ \begin{array}{c}{\mathbf{x}_{1}^{T}} \\ {\vdots} \\{\mathbf{x}_{m}^{T}}\end{array}\right], \mathbf{y} \in \mathbb{R}^{m}=\left[ \begin{array}{c}{y_{1}} \\ {\vdots} \\ {y_{m}}\end{array}\right] X∈Rm×n=⎣⎢⎡x1T⋮xmT⎦⎥⎤,y∈Rm=⎣⎢⎡y1⋮ym⎦⎥⎤
-
回归QP问题:
m i n i m i z e 1 2 x T P x + c T x + d s u b j e c t t o G x ≤ h A x = b minimize \frac{1}{2} \mathbf{x}^{T} \mathbf{P} \mathbf{x}+\mathbf{c}^{T} \mathbf{x}+d\\ subject\ to\ \mathbf{Gx} \leq \mathbf{h}\\ \qquad \qquad \ \mathbf{Ax}=\mathbf{b} minimize21xTPx+cTx+dsubject to Gx≤h Ax=b -
定义
P ∈ R k × k = [ I 0 0 0 0 0 0 0 0 ] , c ∈ R k = [ 0 C ⋅ 1 ( v e c t o r ) 0 ] \mathbf{P} \in \mathbb{R}^{k \times k}=\left[ \begin{array}{lll}{\mathbf{I}} & {0} & {0} \\ {0} & {0} & {0} \\ {0} & {0} & {0}\end{array}\right], \mathbf{c} \in \mathbb{R}^{k}=\left[ \begin{array}{c}{0} \\ {C \cdot \mathbf{1(vector)}} \\ {0}\end{array}\right] P∈Rk×k=⎣⎡I00000000⎦⎤,c∈Rk=⎣⎡0C⋅1(vector)0⎦⎤
G ∈ R 2 m × k = [ − diag ( y ) X − I − y 0 − I 0 ] , h ∈ R 2 m = [ − 1 ( v e c t o r ) 0 ( v e c t o r ) ] \mathbf{G} \in \mathbb{R}^{2 m \times k}=\left[ \begin{array}{ccc}{-\operatorname{diag}(\mathbf{y}) \mathbf{X}} & {-\mathbf{I}} & {-\mathbf{y}} \\ {0} & {-\mathbf{I}} & {0}\end{array}\right], \mathbf{h} \in \mathbb{R}^{2 m}=\left[ \begin{array}{c}\mathbf{-1(vector)} \\ \mathbf{0(vector)}\end{array}\right] G∈R2m×k=[−diag(y)X0−I−I−y0],h∈R2m=[−1(vector)0(vector)]
则
1 2 x T P x = 1 2 [ w T , ξ T , b T ] [ I 0 0 0 0 0 0 0 0 ] [ w ξ b ] = 1 2 [ w T , ξ T , b T ] [ w 0 0 ] = 1 2 ∥ w ∥ 2 2 \frac{1}{2} \mathbf{x}^{T} \mathbf{P} \mathbf{x}= \frac{1}{2} \left[\mathbf{w}^T,\mathbf{\xi}^T, {b}^T\right]\left[ \begin{array}{lll}{\mathbf{I}} & {0} & {0} \\ {0} & {0} & {0} \\ {0} & {0} & {0}\end{array}\right] \left[ \begin{array}{l}{\mathbf{w}} \\ {\mathbf{\xi}} \\ {b}\end{array}\right]=\frac{1}{2} \left[\mathbf{w}^T,\mathbf{\xi}^T, {b}^T\right]\left[ \begin{array}{l}{\mathbf{w}} \\ {0} \\ {0}\end{array}\right]=\frac{1}{2}\|\mathbf{w}\|_{2}^{2} 21xTPx=21[wT,ξT,bT]⎣⎡I00000000⎦⎤⎣⎡wξb⎦⎤=21[wT,ξT,bT]⎣⎡w00⎦⎤=21∥w∥22
c T x = [ 0 , C 1 T , 0 ] [ w ξ b ] = C ∑ i = 1 m ξ i \mathbf{c}^{T} \mathbf{x}=\left[0,C\mathbf{1}^T, {0}\right]\left[ \begin{array}{l}{\mathbf{w}} \\ {\mathbf{\xi}} \\ {b}\end{array}\right]=C \sum_{i=1}^{m} \xi_{i} cTx=[0,C1T,0]⎣⎡wξb⎦⎤=Ci=1∑mξi
G x = [ − diag ( y ) X − I − y 0 − I 0 ] [ w ξ b ] = [ − diag ( y ) X w − ξ − b y − ξ ] ≤ [ − 1 0 ] → [ diag ( y ) X w + b y ≥ 1 − ξ ξ ≥ 0 ] → y i ( w T x i + b ) ≥ 1 − ξ i , i = 1 , ⋯ , m ξ i ≥ 0 \mathbf{Gx}=\left[ \begin{array}{ccc}{-\operatorname{diag}(\mathbf{y}) \mathbf{X}} & {-\mathbf{I}} & {-\mathbf{y}} \\ {0} & {-\mathbf{I}} & {0}\end{array}\right]\left[ \begin{array}{l}{\mathbf{w}} \\ {\mathbf{\xi}} \\ {b}\end{array}\right]=\left[ \begin{array}{ccc}{-\operatorname{diag}(\mathbf{y}) \mathbf{Xw}-\mathbf{\xi}-b\mathbf{y}} \\ {-\mathbf{\xi}} \end{array}\right] \\ \le\left[ \begin{array}{c}\mathbf{-1} \\ \mathbf{0}\end{array}\right]\rightarrow \left[ \begin{array}{ccc}{\operatorname{diag}(\mathbf{y}) \mathbf{Xw}+b\mathbf{y}}\ge \mathbf{1-\xi} \\ {\mathbf{\xi}}\ge0 \end{array}\right]\\ \rightarrow y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right) \geq 1-\xi_{i}, i=1, \cdots, m\\\xi_{i} \geq 0 Gx=[−diag(y)X0−I−I−y0]⎣⎡wξb⎦⎤=[−diag(y)Xw−ξ−by−ξ]≤[−10]→[diag(y)Xw+by≥1−ξξ≥0]→yi(wTxi+b)≥1−ξi,i=1,⋯,mξi≥0
- 经过上述推导,可以发现原问题转换为了一个QP问题,是一个凸优化问题。而对于凸优化问题,目前已经有非常成熟的解决办法了。因此,能够将一个问题转换为凸优化问题是最为重要的一步。
五:参考资料
- https://www.cnblogs.com/hgl0417/p/6670762.html
- https://www.matongxue.com/madocs/244.html