4.弹性网络（ Elastic Net）

ElasticNet 是一种使用L1和L2先验作为正则化矩阵的线性回归模型.这种组合用于只有很少的权重非零的稀疏模型，比如:class:Lasso, 但是又能保持:class:Ridge 的正则化属性.我们可以使用 l1_ratio 参数来调节L1和L2的凸组合(一类特殊的线性组合)。
当多个特征和另一个特征相关的时候弹性网络非常有用。Lasso 倾向于随机选择其中一个，而弹性网络更倾向于选择两个.
在实践中，Lasso 和 Ridge 之间权衡的一个优势是它允许在循环过程（Under rotate）中继承 Ridge 的稳定性.
弹性网络的目标函数是最小化:
minw12nsamples||Xw−y||22+αρ||w||1+α(1−ρ)2||w||22
ElasticNetCV 可以通过交叉验证来用来设置参数 α(α) 和 l1ratio(ρ)

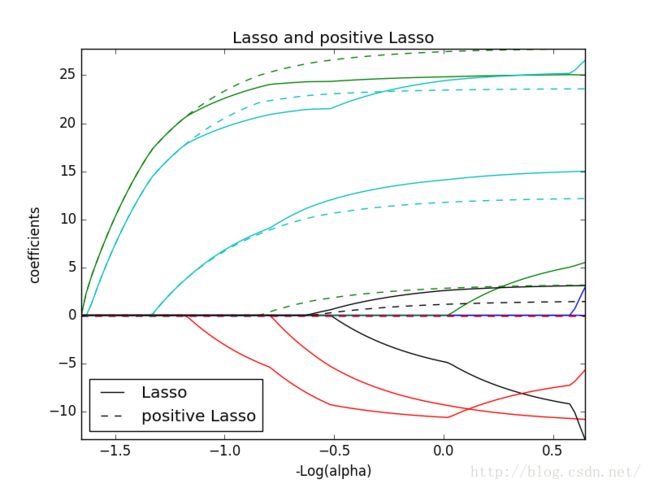
print(__doc__)

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import lasso_path, enet_path
from sklearn import datasets

diabetes = datasets.load_diabetes()
X = diabetes.data
y = diabetes.target

X /= X.std(axis=0)  # Standardize data (easier to set the l1_ratio parameter)

# Compute paths

eps = 5e-3  # the smaller it is the longer is the path

print("Computing regularization path using the lasso...")
alphas_lasso, coefs_lasso, _ = lasso_path(X, y, eps, fit_intercept=False)

print("Computing regularization path using the positive lasso...")
alphas_positive_lasso, coefs_positive_lasso, _ = lasso_path(
    X, y, eps, positive=True, fit_intercept=False)
print("Computing regularization path using the elastic net...")
alphas_enet, coefs_enet, _ = enet_path(
    X, y, eps=eps, l1_ratio=0.8, fit_intercept=False)

print("Computing regularization path using the positve elastic net...")
alphas_positive_enet, coefs_positive_enet, _ = enet_path(
    X, y, eps=eps, l1_ratio=0.8, positive=True, fit_intercept=False)

# Display results

plt.figure(1)
ax = plt.gca()
ax.set_color_cycle(2 * ['b', 'r', 'g', 'c', 'k'])
l1 = plt.plot(-np.log10(alphas_lasso), coefs_lasso.T)
l2 = plt.plot(-np.log10(alphas_enet), coefs_enet.T, linestyle='--')

plt.xlabel('-Log(alpha)')
plt.ylabel('coefficients')
plt.title('Lasso and Elastic-Net Paths')
plt.legend((l1[-1], l2[-1]), ('Lasso', 'Elastic-Net'), loc='lower left')
plt.axis('tight')


plt.figure(2)
ax = plt.gca()
ax.set_color_cycle(2 * ['b', 'r', 'g', 'c', 'k'])
l1 = plt.plot(-np.log10(alphas_lasso), coefs_lasso.T)
l2 = plt.plot(-np.log10(alphas_positive_lasso), coefs_positive_lasso.T,
              linestyle='--')

plt.xlabel('-Log(alpha)')
plt.ylabel('coefficients')
plt.title('Lasso and positive Lasso')
plt.legend((l1[-1], l2[-1]), ('Lasso', 'positive Lasso'), loc='lower left')
plt.axis('tight')


plt.figure(3)
ax = plt.gca()
ax.set_color_cycle(2 * ['b', 'r', 'g', 'c', 'k'])
l1 = plt.plot(-np.log10(alphas_enet), coefs_enet.T)
l2 = plt.plot(-np.log10(alphas_positive_enet), coefs_positive_enet.T,
              linestyle='--')

plt.xlabel('-Log(alpha)')
plt.ylabel('coefficients')
plt.title('Elastic-Net and positive Elastic-Net')
plt.legend((l1[-1], l2[-1]), ('Elastic-Net', 'positive Elastic-Net'),
           loc='lower left')
plt.axis('tight')
plt.show()