向量的基本运算
向量是什么
向量就是给定一个点A,连接原点到点A,并具有由O到A方向的连线,表示为 O A ⃗ \vec{OA} OA. 书本的定义:向量就是具有大小和方向东西。
大小(magnitude)
向量的大小(magnitude)写作 ∥ x ∥ \Vert x \Vert ∥x∥,称为模(norm).
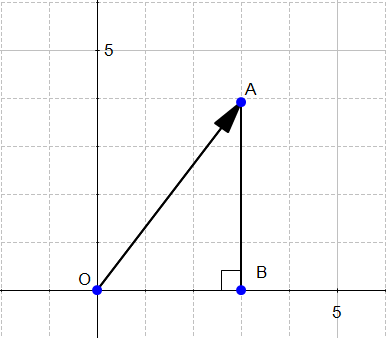
通过(Pythagoras’ theorem)毕达哥拉斯定理求模如下图,
O A 2 = O B 2 + A B 2 {OA}^2 = {OB}^2 + {AB}^2 OA2=OB2+AB2
O A 2 = 3 2 + 4 2 {OA}^2 = {3}^2 + {4}^2 OA2=32+42
∥ x ∥ = 5 \Vert x \Vert = 5 ∥x∥=5
方向(direction)
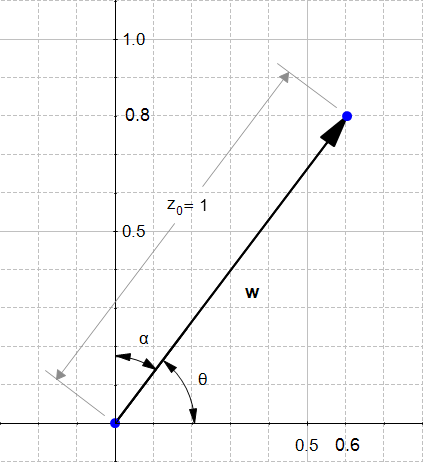
定义向量 u ( u 1 , u 2 ) \mathbf{u} (u_1,u_2) u(u1,u2)的方向为向量 w ( u 1 ∥ u ∥ , u 2 ∥ u ∥ ) \mathbf{w}(\frac{u_1}{\|u\|}, \frac{u_2}{\|u\|}) w(∥u∥u1,∥u∥u2)。如下图:
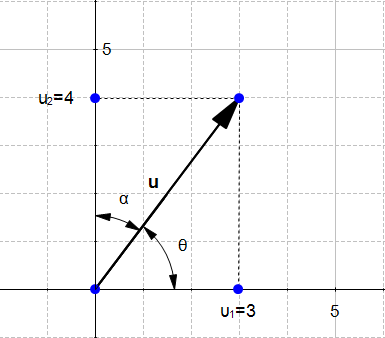
可以看到:
c o s ( θ ) = u 1 ∥ u ∥ cos(\theta)=\frac{u_1}{\|u\|} cos(θ)=∥u∥u1
c o s ( α ) = u 2 ∥ u ∥ cos(\alpha)=\frac{u_2}{\|u\|} cos(α)=∥u∥u2
所以向量 u ( 3 , 4 ) \mathbf{u}(3,4) u(3,4)方向向量是 w ( 0.6 , 0.8 ) \mathbf{w}(0.6,0.8) w(0.6,0.8)。方向向量的模为1.如下图
两个向量的加法
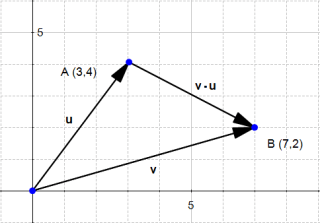
任意给给两个向量 u ( u 1 , u 2 ) \mathbf{u} (u_1, u_2) u(u1,u2) , v ( v 1 , v 2 ) \mathbf{v} (v_1, v_2) v(v1,v2)两个向量相加: u + v = ( u 1 + v 1 , u 2 + v 2 ) \mathbf{u}+\mathbf{v}= (u_1+v_1, u_2+v_2) u+v=(u1+v1,u2+v2)
两个向量的减法
任意给给两个向量 u ( u 1 , u 2 ) \mathbf{u} (u_1, u_2) u(u1,u2) , v ( v 1 , v 2 ) \mathbf{v} (v_1, v_2) v(v1,v2)两个向量相减: u − v = ( u 1 − v 1 , u 2 − v 2 ) \mathbf{u}-\mathbf{v}= (u_1-v_1, u_2-v_2) u−v=(u1−v1,u2−v2)。 方向指向被减数的方向。
向量的点积(dot product)
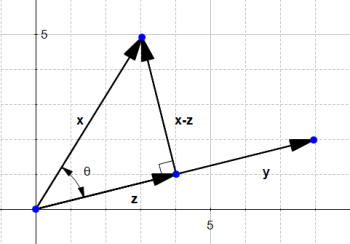
x ⋅ y = ∥ x ∥ ∥ y ∥ c o s ( θ ) \mathbf{x} \cdot \mathbf{y} = \|x\| \|y\|cos(\theta) x⋅y=∥x∥∥y∥cos(θ), θ \theta θ 为两个向量的夹角。
推导过程如下:
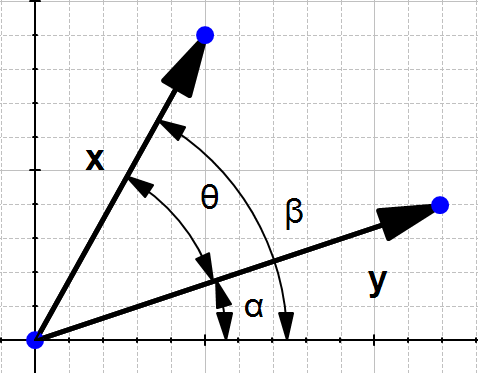
根据前面的分析我们知道,
c o s ( β ) = a d j a c e n t h y p o t e n u s e = x 1 ∥ x ∥ cos(\beta) =\frac{adjacent}{hypotenuse} =\frac{x_1}{\|x\|} cos(β)=hypotenuseadjacent=∥x∥x1
s i n ( β ) = o p p o s i t e h y p o t e n u s e = x 2 ∥ x ∥ sin(\beta) =\frac{opposite}{hypotenuse} =\frac{x_2}{\|x\|} sin(β)=hypotenuseopposite=∥x∥x2
c o s ( α ) = a d j a c e n t h y p o t e n u s e = y 1 ∥ y ∥ cos(\alpha) =\frac{adjacent}{hypotenuse} =\frac{y_1}{\|y\|} cos(α)=hypotenuseadjacent=∥y∥y1
s i n ( α ) = o p p o s i t e h y p o t e n u s e = y 2 ∥ y ∥ sin(\alpha) =\frac{opposite}{hypotenuse} = \frac{y_2}{\|y\|} sin(α)=hypotenuseopposite=∥y∥y2
从图片中得到 θ = β − α \theta = \beta - \alpha θ=β−α, 那么 c o s ( θ ) = c o s ( β − α ) cos(\theta) = cos(\beta - \alpha) cos(θ)=cos(β−α)
c o s ( β − α ) = c o s ( β ) c o s ( α ) + s i n ( β ) s i n ( α ) cos(\beta - \alpha) = cos(\beta)cos(\alpha) + sin(\beta)sin(\alpha) cos(β−α)=cos(β)cos(α)+sin(β)sin(α)
于是,
c o s ( θ ) = c o s ( β − α ) = c o s ( β ) c o s ( α ) + s i n ( β ) s i n ( α ) cos(\theta) = cos(\beta - \alpha) = cos(\beta)cos(\alpha) + sin(\beta)sin(\alpha) cos(θ)=cos(β−α)=cos(β)cos(α)+sin(β)sin(α)
c o s ( θ ) = x 1 ∥ x ∥ y 1 ∥ y ∥ + x 2 ∥ x ∥ y 2 ∥ y ∥ cos(\theta) = \frac{x_1}{\|x\|}\frac{y_1}{\|y\|}+ \frac{x_2}{\|x\|}\frac{y_2}{\|y\|} cos(θ)=∥x∥x1∥y∥y1+∥x∥x2∥y∥y2
c o s ( θ ) = x 1 y 1 + x 2 y 2 ∥ x ∥ ∥ y ∥ cos(\theta) = \frac{x_1y_1 + x_2y_2}{\|x\|\|y\|} cos(θ)=∥x∥∥y∥x1y1+x2y2
∥ x ∥ ∥ y ∥ c o s ( θ ) = x 1 y 1 + x 2 y 2 \|x\|\|y\|cos(\theta) = x_1y_1 + x_2y_2 ∥x∥∥y∥cos(θ)=x1y1+x2y2
点积的算术定义就出来,
x ⋅ y = x 1 y 1 + x 2 y 2 = ∑ i = 1 2 ( x i y i ) \mathbf{x} \cdot \mathbf{y} =x_1y_1 + x_2y_2 = \sum_{i=1}^{2}(x_iy_i) x⋅y=x1y1+x2y2=i=1∑2(xiyi)
从上面的集合定义也能知道,两个向量的点积是一个数。
向量的正交投影
如图给定两个向量x,y,那么向量x在y上的投影为z。
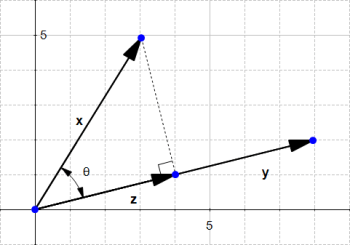
通过上面的学习我们知道,
c o s ( θ ) = ∥ z ∥ ∥ x ∥ cos(\theta)= \frac{\|z\|}{\|x\|} cos(θ)=∥x∥∥z∥
∥ z ∥ = ∥ x ∥ c o s ( θ ) \|z\|=\|x\|cos(\theta) ∥z∥=∥x∥cos(θ)
点积 c o s ( θ ) = x ⋅ y ∥ x ∥ ∥ y ∥ cos(\theta) = \frac{\mathbf{x} \cdot \mathbf{y}}{\|x\|\|y\|} cos(θ)=∥x∥∥y∥x⋅y
于是可以推导得
∥ z ∥ = x ⋅ y ∥ y ∥ \|z\|=\frac{\mathbf{x} \cdot \mathbf{y}}{\|y\|} ∥z∥=∥y∥x⋅y
另外我们知道方向向量的,如果u表示向量y的方向向量, u = y ∥ y ∥ \mathbf{u}=\frac{\mathbf{y}}{\|y\|} u=∥y∥y, 那么向量x在向量y上面的投影可以由下式计算:
∥ z ∥ = u ⋅ x \|z\|=\mathbf{u} \cdot \mathbf{x} ∥z∥=u⋅x
我们还注意到,向量x在向量y上的投影得到的向量z,它的方向向量和向量y的方向向量是一致的,所以向量z可表示为 z = ∥ z ∥ u \mathbf{z}=\|z\|\mathbf{u} z=∥z∥u。
知道了向量x在向量y上面的投影z后,我们就能够计算向量x-z的距离:
∥ x − z ∥ = ( 3 − 4 ) 2 + ( 5 − 1 ) 2 = 17 \|x-z\| = \sqrt{(3-4)^2 + (5-1)^2}=\sqrt{17} ∥x−z∥=(3−4)2+(5−1)2=17
详见原文地址:https://www.svm-tutorial.com/2014/11/svm-understanding-math-part-2/