炼丹-深度学习-《Deep Residual Learning for Image Recognition》

Deep Residual Learning for Image Recognition

原文地址：Deep Residual Learning for Image Recognition

生词：

单词	释义
popularize	使受欢迎，使通俗化
envelop	掩盖，遮住
obstacle	障碍
reformulate	重新定制
Solely	仅仅;纯粹;
hamper	阻碍
degradation	恶化，毁坏
counterpart	相当的人
feasible	可行的，可能的
asymptotically	渐进的
counterintuitive	反直觉的；有悖常理的
precondition	先决条件；前提
perturbation	扰动
conjecture	尚不确定；推测

Abstract

作者提出这个模型的初衷：太深的模型太难训练了，所以作者提出了一种残差(residual)的方式去缓解deeper的模型难以训练的问题。

作者主要做了以下几类实验：

（1）作者用了一个152层的网络，在imagent上获得了3.57%的错误。这个准确率赢得了ILSVRC 2015 classification task比赛的第一名。

（2）作者也分析了从几十层到100层再到1000层的网络在CIFAR-10数据集上的效果。

（3）在COCO物体检测数据集上获得了28%的提升。

在ImageNet detection, ImageNet local- ization, COCO detection, and COCO segmentation都获得了第一的名次

Introduction

以往的实验表明，越深的模型拥有越好的性能。那么就产生一个问题：是不是只要堆叠模型的深度就能使得模型的性能越来越好呢？一个显著的问题就是梯度消失和梯度爆炸。这个问题已经被模型参数的归一初始化和中间层的归一化方法给解决了。

虽然梯度消失和梯度爆炸的问题解决了，但是还有个问题：***degradation(模型退化)***，这个问题的表现是这样的：虽然模型的深度增加，但当模型的性能趋于饱和时（例如准确率不再上升），最终模型的性能相较于浅层的版本却有了很大的降低，表现就是在训练集、测试集、验证集上都比不上浅层版本模型训练的效果。而且很不幸的是，这个问题不是overfitting，并且越是增加模型层数，效果会越差。

作者通过浅层网络+y=x等同映射构造深层模型，结果深层模型并没有比浅层网络有等同或更低的错误率，推断退化问题可能是因为深层的网络并不是那么好训练，也就是求解器很难去利用多层网络拟合同等函数。（这个实验我先这么理解一下：应该就是在一个shallower的已经训练好的网络中，附加一些层，这层主要是为了学习同等映射，这样相当于增加了模型的深度，而模型的表现又不变差，作者想通过这个实验说明：理论来说，增加模型深度最坏的情况下也应该能学习到很浅层模型相当的表现效果，不应该会更差，所以判断退化可能是因为模型优化做的不够好）

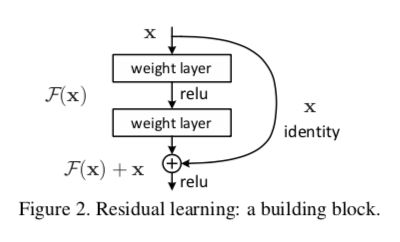
假设我们潜在的优化目标为：H(x)，我们让网络去预测另一个东西：F(x) = H(x) - x，那么原始的H(x)就可以表示为F(X) + x。作者假设F(X)会比H(x)更好优化。因为即使在最极端的情况下，也可以让F(X)拟合为0，F(X)=H(x)。这样就相当于在增加模型深度的情况下，也不会使得模型退化。

这样的shortcut connections如下：

这样的模型既不会增加额外的参数，也没有额外的计算开销，可以很容易的被一般的gd，例如SGD等实现。

本文通过在imagenet上的实现证明了两件事：

• 模型容易优化
• 通过增加深度可以显著的看到模型准确率的提升

Deep Residual Learning

Residual Learning

这个残差学习基于的假设是这样的：如果一个多层的非线性网络的输出可以逐渐优化逼近一个函数H(x)，那么它一定也可以逼近H(x)-x。这两者优化的区别会有很大的不同。

按照introduction部分提到的实验：如果通过叠加部分层的同等映射来增加网络的深度，网络最后的映射结果应该是不会变的，所以一个模型如果深度增加了，理论上来讲最差的情况应该也和它的浅层版本效果持平（简单的把额外的层优化成同等映射）。然而实际学习过程中却遇到了模型退化(degradation)的问题，说明多层的非线性层很难做到同等映射。面对这个问题，如果通过残差学习的方式，可以通过使得输出为0（这很简单，只要让权重都为0就可以）来让层与层之间学习同等映射。

Identity Mapping by Shortcuts

$$y=F(x,w_i)+x$$

上面的F就是正常多层线性网络的输出，x就是最上层添加的输入。

但是这样的结构必须保证输入和输出是同一个纬度的，所以一般会在input上面加上一个线性的变换：

$$y=F(x,w_i)+W_{s}x$$

F的形式在实际应用中是有很多变体的，例如可以在层数上变化，一层、两层、三层等等。可以在形式上变化，例如全连阶层、卷积层。

Network Architecture

作者通过对照组实验来说明residual的优越性，分别用了两个结构的模型：plain network和residual network

Plain Network

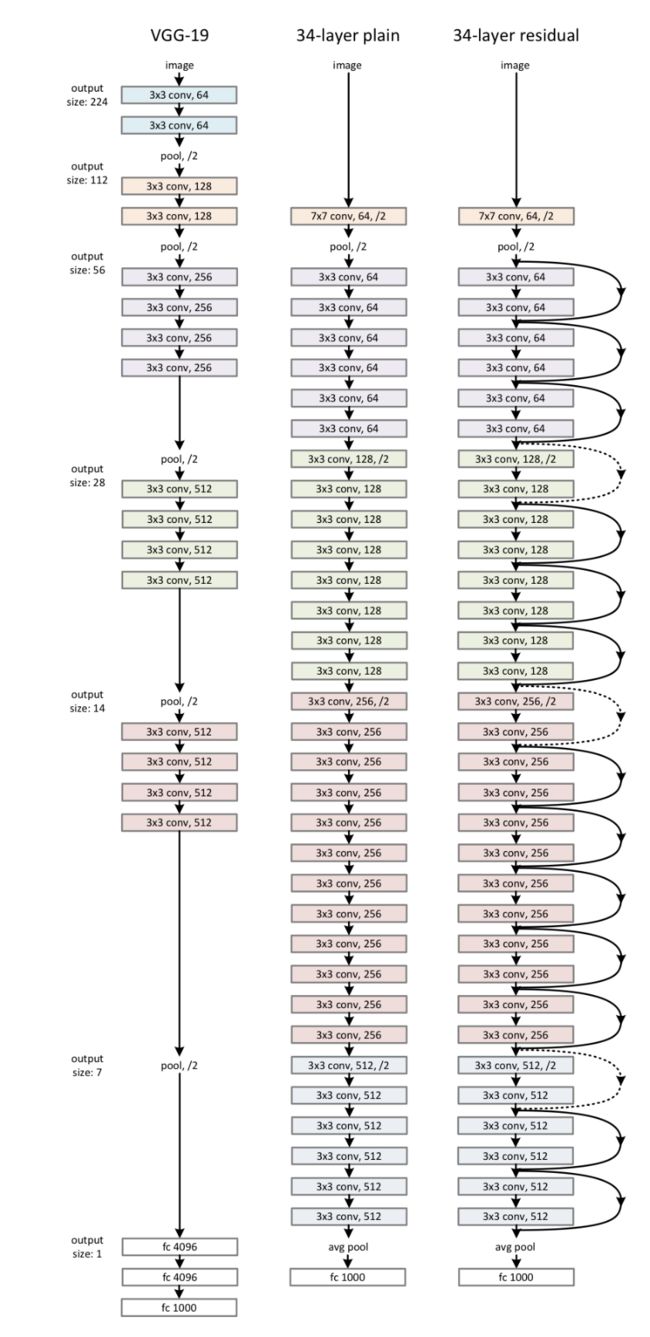
Plain NetWork是上图中间的网络，基于VGG的灵感来设计的，主要基于以下两个设计原则：

• 对于输出的size不变的卷积层，其filter的个数和输入的channel个数一致
• 对于输出的size减少一倍的卷积层，其filter的个数是输入channel的两倍

Residual Network

Shortcut Connections有两种：

• 如果输入和输出的维度是一致的，直接相加即可
• 如果输出的维度比输入有增加，则要么做zero padding，要么做一个1*1的卷积

这一段如果难懂，可以看下原文，以下是原文部分。

When the dimensions increase (dotted line shortcuts in Fig. 3), we consider two options: (A) The shortcut still performs identity mapping, with extra zero entries padded for increasing dimensions. This option introduces no extra parameter; (B) The projection shortcut in Eqn.(2) is used to match dimensions (done by 1×1 convolutions). For both options, when the shortcuts go across feature maps of two sizes, they are performed with a stride of 2

Implementation

这一段是作者的实现细节，包括数据增强和实验参数的设定，直接看原文，不再赘述

Our implementation for ImageNet follows the practice in [21, 41]. The image is resized with its shorter side ran- domly sampled in [256, 480] for scale augmentation [41].
A 224×224 crop is randomly sampled from an image or its horizontal flip, with the per-pixel mean subtracted [21]. The standard color augmentation in [21] is used. We adopt batch normalization (BN) [16] right after each convolution and before activation, following [16]. We initialize the weights as in [13] and train all plain/residual nets from scratch. We use SGD with a mini-batch size of 256. The learning rate starts from 0.1 and is divided by 10 when the error plateaus, and the models are trained for up to 60 × 104iterations. We use a weight decay of 0.0001 and a momentum of 0.9. We do not use dropout [14], following the practice in [16].
In testing, for comparison studies we adopt the standard 10-crop testing [21]. For best results, we adopt the fully- convolutional form as in [41, 13], and average the scores at multiple scales (images are resized such that the shorter side is in {224, 256, 384, 480, 640}).

Experiment

ImageNet Classification

作者在ImageNet上检验了模型的有效性

• 类别：1000
• 训练集：128w
• 验证集：5w
• 测试集：10w
• 评估指标：top1和top5准确率

下面两张图分别是实验的结果以及训练过程中损失的变化曲线

plain net

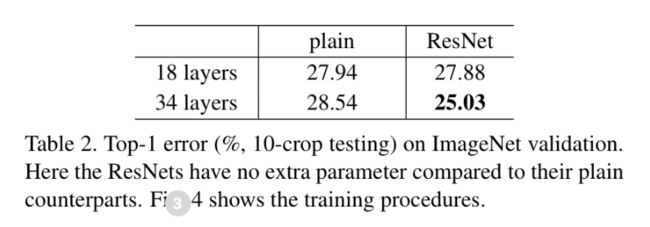
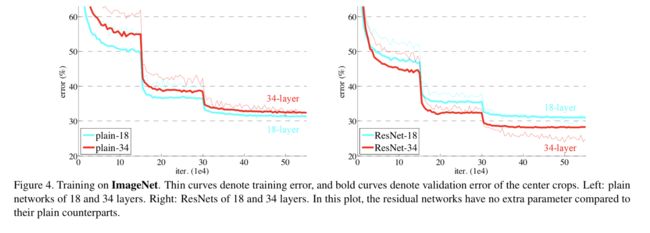
作者对比了一个18层和34层的plain net，发现在验证集的准确率上，18层plain net高于34层的plain net，在训练集的错误率上，34层的更高一点。

作者排除了是梯度消失的问题，因为在网络层中加入了batch normalization，而且就实验结果来看，34层的结果虽然比18层的差，但也比较有效，所以排除了梯度消失问题。而且同时在训练集和验证集上都比18层的差，也排除了过拟合的问题。但作者也不排除一种可能性：深层的模型需要更长的时间去收敛

residual net

最后的实验结果告诉我们三个结论：

• 从结果图可以看出，34层的residual net不管是在训练集合还是验证集合的表现上，都优于18层的residual net，说明residual有效的解决了模型退化的问题。
• 34层的residual net比34层的plain net好很多，说明了残差网络在深度模型上的有效性。
• 18层的residual/net虽然最终达到的准确率相当，但是residual的收敛速度很快，说明residual结构能在模型训练早期提供更快的收敛速度。

Identity vs. Projection Shortcuts

上面两者结果的对比中，residual net里面的shortcut在维度变化的情况下，是用的zero padding，相当于没有增加任何模型的参数和额外计算量。作者还对比了通过Projection来做变换的shortcuts。

在这部分实验里，作者比较了以下三种shortcuts:

• (option A) zero padding的shortcuts
• (option B) 对应dimensions增加的用projections shortcuts，没有增加的用identity shortcuts
• (option C) 所有的shortcuts都是projections

从表格数据来看，有以下几个结论：

• residual比plain的好，无论是A,B,C。
• B比A好，表明zero-padding可能没有residual learning。
• C比B好，我们归功于projections引入了更多的学习参数。
• A/B/C虽然一步一步的提高了效果，但是变化不大，说明projections没有从本质上解决模型退化问题（实际是residual本身解决了）。

Deeper Bottleneck Architectures

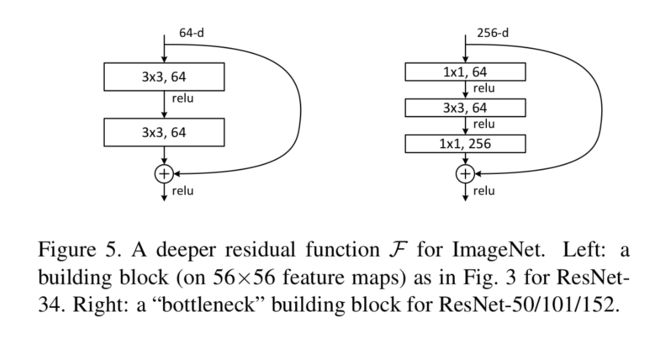
由于gpu和时间的限制，作者修改了block的结构为bottleneck block。其结构图如下：

首先解释一下bottleneck的结构：bottleneck首先通过11的卷积给原来的feature map降维，再经过一个33的卷积，再经过一个1*1的卷积来升维。这个经典的结构基于的理论是：高维的特征具有更多的可区分性(具体在哪篇文章看到的得找找啊)。通过这种方式，在不增加模型复杂度的情况下，提升了特征的维度。

作者在这里陈述了一个观点，但是我觉得很奇怪：作者在这里想表述的是，identity shortcuts对于bottleneck的结构是非常重要的，因为如果bottleneck的结构用到projection shortcuts的话，由于输入输出的维度很高，会产生比用于一般block的projection shortcuts更加多的参数，所以如果在bottleneck中用projections shortcuts是不现实的，所以identity shortcuts对于bottleneck architecture尤其重要。。。。

50-layer ResNet

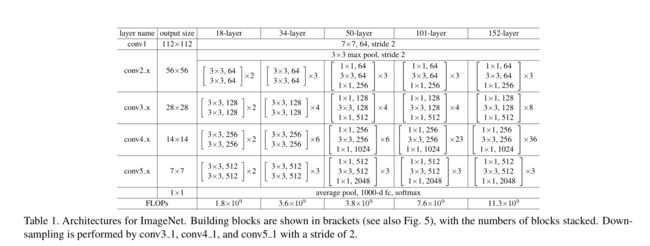
作者替换了2-layer block为3-block的bottleneck architecture，具体的细节如上，总的计算量为3.8 billion FLOPS。

101-layer and 152-layer ResNets

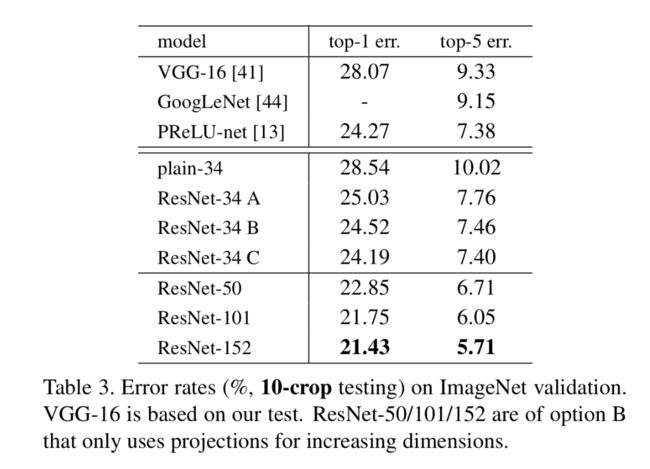
作者通过增加更多的bottleneck来增加网络深度，发现在152-layer的时候，其计算量还是比VGG低，并且随着深度的增加，也没有遇到模型退化的问题。具体结果可以看以下两个表格：

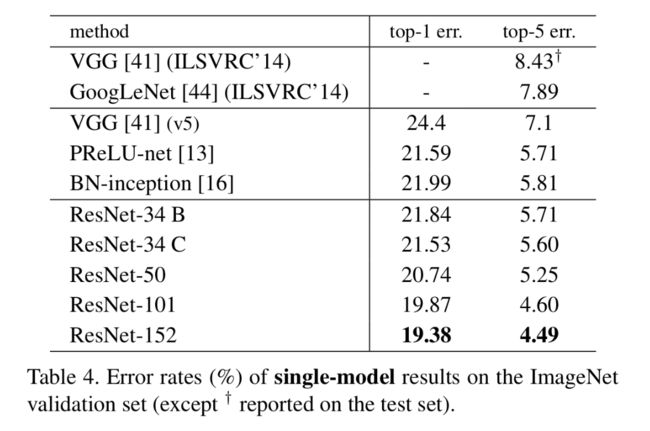
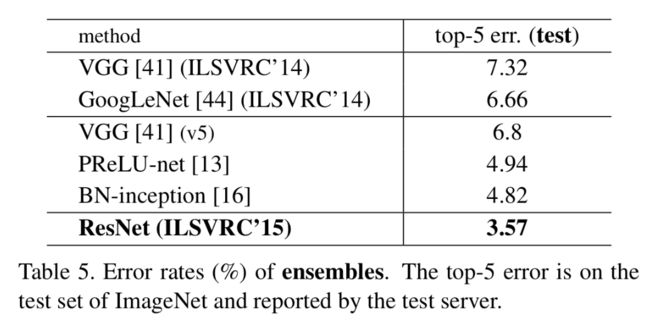
Comparisons with State-of-the-art Methods

作者用一个152-layer的single residual net就达到了超过其他ensemble网络的准确率，当作者融合了六种不通深度的网络后，其准确率更是达到了更大的提升，具体可以看Table4和Table5。

CIFAR-10 and Analysis

作者在CIFAR-10上面做了更进一步的实验分析。

• 训练集：50k
• 测试集：10k
• 类别：10
• 目的：实验的目的不是拿sota，而是研究深度带来的优越性，所以用的是简单网络。

实验结果的细节不叙述了，总的来说，作者得到了这几个结论：

• 随着深度的增加，residual net不会遇到模型退化问题，而plain net很容易就遇到模型退化问题。
• 随着深度的增加，residual net的收敛会变得比较难，所以需要在初始的时候调小学习率来收敛，然后再增加学习率来快速收敛，最后慢慢减小学习率。
• 随着深度的增加，residual网络越往后面的filter的参数其std越接近于0（相比较plain net而言，虽然都在减小，但是residual net更加明显），验证了作者开头的假设。
• 随着深度进一步的增加，如果1202层，residual net依旧不会面临模型退化问题的，在训练集上拟合的非常好，但在验证集和测试集会变差，显然是overfit的文婷。作者提出可能可以通过一些正则化的手段来提升。

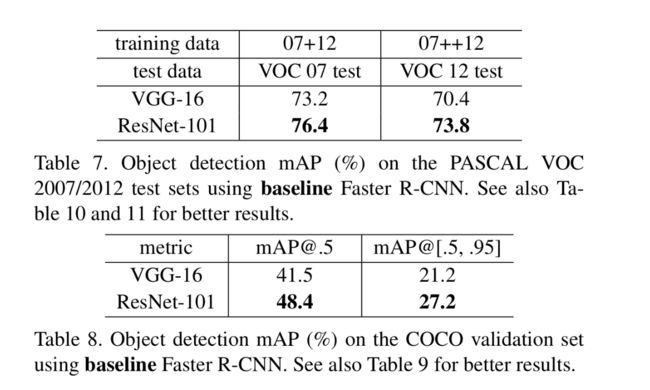
Object Detection on PASCAL and MS COCO

这里作者几乎一段带过，列了两个表说明了resnet在物体检测上的成果。