cs231n作业,assignment1-knn详解(注重算法与代码的结合)
作业下载地址
建议作业完成顺序
- k近邻分类:knn.ipynb & k_nearest_neighbor.py
- svm线性分类:svm.ipynb & linear_svm.py & linear_classifier.py
- softmax线性分类:softmax.ipynb & softmax.py
- 两层神经网络:two_layer_net.ipynb & neural_net.py
文章目录
- k近邻分类算法介绍
- k_nearest_neighbor.py
- 1.记住所有训练图像
- 2. 计算测试图像与所有训练图像的l2距离
- 2.1 双重循环
- 2.2 单重循环实现
- 2.3 向量化(不使用循环)
- broadcast简介
- 3. 预测标签
- knn.ipynb (解决k取值问题)
k近邻分类算法介绍
- 记住所有训练图像
- 计算测试图像与所有训练图像的距离(常用l2距离)
- 选择与测试图像距离最小的k张训练图像
- 计算这k张图像所对应的类别出现的次数,选择出现次数最多的类别记为预测类别
k_nearest_neighbor.py
首先定义一个k近邻分类器的类
class KNearestNeighbor(object):
""" 一个使用L2距离的KNN线性分类器 """
def __init__(self):
pass
1.记住所有训练图像
self.X_train 是训练数据,维度是 (N,D),训练集有N个样本,每个样本特征是D维
self.y_train 是标签,维度是(N,),即N个训练样本对应的标签
def train(self, X, y):
"""
训练分类器,但是对应于k近邻,就是记住训练数据
输入:
- X: 训练集,维度 (num_train, D),num_train个样本,每个样本维度为D
- y: 训练集的标签,维度 (N,) y[i]是X[i]的标签.
"""
self.X_train = X
self.y_train = y
预测时首先计算测试样本与所有训练样本的距离
计算距离提供了三种方法,分别为需要三重循环,双重循环,不需要循环
然后根据距离判断样本的类别
def predict(self, X, k=1, num_loops=0):
"""
使用这个分类器预测测试数据的标签
Inputs:
- X: A numpy array of shape (num_test, D) containing test data consisting
of num_test samples each of dimension D.
- k: The number of nearest neighbors that vote for the predicted labels.
- num_loops: Determines which implementation to use to compute distances
between training points and testing points.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
if num_loops == 0:
dists = self.compute_distances_no_loops(X)
elif num_loops == 1:
dists = self.compute_distances_one_loop(X)
elif num_loops == 2:
dists = self.compute_distances_two_loops(X)
else:
raise ValueError('Invalid value %d for num_loops' % num_loops)
return self.predict_labels(dists, k=k)
2. 计算测试图像与所有训练图像的l2距离
2.1 双重循环
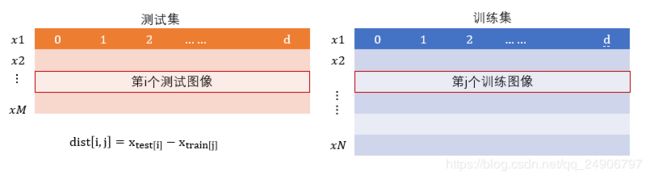
第i个测试样本与第j个训练样本的距离 d i s t [ i , j ] dist[i,j] dist[i,j]等于用第i个测试图像的特征向量对应维度得知,减去第j个训练图像的特征向量的值
∑ d d i s t [ i , j ] = ( x t e s t [ i , d ] − x t r a i n [ j , d ] ) 2 \sqrt{\sum_d{dist[i,j]={(x_{test[i,d]}-x_{train[j,d]})}^2}} d∑dist[i,j]=(xtest[i,d]−xtrain[j,d])2
在python中两个维度相同的向量可以直接相减 dists[i,j] = np.sqrt(np.sum(np.square(X[i]-self.X_train[j])))
def compute_distances_two_loops(self, X):
"""
计算测试图像X与训练图像的距离
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: dists[i, j]存储第i张测试图像与第j张训练图像的距离
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
for j in range(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension, nor use np.linalg.norm(). #
#####################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists[i,j] = np.sqrt(np.sum(np.square(X[i]-self.X_train[j])))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists
2.2 单重循环实现
通过使用numpy的broadcast机制,可以直接计算第i张测试图像与所有训练样本的距离
第i张测试图像 x t e s t [ i , : ] x_{test}[i,:] xtest[i,:]的维度[1,d],所有训练样本 x t r a i n x_{train} xtrain的维度(N,d),
dists[i,:] = np.sqrt((np.sum(np.square(X[i,:]-self.X_train),axis=1)))

def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
# Do not use np.linalg.norm(). #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists[i,:] = np.sqrt((np.sum(np.square(X[i,:]-self.X_train),axis=1)))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists
2.3 向量化(不使用循环)
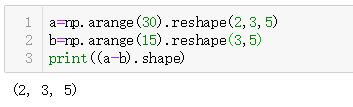
直接用 x t e s t − x t r a i n x_{test}-x_{train} xtest−xtrain 会报错

broadcast简介
所以说broadcast也不是无条件随便两个矩阵都能广播的,这里就需要了解一下广播的条件:
两个numpy数组,维度从后往前比较,如果满足以下两个条件就可以广播
两个矩阵不能直接相减,怎么才能不用循环计算距离? ( a − b ) 2 = a 2 + b 2 − 2 a b (a-b)^2=a^2+b^2-2ab (a−b)2=a2+b2−2ab
dists = np.sqrt(-2*np.dot(X, self.X_train.T) + np.sum(np.square(self.X_train), axis = 1) + np.transpose([np.sum(np.square(X), axis = 1)]))
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy, #
# nor use np.linalg.norm(). #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists = np.sqrt(-2*np.dot(X, self.X_train.T) + np.sum(np.square(self.X_train), axis = 1) + np.transpose([np.sum(np.square(X), axis = 1)]))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists
3. 预测标签
-
选择与测试图像最相似(距离最小)的k张训练图像
np.argsort(dists[i])函数是将dist中的i行元素从小到大排列,并得到对应的index,
然后取前k个索引(也就是得到距离最近的k张图像的索引) -
计算这k张图像所对应的类别出现的次数,选择出现次数最多的类别记为预测类别
现在要统计这k个值哪个值出现的次数多。
一开始是想建立一个字典,但是没想到有np.bincount()这个函数可以统计数组中的数字出现的次数。
简单介绍一下np.bincount():
x = np.array([0, 1, 1, 3, 2, 1, 7]) #x中最大值为7,索引值即为0->7,bin是8个
np.bincount(x)
#x中索引0出现了1次,索引1出现了3次......索引5出现了0次......
#因此,输出结果为:array([1, 3, 1, 1, 0, 0, 0, 1])
def predict_labels(self, dists, k=1):
"""
Given a matrix of distances between test points and training points,
predict a label for each test point.
Inputs:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
gives the distance betwen the ith test point and the jth training point.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
num_test = dists.shape[0]
y_pred = np.zeros(num_test)
for i in range(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
closest_y = []
#########################################################################
# TODO: #
# Use the distance matrix to find the k nearest neighbors of the ith #
# testing point, and use self.y_train to find the labels of these #
# neighbors. Store these labels in closest_y. #
# Hint: Look up the function numpy.argsort. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#closest_y = self.y_train[np.argsort(dists, axis=1)[:,:k]]
closest_y = self.y_train[np.argsort(dists[i])[:k]]
# *****END OF YOUR CODE (DO NOT[ DELETE/MODIFY THIS LINE)*****
#########################################################################
# TODO: #
# Now that you have found the labels of the k nearest neighbors, you #
# need to find the most common label in the list closest_y of labels. #
# Store this label in y_pred[i]. Break ties by choosing the smaller #
# label. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
y_pred[i] = np.argmax(np.bincount(closest_y))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return y_pred
knn.ipynb (解决k取值问题)
knn需要选择k个近邻然后进行t投票,那么问题来了,k应该取几效果会比较好呢?
- 划分训练集
- 交叉验证
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#将数据集划分为n份
X_train_folds=np.array_split(X_train,num_folds)
y_train_folds=np.array_split(y_train,num_folds)
#print(np.array(X_train_folds).shape,np.array(y_train_folds).shape)#(5, 1000, 3072) (5, 1000)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#这里参数k指代的不是k折交叉验证,而是k近邻中的k选择多少合适
for k in k_choices:
k_to_accuracies.setdefault(k, [])
for i in range(num_folds):
classifier = KNearestNeighbor()
X_val_train = np.vstack(X_train_folds[0:i] + X_train_folds[i+1:])
y_val_train = np.hstack(y_train_folds[0:i] + y_train_folds[i+1:])
classifier.train(X_val_train, y_val_train)
for k in k_choices:
y_val_pred = classifier.predict(X_train_folds[i], k)
num_correct = np.sum(y_val_pred == y_train_folds[i])
accuracy = float(num_correct) / len(y_val_pred)
k_to_accuracies[k] += [accuracy]
#rint(k_to_accuracies[k])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))